Sean \(\Pi\) un plano afín, \(f \in \text{Aut}(\Pi)\) y \(\overline{\Pi}\) el plano proyectivo en el cual se sumerge \(\Pi\text{,}\) entonces existe única \(\overline{f} \in \text{Aut}(\overline{\Pi}) \) tal que \(\overline{f}|_{\Pi}=f\text{.}\)
Sea \(\Pi= (\mathcal{P},\mathcal{L}, \mathcal{I})\) plano afín y \(\overline{\Pi}= (\overline{\mathcal{P}},\overline{\mathcal{L}}, \overline{\mathcal{I}})\) el correspondiente plano proyectivo y \(f \in \text{Aut}(\Pi)\text{.}\)
Sean \(l,m\in \mathcal{L}\text{,}\) sabemos que si \(m \parallel l\text{,}\) entonces \(f(m) \parallel f(l)\text{.}\) Por lo anterior tenemos que esta bien definida
Luego definimos \(\overline{f}(P)=f(P)\text{,}\) con \(P\in \mathcal{P}\) y con ello tenemos
en donde
Veamos en las rectas, sea \(l\in \mathcal{L}\text{,}\) luego tenemos que
de donde obtenemos
Ambas son biyectivas y respetan incidencia.
Sea \(\mathcal{A}\) un plano afín, Entonces existe un único plano proyectivo \(\Pi\) tal que \(\mathcal{A}\) es isomorfo a \(\Pi^l\) para alguna recta \(l\in \Pi\text{.}\)
Por la sección anteriores tenemos la constricción del plano proyectivo y al considerar la recta \(l=l_\infty\) obtenemos lo pedido.
Dos planos afines \(\Pi^l\) y \(\Pi'^m\) son isomorfos (existe una colineación) si y sólo si existe un isomorfismo (colineación) entre los planos proyectivos \(\Pi\) y \(\Pi'\text{,}\) de modo que envía \(l\) en \(m\text{.}\)
Sea \(\theta:\Pi^l\rightarrow \Pi'^m \) un isomorfismo o colineación de planos afines.
Construimos la \(\psi :\Pi\rightarrow \Pi' \text{,}\) del siguiente modo
Sea \(P\in \mathcal{P}\text{,}\) si \(P\not\mathcal{I} l\text{,}\) luego \(\psi(P)=\theta(P)\)
En caso contrario, sea \(h\) otra recta tal que \(P\mathcal{I}h\text{,}\) notemos que todas las recta que inciden en \(P\) tiene un único punto en común, \(\psi(P) = \theta(h)\cap m\text{,}\) con ello esta bien definida en los puntos y es biyectiva.
Sea \(h\in \mathcal{L}\text{,}\) luego \(\psi(h)= \theta(h)\) para todo \(h\neq l\text{,}\) y en el otro caso \(\psi(l)=m\text{.}\)
Corresponde a una isomorfismo, que preserva incidencia por construcción.
Inversamente supongamos que \(\psi :\Pi\rightarrow \Pi'\) es un isomorfismo de plano proyectivo. tal que \(\psi(l)=m\text{.}\)
Claramente la restricción es una función biyectiva entre los puntos y las rectas de cada uno de los planos afines.
La función \(\psi\) preserva incidencia, luego la restricción también, por ultimo dada dos rectas paralelas \(h,k \in \Pi^l\text{,}\) significa que el punto de intersección pertenece a \(l\text{,}\) por ello, el punto de intersección \(\psi(h), \psi(k)\) pertenece a \(m\) y por ende son paralelas en \(\Pi'^m\text{.}\)
Sabemos que las dilataciones un plano afín son de dos tipos homotecia y traslaciones, aplicando el teorema anterior veamos como se extiende estas dilataciones.
Sea \(\overline{\Pi}\) el plano proyectivo en el que esta sumergido \(\Pi\) plano afín y \(f\) una homotecia en \(\Pi\text{.}\)
Determinar los puntos fijos y las rectas fijas de \(\overline{f}\text{.}\)
Sea \(P\) el punto fijo por la homotecia \(f\text{,}\) además para todo \(l \in \mathcal{L}\) entonces \(f(l) \parallel l\text{,}\) de lo cual se obtiene que
Luego todos los haces de rectas están fijas por \(\overline{f}\text{.}\) Es decir, \(\overline{f}\) fija \(P\) y todas las haces de rectas paralelas \([l]\text{.}\) Así tenemos que \(\overline{f}(l_\infty)=l_\infty\text{.}\)
Finalmente, sea \(l \in \mathcal{L}\text{,}\) tal que \(P \ \mathcal{I} \ l\text{,}\) luego \(P \ \mathcal{I} \ f(l)\) y \(f(l) \parallel l\text{,}\) por axioma del plano afín \(f(l)=l\text{.}\)
De este modo tenemos que \(\overline{f}\) fija \(l_\infty\) y toda recta \(l \in \overline{\mathcal{L}}\) tal que \(P \ \mathcal{I} \ l \text{.}\)
Sea \(\overline{\Pi}\) el plano proyectivo en el que esta sumergido \(\Pi\) plano afín y \(t\) una traslación en \(\Pi\text{.}\)
Determinar los puntos fijos y rectas fijas de \(\overline{t}\text{.}\)
Análogamente a lo anterior, tenemos que:
luego los únicos puntos fijos de \(\overline{t}\) son los haces de rectas.
Además \(\overline{t}\) fija las mismas rectas que fija \(t\) incluyendo \(l_\infty\text{.}\)
Sea \(\mathbb{K}\) un cuerpo y \(\Pi\) el plano Afín Vectorial \(\mathbb{K}^2\) y \(\overline{\Pi}= \mathbb{P}_2 (\mathbb{K}^3)\) el Plano Proyectivo Vectorial donde esta sumergido \(\Pi\text{.}\)
Dada la traslación \(t(x)= \overrightarrow{x}+ \overrightarrow{w}\) en \(\Pi\text{,}\) explicitar \(\overline{t}\)
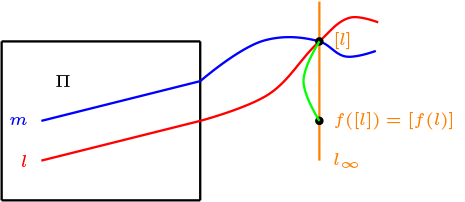
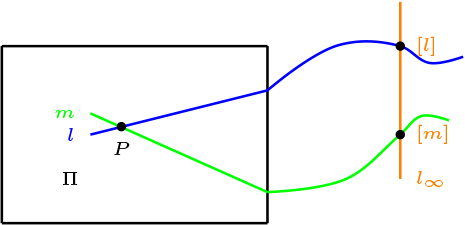
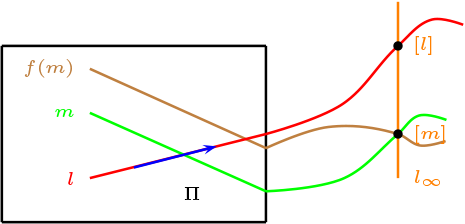
Sea \(t(x,y)= (x+a,y+b)\text{,}\) la traslación dada y definimos
Trasladando a \(\Pi_1\) obtenemos
Dada la recta que pasa por los puntos \((c,d), (u,v)\text{,}\) luego la recta que une los puntos en forma vectorial es \(l= \lt c-u,d-v\gt +(u,v)\text{,}\) y el correspondiente representante en plano \(\Pi_0\) es
De esta manera tenemos que la recta que pasa por \(t(c,d), t(u,v)\text{,}\) esta dada por
la representante en plano \(\Pi_0\) es \(l'= \lt c-u,d-v,0)\gt \)
extendiendo linealmente los elementos de la recta, obtenemos que \(\overline{t}(x,y,z)= (\alpha x +az, \beta y+bz, \gamma z)\text{,}\) que al restringir tenemos que \(\overline{t}|_\Pi =t\text{,}\) luego
En las condiciones del ejemplo anterior.
Determinar los puntos y rectas fijas si existen en el plano proyectivo
Sea \(\mathbb{K}\) un cuerpo y \(\Pi\) el plano Afín Vectorial \(\mathbb{K}^2\) y \(\overline{\Pi}= \mathbb{P}_2 (\mathbb{K}^3)\) el Plano Proyectivo Vectorial donde esta sumergido \(\Pi\text{.}\)
Dada la homotecia \(h(\overrightarrow{x})= \alpha \overrightarrow{x}+ (1-\alpha) \overrightarrow{w}\) en \(\Pi\text{,}\) explicitar \(\overline{h}\)
Sea \(h(x,y)= (\alpha x+(1-\alpha) a,\alpha y+(1-\alpha)b)\text{,}\) la homotecia dada y definimos
Trasladando obtenemos
Dada la recta que pasa por los puntos \((c,d), (u,v)\text{,}\) el representante en el plano \(\Pi_0\) es
De esta manera tenemos que, la recta que pasa por \(h(c,d), h(u,v)\text{,}\) esta definida por
el representante en el plano \(\Pi_0\) es \(l'= \lt \alpha(c-u),\alpha(d-v),0)\gt \)
de lo anterior y teniendo presente que debe cumplir que al restringir \(\overline{t}|_\Pi =t\text{,}\) se obtiene
En las condiciones del ejemplo anterior.
Determinar los puntos y rectas fijas si existen en el plano proyectivo
