Observación 2.1.1
Por el axioma uno, dos rectas distintas inciden solamente en un punto.
Sean \(l,m \in \mathcal{L}\) distintas entonces \(l\cap m=\{P\}\text{.}\)
En esta sección abodaremos el concepto de plano proyectivo, y construiremos los planos proyectivos que se obtiene a partir de espacios vectoriales de dimensión tres.
Un estructura de incidencia \(\Pi=(\mathcal{P},\mathcal{L},\mathcal{I})\text{,}\) se dice que \(\Pi\) es un plano proyectivo si y sólo si cumple los siguientes axiomas
Sean \(A,B \in \mathcal{P}\text{,}\) con \(A \neq B\) entonces \(\exists ! l \in \mathcal{L}\) tal que \(A \mathcal{I} l\) y \(B \mathcal{I} l\)
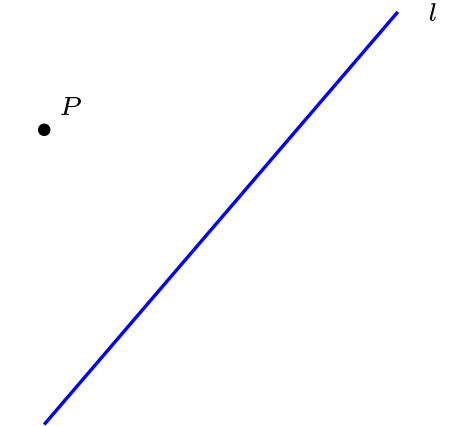
Sean \(l,m \in \mathcal{L}\text{,}\) con \(l \neq m \text{ entonces } l \cap m \neq \varnothing \) (no existen rectas paralelas).
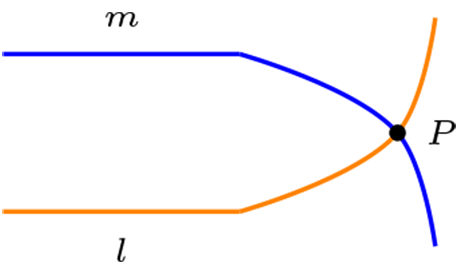
En el plano proyectivo existen un cuadrilátero o cuadrángulo, es decir, no existen tres puntos que pertenezca a la misma recta y toda recta al menos tiene tres puntos distintos.
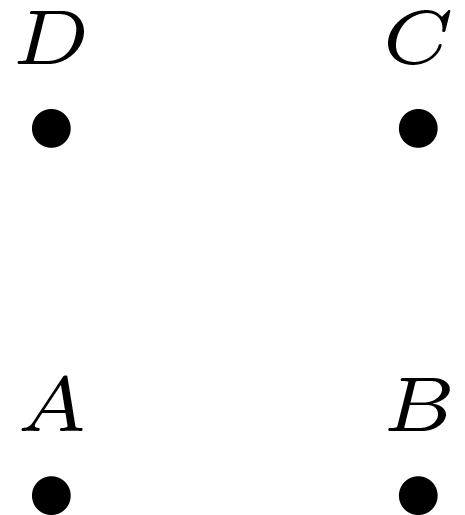
Por el axioma uno, dos rectas distintas inciden solamente en un punto.
Sean \(l,m \in \mathcal{L}\) distintas entonces \(l\cap m=\{P\}\text{.}\)
Todo conjunto de puntos que incide con una misma recta, se llaman puntos colineales.
Todo conjunto de rectas que pasan o inciden en un punto común se llaman rectas concurrentes o coincidentes.
Un conjunto de 3 puntos distintos no colineales \(A,B,C\) junto con las rectas \(l_{BC}, l_{CA} , l_{AB}\) de llama triángulo.
Un conjunto de 4 puntos distintos, 3 de ellos no colineales junto con las rectas de llama cuadrilátero.
Plano Proyectivo minimal es aquel plano proyectivo formado por el menor número de puntos y rectas que cumple con los axioma de plano proyectivo.
Todo plano proyectivo contiene al menos siete puntos.
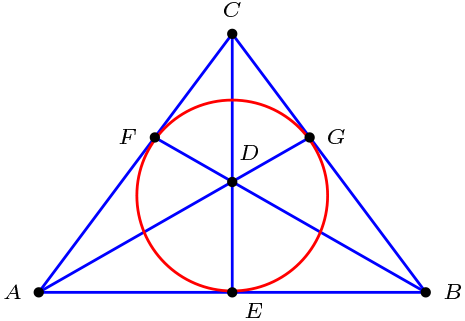
Por axioma tres, sabemos que existen cuatro puntos que denotaremos por \(A, \ B, \ C \text{ y } D \)
\(l_{AB} \cap l_{CD}=\{ E \}\text{,}\) entonces \(E \ \mathcal{I} \ l_{AB}\) y \(E \ \mathcal{I} \ l_{CD}\)
\(l_{AC} \cap l_{BD}=\{ F \}\text{,}\) entonces \(F \ \mathcal{I} \ l_{AC}\) y \(F \ \mathcal{I} \ l_{BD}\)
\(l_{AD} \cap l_{BC}=\{ G \}\text{,}\) entonces \(G \ \mathcal{I} \ l_{AD}\) y \(G \ \mathcal{I} \ l_{BC}\)
Note que, si \(E=F, \ E \ \mathcal{I} \ l_{AB}; \ E \ \mathcal{I} \ l_{AC};\) lo que \(l_{AE}=l_{AB}=l_{AC}\text{;}\) lo que significa que tres puntos son colineales, lo cual no es posible, luego existe siete puntos y al menos siete rectas.
Uno de los ejemplos de plano proyectivo son los que se obtienen a través de los espacios vectoriales de dimension tres
Sea \(V\) un espacio vectorial de dimension tres sobre \(\mathbb{K}\text{.}\)
Se define el conjunto de los puntos y de las rectas por:
y la incidencia la contención.
Sea \(V=\mathbb{Z}_{2} \times \mathbb{Z}_{2}\times \mathbb{Z}_{2}\) \((dim(V)=3)\text{.}\)
Note que cada recta vectorial tiene dos puntos y los planos tiene cuatro puntos incluido el vector nulo.

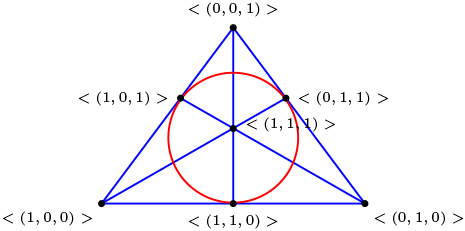
Puntos
Rectas
Luego tenemos que \(\mathbb{Z}_{2} \times \mathbb{Z}_{2}\times \mathbb{Z}_{2}\) es un modelo el plano proyectivo minimal.
En general, con las notaciones anteriores se define el plano proyectivo asociado al espacio vectorial a
Sea \(V\) un espacio vectorial de dimension 3 sobre \(\mathbb{K}\text{,}\) entonces \(\mathbb{P}_{2}(V)\) es un plano proyectivo.
Axioma uno: Por dos puntos distintos pasa una única recta
Sea \(A \neq B\) con \(A=\left\langle \overrightarrow{v}\right\rangle \) y \(B=\left\langle \overrightarrow{w}\right\rangle \text{,}\) entonces \(\{\overrightarrow{v},\overrightarrow{w}\}\) son linealmente independiente, en particular:
Es única, ya que \(A\mathcal{I}m \) y \(B\mathcal{I}m\text{,}\) entonces \(\overrightarrow{v},\overrightarrow{w}\in m\text{,}\) de lo cual obtenemos
como la dimension es dos, se obtiene la igualdad.
Axioma dos: Si \(l \neq m \) entonces \(l \cap m \neq \varnothing\)
Sean \(l=\left\langle \overrightarrow{v},\overrightarrow{w}\right\rangle \) y \(m=\left\langle \overrightarrow{y},\overrightarrow{z}\right\rangle \) con \(l \neq m\text{,}\) entonces \(l+m=V\)
En particular \(l \cap m \neq \varnothing\)
Axioma tres: Existe un cuadrángulo.
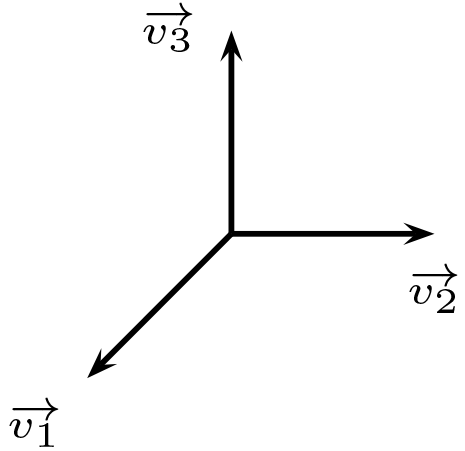
Sea \(B=\{\overrightarrow{v_{1}},\overrightarrow{v_{2}},\overrightarrow{v_{3}}\}\) base de \(V\text{.}\) En donde \(\{\overrightarrow{v_{1}},\overrightarrow{v_{2}},\overrightarrow{v_{3}},\overrightarrow{v_{1}}+\overrightarrow{v_{2}}+\overrightarrow{v_{3}}\}\) forman un cuadrángulo. Ya que dado tres vectores cualquiera, estos son linealmente independientes, luego no hay tres colineales
Por lo tanto \(\mathbb{P}_{2}(V)\) es un plano proyectivo.
Sea \(V\) un \(\mathbb{K}-\)espacio vectorial de dimension tres y \(\mathbb{P}_2(V)\) el plano proyectivo construido a partir de \(V\) con \(P\mathcal{I}l \text{ entonces } P\subseteq l\text{,}\) gráficamente se tiene que:
Sea \(l=\left\langle \overrightarrow{v},\overrightarrow{w}\right\rangle\) recta del plano proyectivo \(\mathbb{P}_2(V)\text{,}\) entonces la ecuación cartesiana de \(l\) con respecto a la base \(B=\{v_1,\ v_2,\ v_3\}\) de \(V\text{,}\) tiene la forma:
con \((a,b,c)\neq (0,0,0)\text{.}\)
Dado los puntos del plano \(A=\left\langle (1,2,4)\right\rangle\) y \(B=\left\langle (-2,1,5)\right\rangle\) en el plano proyectivo \(\mathbb{P}_2(\mathbb{R}^3)\text{.}\)
Determine la ecuación cartesiana de \(l_{AB}\)
Sea \(l_{AB}=\left\langle (1,2,4),(-2,1,5)\right\rangle\text{.}\)
Dado \((x,y,z)\in l_{AB}\) entonces:
El sistema tiene solución si y sólo si
o bien
De otro modo los vectores los vectores \(\{(x,y,z),(1,2,4),(-2,1,5)\}\) son linealmente dependiente, de lo cual tenemos que
En el plano proyectivo \(\mathbb{P}_{2}(\mathbb{Z}_{3}^3)\text{.}\)
Sean \(l_{1}=\left\langle (\overline{1},\overline{2},\overline{0}),(\overline{0},\overline{1},\overline{1}) \right\rangle\) y \(l_{2}\) de ecuación \(\overline{2}x+\overline{3}y-z=0\text{.}\)
Calcule \(l_{1} \cap l_{2}\)
Sea \((x,y,z) \in l_{1}\cap l_{2} \text{,}\) por pertenecer a la primera recta \(l_1\) tenemos:
Como también \((x,y,z) \in l_2\text{,}\) satisface la ecuación, reemplazando tenemos que
luego
Por lo tanto \(l_1 \cap l_2 = \left\{ \left\langle (1,1,2)\right\rangle\right\}\text{.}\)
En el plano proyectivo, todas las rectas tienen el mismo número de puntos.
Sean \(l,m \in \mathcal{L}, l \neq m \) entonces \(l\cap m = \{X \}\) y \(A \in \mathcal{P}\) con \(A \ \not\mathcal{I} \ m \text{ y } A \ \not\mathcal{I} \ l\text{.}\)
Sea \(Z \ \mathcal{I} \ m\text{,}\) luego \(l_{ZA} \cap l=\{ Z' \}\text{.}\)
Construimos una función biyectiva
Con lo cual se obtiene que:
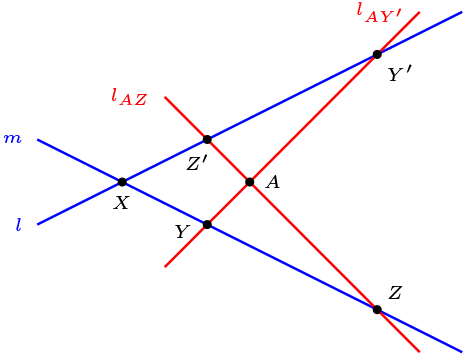
De la misma forma, por cada punto pasa la misma cantidad de rectas.
Sea \(P\in \mathcal{P}\) y \(l\in \mathcal{L}\text{,}\) tal que \(P\not\mathcal{I} l\text{.}\)
Notemos que toda recta que pasa por \(P\) tiene intersección con \(l\) y dado un punto en \(Q\mathcal{I}l\) existe la recta \(l_{PQ}\text{.}\)
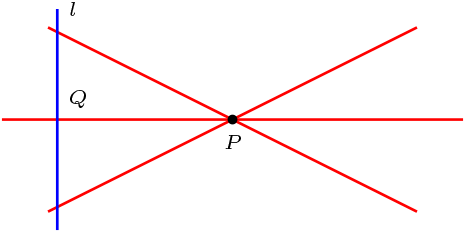
Se dice que el orden del plano proyectivo \(\Pi\) es \(n\) si y sólo si cada recta contiene \(n+1\) puntos, en cuyo caso denotamos por \(\# \Pi=n\text{.}\)
\(\mathbb{P}_{2}(\mathbb{Z}_{2}^3)\) plano proyectivo minimal.
Como cada recta contiene tres puntos, entonces \(\#(\mathbb{P}_{2}(\mathbb{Z}_{2}^3))=2\text{.}\)
En general, si \(\mathbb{K}\) es cuerpo finito entonces \(\#(\mathbb{P}_{2}(\mathbb{K}^3))=|\mathbb{K}|\text{,}\) ya que el plano \(\mathbb{K}^2\text{,}\) por el argumento de la pendiente contiene \(|\mathbb{K}|+1\) rectas vectoriales.
Sea \(\Pi\) tiene un plano proyectivo de orden \(n\text{,}\) entonces
Si \(\Pi\) tiene orden \(n\text{,}\) entonces cada recta contiene \(n+1\) punto y por cada punto \(P\) pasan \(n+1\) rectas.
Dado que por un punto \(P\) pasa \(n+1\) recta y cualquier punto \(Q\) distinto de \(P\) esta contenido en una recta que pasa por \(P\text{,}\) luego tenemos \((n+1)^2\) pero el punto \(P\) lo hemos contado \(n+1\) ya que pertenece a todas las rectas y debemos contarlo una vez.
Dada dos rectas distintas tiene intersección en un punto, y por cada punto pasa \(n+1\) rectas, luego la cantidad de recta es igual al numero de puntos de una recta por la cantidad de recta que pasa por ese punto, teniendo presente que la recta original, se contó tanta vez como punto tiene la recta, por ello

Calcular el \(\# \mathcal{P} \text{ y } \# \mathcal{L}\) de \(\mathbb{P}_{2}(\mathbb{K}^{3})\text{,}\) \(\mathbb{K}\) cuerpo finito.
El orden de \(\mathbb{P}_{2}(\mathbb{K}^{3})\) es \(|\mathbb{K}|\text{.}\) luego tenemos
Para \(\mathbb{K}= \mathbb{Z}_{p}\) se tiene
Si \(n\equiv 1 \mod 4\) o bien \(n \equiv 2 \mod 4\text{,}\) entonces no existe un plano proyectivo de orden \(n\text{,}\) salvo que \(n\) se escriba como suma de dos cuadrados enteros.
\(n=6\text{,}\) no es suma de dos cuadrados enteros y \(n\equiv 2 \mod 4\text{,}\) luego no existe un plano proyectivo de orden \(6\text{,}\) en cambio \(10 = 3^2+1^2 \) y \(10 \equiv 2 \mod 4\text{.}\)
No existe un plano proyectivo de orden \(10\text{.}\)
Un sub-plano \(\Pi_0\) de \(\Pi\text{,}\) es un subconjunto de los elementos de \(\Pi\) que forman un plano proyectivo, teniendo la misma relación de incidencia, es decir, si \(\Pi=(\mathcal{P},\mathcal{L}, \mathcal{I})\) es un plano proyectivo entonces \(\Pi_0=(\mathcal{P}',\mathcal{L}', \mathcal{I})\) es un sub-plano de \(\Pi\) si y sólo si \(\mathcal{P}' \subseteq \mathcal{P}\text{,}\) \(\mathcal{L}' \subseteq \mathcal{L}\) y \(\Pi_0\) es un plano proyectivo
Además es sub-plano es propio si y sólo si \(\Pi_0\neq \Pi\text{.}\)
Como \(\mathbb{R}\) es un subcuerpo de \(\mathbb{C}\text{,}\) tenemos que \(\mathbb{P}_{2}(\mathbb{R}^{3})\) es un sub-plano propio de \(\mathbb{P}_{2}(\mathbb{C}^{3}).\)
Dado una elemento \(v \in\mathbb{R}^{3}\) no nulo, tenemos las rectas \(\lt v\gt \leq \mathbb{R}^{3} \subseteq \mathbb{C}^{3}\text{,}\) aún mas
donde
Notemos que la recta
que corresponde a los puntos del plano proyectivo.
Análogamente para los planos.
En general, si \(\mathbb{F}\) es un subcuerpo de \(\mathbb{K}\) entonces tenemos que \(\mathbb{P}_{2}(\mathbb{F}^{3})\) es un sub-plano de \(\mathbb{P}_{2}(\mathbb{K}^{3})\text{.}\)
Sea \(\Pi\) un plano proyectivo de orden \(n\) y \(\Pi_0\) un sub-plano propio de orden \(m\text{,}\) entonces
Sea \(l\) un recta de \(\Pi_0\text{,}\) luego tiene \(n-m >0\) puntos de \(\mathcal{P}-\mathcal{P}'\text{.}\) Además \(\mathcal{L}'\) contiene \(m^2+m+1\) elementos
De lo anterior tenemos que existen al menos \((n-m)(m^2+m+1)\) puntos que inciden con alguna recta de \(\Pi_0\text{,}\) es decir,
simplificando tenemos
de otro modo
por lo tanto \(m^2- n \leq 0\text{,}\) es decir, \(n=m^2\) o bien \(n>m^2\)
Si \(n=m^2\) entonces tenemos que
Lo que significa que cada punto del plano proyectivo, esta contenido en una recta del sub-plano.
Si \(n>m^2\text{,}\) entonces existe un punto \(P\text{,}\) el cual no pertenece a ninguna recta del sub-plano, al considerar un punto del sub-plano, existe la recta que pasa por ambos punto, esta recta no puede contener otros punto del sub-plano.
Pero \(P\text{,}\) pasan \(n+1\) rectas, luego tenemos que \(n+1 \geq m^2+m+1\text{,}\) cancelando obtenemos que \(n\geq m^2+m\text{.}\)
Sean \(\mathbb{F}_2\text{,}\) \(\mathbb{F}_4\) y \(\mathbb{F}_8\text{;}\) cuerpos de cardinal 2,4,8 respectivamente.
En el primer caso tenemos que el plano proyectivo \(\Pi_2= \mathbb{P}_{2}(\mathbb{F}_2^{3}) \) tiene orden \(2\) y
En el segundo caso tenemos que el plano proyectivo \(\Pi_4= \mathbb{P}_{2}(\mathbb{F}_4^{3})\) tiene orden \(4\) y
En el último caso tenemos que el plano proyectivo \(\Pi_8=\mathbb{P}_{2}(\mathbb{F}_8^{3})\) tiene orden \(8\) y
Notemos que en este caso \(\Pi_2\) es un subplano de \(\Pi_4\) y se cumple \(4=2^2\text{,}\) y además \(\Pi_2\) es un subplano de \(\Pi_8\) y se cumple \(8\gt 2^2+2=6\text{.}\)