Sección 1.6 Dilataciones del Plano Afín
¶Sean \(\Pi\) un plano afín y \(f \in Aut(\Pi)\text{.}\)
Se dice que \(f\) es dilatación de \(\Pi\) si y sólo si para todos \(l \in \mathcal{L}\) se tiene que
Sean \(\Pi=\mathbb{Z}_{2} \times \mathbb{Z}_{2}\) y \(\begin{array}[t]{rrcl} f:\amp\Pi\amp\longrightarrow \amp\Pi \\ \amp (x,y) \amp \rightsquigarrow \amp(x,y+\overline{1}) \end{array}\)
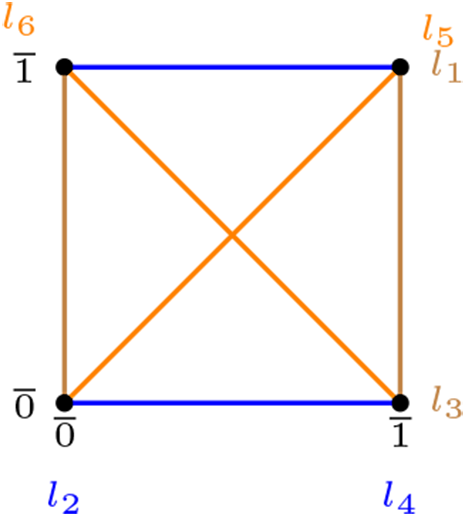
por ello \(f\) es dilatación \(\mathbb{Z}_{2} \times \mathbb{Z}_{2}\)
Ejemplo 1.6.2
Sea \(f: \mathbb{R}^2 \rightarrow \mathbb{R}^2\) tal que \(f(x,y)= (3x,3y)\text{.}\)
Demuestre que \(f\) es una dilatación en el plano afín vectorial
Sea \(l = \lt v \gt + w \in \mathcal{L}\text{,}\) luego tenemos que
Además tenemos que \(\lt v \gt + w \parallel \lt v\gt +3w \text{,}\) por ello \(f\) es una dilatación.
Notación
Sea \(\Pi \) un plano afín.
Teorema 1.6.3
Una dilatación está completamente determinada si se conoce la imagen de dos puntos.
Demostración
Sean \(\Pi\) plano afín, y \(A,B \in \mathcal{P}\) tales que \(f(A)=A', f(B)=B'\text{,}\) con \(f\) dilatación.
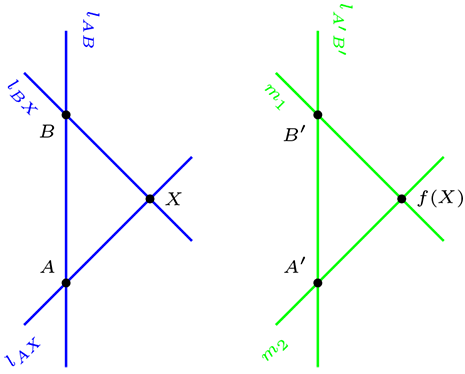
Sea \(X \in \mathcal{P}\) de modo que \(X \neq A \wedge X \neq B\)
-
\(X \ {\not\mathcal{I}} l_{AB}\)
Primero unimos \(X\) con \(B\) a través de la recta \(l_{BX}\text{,}\) por \(B'\) trazamos \(m_1\) tal que \(m_1 \parallel l_{BX}\text{.}\)
Después unimos \(X\) con \(A\) a través de la recta \(l_{AX}\text{,}\) por \(A'\) trazamos \(m_2\) tal que \(m_2 \parallel l_{AX}\text{.}\)
De este modo tenemos que \(\{f(X)\}=m_{1} \cap m_{2}\)
-
\(X \mathcal{I} l_{AB}\)
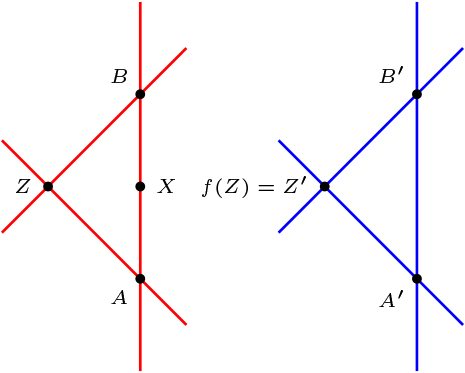
Por el caso anterior, sabemos determinar la imagen de un punto que no es incidente a una recta \(l_{AB}\text{,}\) donde se conoce la imagen de \(A\) y \(B\text{.}\)
Sea \(Z\in \mathcal{P},\ Z \ {\not\mathcal{I}} l_{AB}\text{,}\) como sabemos la imagen de \(A\) y \(B\text{,}\) luego sabemos la imagen de \(Z\text{,}\) es decir, \(f(Z)=Z'\text{.}\) Pero \(X \ {\not\mathcal{I}} \ l_{AZ}\text{,}\) por lo tanto \(f(X)\) se puede determinar.
Observación 1.6.4
Al quedar completamente determinada la dilatación a través de la imagen de dos puntos, entonces al tener dos puntos fijos, se concluye que \(f\) es la identidad, es decir, \(f=Id\text{.}\)
De otro modo \(f \neq Id\text{,}\) entonces \(f\) tiene a lo más un punto fijo.
Definición 1.6.5
Sea \(f\) una dilatación en el plano afín \(\Pi\text{.}\)
Se dice que \(f\) es una Homotecia si y sólo si, \(f\) tiene un punto fijo y este se llama centro de la homotecia o \(f=Id\text{.}\)
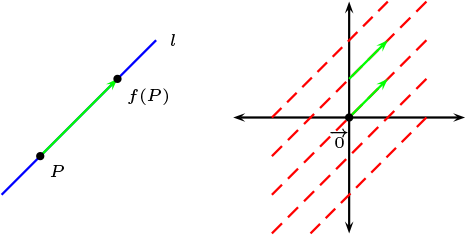
Se dice que \(f\) es una Traslación si y sólo si, \(f\) no tiene puntos fijos o \(f=Id\text{.}\)
Definición 1.6.6
Sean \(l \in \mathcal{L}\) y \(f\) es una dilatación en el plano afín.
Se dice que \(l\) es traza de \(f\) si y sólo si \((\exists P \in \mathcal{P})(P\mathcal{I}l \Rightarrow f(P) \mathcal{I} l)\text{.}\)
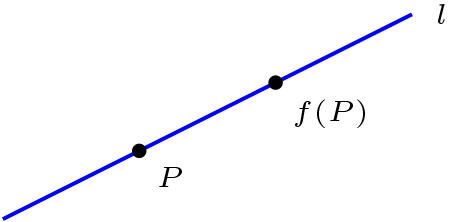
Teorema 1.6.7
Sean \(\Pi\) plano afín y \(f\) dilatación de \(\Pi\text{.}\)
\(f(l)=l\) si y sólo si \(l\) es traza de \(f\text{.}\)
Demostración
Sea \(f\) una dilatación, luego \(f \in \text{Aut}(\Pi)\) y \(f(l)=l\text{.}\) Si \(P\in \mathcal{P}\) tal que \(P \ \mathcal{I} \ l\) luego \(f(P) \ \mathcal{I} \ f(l)\text{,}\) de lo cual \(f(P) \ \mathcal{I} \ l\text{.}\)
Veamos el recíproco.
Si \(l\) es traza de \(f\text{,}\) luego \((\exists P \in \mathcal{P})(P \ \mathcal{I} \ l \Rightarrow f(P) \ \mathcal{I}\ l)\)
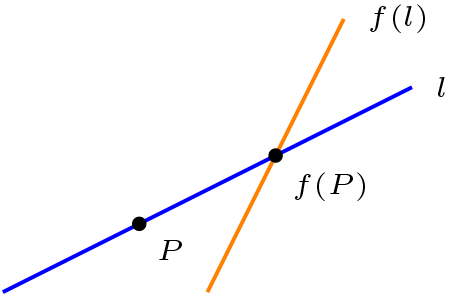
Sea \(Q \ \mathcal{I}\ l\text{,}\) con \(Q\neq P\text{,}\) luego tenemos que \(f(Q) \ \mathcal{I}\ f(l) \text{ y } f(P) \ \mathcal{I} \ f(l) \) es decir \(f(P) \in l \cap f(l)\)
Como \(f\) es dilatación, entonces \(f(l) \parallel l \text{ } \wedge \text{ } l \cap f(l) \neq \varnothing\) en consecuencia \(f(l)=l\text{,}\) lo cual implica que \(l\) es traza de \(f\text{.}\)
Proposición 1.6.8
Sea \(f\) una homotecia distinta de la identidad y \(P\) centro de la homotecia \(f\text{,}\) entonces cada recta que pasa por \(P\) es una traza de \(f\text{.}\)
Demostración
Sea \(Q\in \mathcal{P}\) y \(l_{PQ}\in \mathcal{L}\text{,}\) luego tenemos \(f(l_{PQ}) \parallel l_{PQ}\text{,}\) pero \(P\mathcal{I}l_{PQ} \) y \(P\mathcal{I}f(l_{PQ})\text{,}\) luego las rectas son iguales.
Proposición 1.6.9
Si \(f\) es una traslación distinta de la identidad entonces no tiene puntos fijos y el conjunto de todas las trazas es un haz de paralelas.
Demostración
Sea \(P\in \mathcal{P}\text{,}\) luego la recta \(l_{Pf(P)}\) es una traza de \(f\text{,}\) es decir existen traza de \(f\text{.}\)
Sea \(l\) otra traza de \(f\text{,}\) luego ambas están fijas por \(f\) y si tiene un punto en común este seria un punto fijo lo que es una contradicción.
En el plano afín vectorial:
Toda recta fija es una traza de la dilatación, además
-
La traza de la homotecia, son las rectas que pasan por el punto fijo, dado que la homotecia tiene un punto fijo \(f(P)=P=(a,b)\text{.}\)
Las trazas de la homotecia las podemos definir como:
\begin{equation*} \{m \in \mathbb{K}\ |\ y=m(x-a)+b\} \cup \{x=a\} \end{equation*}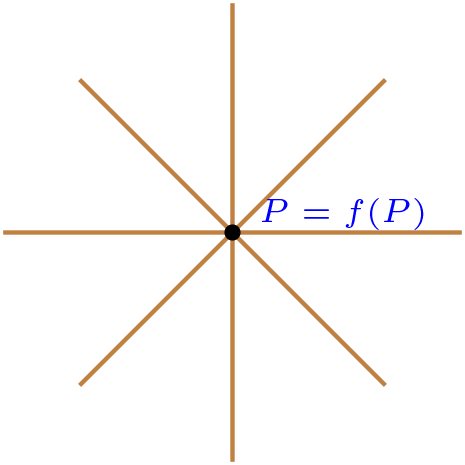
-
Las traslaciones no tienen puntos fijos.
Además dejan fijas todas las rectas que tiene vector director \(\overrightarrow{Pf(P)}\) y por ende el haz de paralelas formada por ellas.
Ejemplo 1.6.10
Consideremos la homotecia en el plano afín vectorial
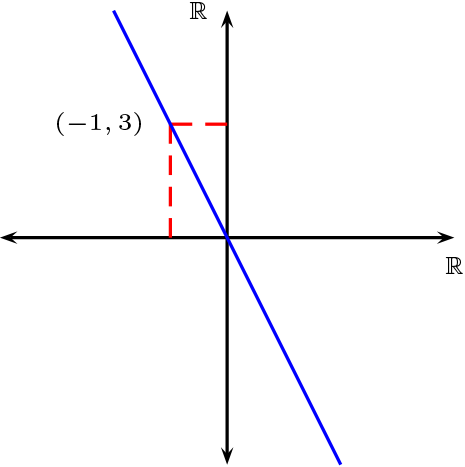
Tiene un punto fijo \((-1,3)\text{,}\) las rectas fijas están dada por \(l_\infty : x=-1\) ya que \(f(l_\infty) =l_\infty \) y \(l_m:\langle (1,m)\rangle+(-1,3)\) que cumple con \(f(l_m) =l_m\text{.}\)
Ejemplo 1.6.11
Consideremos la traslación en el plano afín vectorial
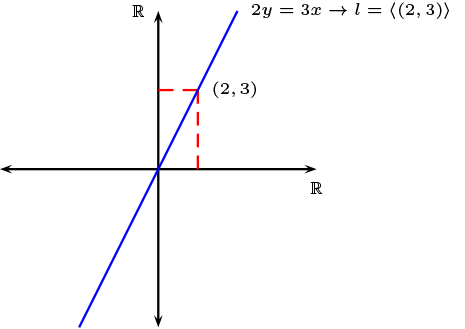
Tiene rectas fijas, pero dada las rectas \(l:\langle (2,3)\rangle+(a,b)\) y \(f(l):\langle (2,3)\rangle+(a,b)\text{,}\) además el haz de recta \([l]\text{,}\) también esta fijo que \(f([l])=[l]\text{.}\)
Teorema 1.6.12
Una traslación esta completamente determinada si se conoce la imagen de un punto.
Demostración
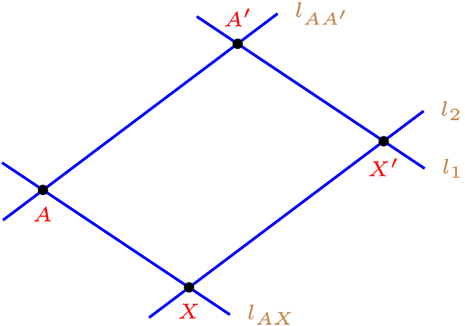
Sea \(A \in \mathcal{P}\) tal que \(f(A)=A'\text{,}\) como \(A,A'\) son distintos existe \(l_{AA'}\) y \(X \in \mathcal{P}\text{,}\) tal que \(X {\not\mathcal{I}} l_{AA'}\text{.}\)
Definimos:
\(l_2\) paralela a \(l_{AA'}\) y \(X \ \mathcal{I} \ l_2\) es una traza de \(f\) luego esta fija por \(f\text{.}\)
\(l_1\) paralela a \(l_{AX}\) y \(A' \ \mathcal{I} \ l_1\text{,}\) note que \(f(l_{AX})= l_1\) es paralela y \(A'\) incide en ella.
Por lo tanto, \(l_1, l_2\) no son paralela, luego \(l_1 \cap l_2 = \{ f(X) \}\text{.}\)
De este modo tenemos que \(f(A)=A'\) y \(f(X)= X'\text{,}\) dos imagen, por propiedad de dilatación, define una única dilatación.
Corolario 1.6.13
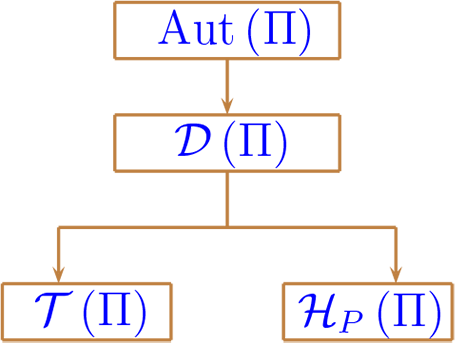
Sea \(\mathcal{T}(\Pi)=\{ f\in \mathcal{D}(\Pi) \ |\ f \text{ traslación } \}\) es un grupo, llamado grupo de las traslaciones de \(\Pi\)
Demostración
Es un subconjunto no vacío y la inversa es una traslación, ahora veamos la compuesta de dos traslaciones es una traslación o una homotecia, si tenemos que es una homotecia tendría un punto fijo despejando obtenemos que dos traslaciones tiene un punto en común luego son iguales y por ende es una traslación.
Corolario 1.6.14
Sea \(\mathcal{H}_P (\Pi)=\{ f\in \mathcal{D}(\Pi) \ |\ f \text{ homotecia tal que } f(P) \}\) es un grupo, llamado grupo de las homotecias de \(\Pi\) que tienen centro en \(P\text{.}\)
Demostración
Es un subconjunto no vacío y la inversa es una homotecia, ya que deja fija un punto, y la compuesta de dos homotecias de centro \(P\text{,}\) el punto \(P\) esta fijo, luego es una homotecia de cento \(P\text{.}\)
Observación 1.6.15
Denotemos \(\mathcal{D}(\Pi)=\{f:\Pi \longrightarrow \Pi \ |\ f \text{ difamación } \}\) en donde se tiene que \((\mathcal{D}(\Pi),\circ)\) es un grupo, llamado grupo de las dilataciones de \(\Pi\text{,}\) además \(\mathcal{D}(\Pi)\leq Aut(\Pi)\) y \(\mathcal{H}_P(\Pi)\leq Aut(\Pi)\text{.}\)