Sección 1.10 Ejemplos Misceláneos
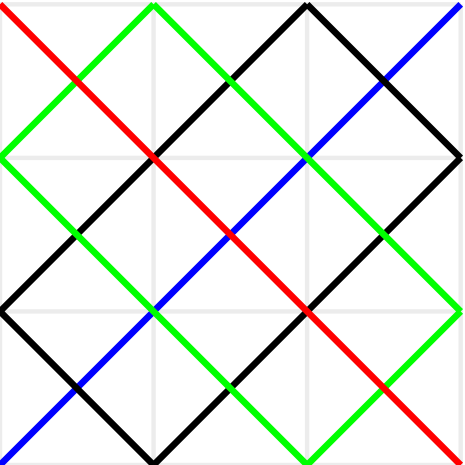
¶Considere \(\mathbb{K}=\{a+b\delta\ |\ a,b \in \mathbb{Z}_2\}=\mathbb{Z}_2(\delta)\text{,}\) es un cuerpo con 4 elementos, donde \(\delta^2=\delta +1\) y \(\Pi\) es el plano afín vectorial, es decir,
\begin{equation*}
\mathcal{P}= \mathbb{K}^2,\qquad\mathbb{L}= \{ \lt w \gt+v\ |\ v,w\in \mathbb{K}^2, w\neq 0\}\ \text{ y }\ I:\text{pertenecía}
\end{equation*}
Graficar los puntos y las rectas en \(\mathbb{K}^2\text{,}\) identificando los haces paralelas.
\(\mathbb{K}=\{0,1, \delta, 1+\delta\}= \mathbb{Z}_2(\delta)\text{,}\) cuerpo con 4 elementos
El número de: Puntos es \(4^2=16\text{,}\) Rectas \(20=16+4\text{,}\) Haces es \(5\) y cada haz contiene 4 rectas.
Ejemplo 1.10.2
Considere la estructura de incidencia dada por los puntos \(\mathcal{P}=\{(x,y)\in \mathbb{R}^2\ | \ y>0 \}\) semiplano superior, la recta \(c_{a,r} =\{(x,y)\in \mathcal{P}\ | \ (x-a)^2+y^2=r^2 \}\) una semicircunferencia con centro eje \(x\text{,}\) el conjunto de las rectas \(\mathcal{L}= \{ c_{a,r}\ | \ a,r\in \mathbb{R}, r>0 \}\) y la incidencia es la pertenecía.
Determine que axiomas de plano afín cumple \(\Pi= (\mathcal{P},\mathcal{L},\mathcal{I} )\text{.}\)
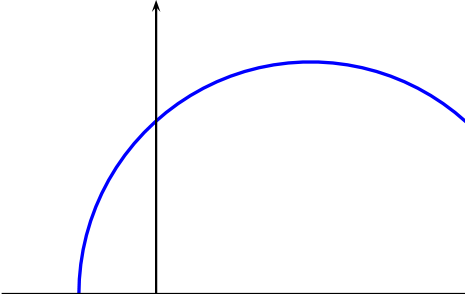
Primer axioma, dado los puntos distintos \((a,b),(c,d)\in \mathcal{P}\) deben pertenecer a una única recta.
\begin{equation*}
(
x-h)^2+ y^2= r^2,
\end{equation*}
reemplazando tenemos \((a-h)^2+ b^2= r^2\text{,}\) \((c-h)^2+ d^2= r^2\text{.}\)
Restando las ecuaciones obtenemos que \(2ah-2ch= d^2+c^2-b^2-a^2\text{,}\) cuando \(a=c\text{,}\) tenemos que \(b\neq d\) y positivos luego la ecuación no tiene solución, no cumple axioma 1.
Segundo axioma, dada la recta. \((x-h)^2+ y^2= r^2\text{,}\) y el punto \((a,b)\) que no pertenece a la recta, entonces la recta
\begin{equation*}
(x-h)^2+ y^2= (a-h)^2+ b^2
\end{equation*}
es una recta paralela que pasa por el punto \((a,b)\text{,}\) no es única.
Tercer axioma, los puntos \((1,1),(1,2), (-1,1)\text{,}\) no son colineales, no existe recta que une los puntos \((1,1),(1,2)\)
Ejemplo 1.10.3
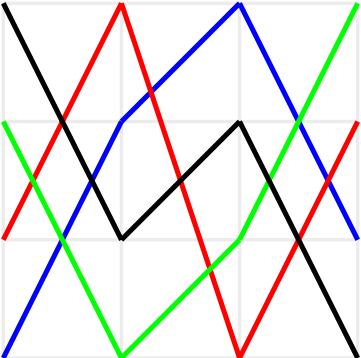
En \(\Pi\) Plano de Moulton, sea los puntos \(A=(-1,9)\text{,}\) \(B=(2,-3)\) y \(C=(-2,5)\text{.}\)
Determinar la ecuación de la recta \(m\text{,}\) tal que \(m\parallel l_{AB}\) y \(C \mathcal{I} m\text{.}\)
La recta \(l_{AB}\) tiene pendiente negativa.
\begin{equation*}
l_{AB}:y= \left\{ \begin{array}{ccc}
ax+b \amp ; \amp x \geq 0 \\ \\
\frac{a}{2}x+b \amp ; \amp x \lt 0
\end{array} \right.
\end{equation*}
luego, reemplazamos \(A\) y \(B\) y se tiene que \(9 =-a/2+b\) y \(-3=2a+b\text{,}\) de lo cual restando se obtiene que \(a= -\frac{24}{5} \text{.}\)
De este modo, la recta \(m\) esta dada por:
\begin{equation*}
m:y= \left\{ \begin{array}{ccc}
-\frac{24}{5}x+c \amp; \amp x \geq 0 \\ \\
-\frac{12}{5}x+c \amp ; \amp x \lt 0
\end{array} \right.
\end{equation*}
Reemplazando el punto \(C\) obtenemos que \(5=\frac{24}{5}+c\text{,}\) de lo cual tenemos que \(c= \frac{1}{5}\text{.}\)
Por lo anterior tenemos
\begin{equation*}
m:y= \left\{ \begin{array}{ccc}
-\frac{24}{5}x+\frac{1}{5}\amp ; \amp x \geq 0 \\ \\
-\frac{12}{5}x+\frac{1}{5} \amp ; \amp x \lt 0
\end{array} \right.
\end{equation*}
Ejemplo 1.10.4
En \(\Pi\) Plano de Moulton, sea \(T(x,y)= (2x,2y-2)\)
Determinar si \(T\) es una colineación en \(\Pi\text{.}\)
Determinar si \(T\) es una dilatación en \(\Pi\text{.}\)
La función \(T\) es biyectiva, ya que \(T(x, y)= (2x,2y-2)\text{,}\) se tiene que \(F(x,y)= ( \frac{1}{2}x,\frac{1}{2}y+1)\) es la inversa
\begin{equation*}
(F\circ T)(x,y) = F( 2x, 2y-2)= (x, \frac{1}{2}(2y-2)+1)=(x,y)
\end{equation*}
\begin{equation*}
(T\circ F)(x,y) = T( \frac{1}{2}x, \frac{1}{2}y+1)= (x, 2(\frac{1}{2}y+1)-2 )=(x,y)
\end{equation*}
Una es la inversa de la otra, luego \(T\) es biyectiva en puntos.
Veamos ahora los cuatro tipo de rectas:
Rectas horizontal.
\begin{align*}
T (\{ (c,y) \ | \ y \in \mathbb{R}\} )\amp=\amp \{ (2c,2y-2) \ | \ y \in \mathbb{R}\} \\
T (\{ (c,y) \ | \ y \in \mathbb{R}\} )\amp=\amp \{ (2c,z) \ | \ z \in \mathbb{R}\}
\end{align*}
es decir, la recta es horizontal preserva incidencia, paralelismo y la imagen es paralela.
\begin{equation*}
T:\ l:x=c \longrightarrow l':x=2c.
\end{equation*}
Rectas vertical
\begin{align*}
T(\{ (x,c) \ | \ x \in \mathbb{R}\})\amp=\amp \{ (2x,2c-2) \ | \ x \in \mathbb{R}\} \\
T(\{ (x,c) \ | \ x \in \mathbb{R}\})\amp=\amp \{ (z,2c-2) \ | \ z \in \mathbb{R}\}
\end{align*}
es decir, la recta es vertical preserva incidencia, paralelismo y la imagen es paralela.
\begin{equation*}
T:\ l:y=c\longrightarrow l':y=2c-2.
\end{equation*}
Rectas pendiente positiva.
\begin{align*}
T(\{ (x,mx+b) \ | \ x \in \mathbb{R}\})\amp=\amp \{ (2x,2mx+2b-2) \ | \ x \in \mathbb{R}\} \\
T(\{ (x,mx+b) \ | \ x \in \mathbb{R}\})\amp=\amp \{ (z,mz+2b-2) \ | \ z \in \mathbb{R}\}
\end{align*}
es decir, la recta de pendiente es positiva e igual pendiente preserva incidencia, paralelismo y la imagen es paralela.
\begin{equation*}
T:\ l:y=mx+b \longrightarrow l':y=mx+2b-2.
\end{equation*}
Rectas pendiente negativa.
\begin{align*}
\amp\ampT(\{ (x,mx+b) \ | \ x \in \mathbb{R}^+ \}\cup \{ (y, my/2+b) \ | \ y\in \mathbb{R}^-\})\\
\amp=\amp \{ (2x,2mx+2b-2) \ | \ x \in \mathbb{R}^+\}\cup \{ (2y, 2my/2+2b-2) \ | \ y\in \mathbb{R}^-\} \\
\amp=\amp \{ (t,mt+2b-2)\ | \ t\in \mathbb{R}^+\}\cup \{ (k, mk/2+2b-2) \ | \ k\in \mathbb{R}^-\}
\end{align*}
de otro modo la recta \(l\) es enviada en \(l'\text{.}\)
\begin{equation*}
T:\ l:y= \left\{ \begin{array}{ccc}
mx+b \amp ; \amp x \geq 0 \\ \\
\frac{m}{2}x+b \amp ; \amp x \lt 0
\end{array} \right.
\longrightarrow
l':y= \left\{ \begin{array}{ccc}
mx+2b-2 \amp ; \amp x \geq 0 \\ \\
\frac{m}{2}x+2b-2 \amp ; \amp x \lt 0
\end{array} \right.
\end{equation*}
Preserva incidencia, paralelismo y la imagen es paralela.
Luego \(T\) es una dilatación.
Ya que, las rectas por su tipo se mantiene, luego preserva incidencia, paralelismo y es paralela a la imagen.
Ejemplo 1.10.5
En el plano afín vectorial \(V =\mathbb{C}^2\) y \(f\) una colineación definida por
\begin{equation*}
f(a+bi, c+di)= (a-bi,c-di).
\end{equation*}
Determinar los puntos y rectas fijas de \(f\text{.}\)
Los Puntos Fijos
\begin{equation*}
(a+bi, c+di)=f(a+bi, c+di)= (a-bi,c-di).
\end{equation*}
Luego tenemos que
\begin{equation*}
\begin{array}{rcl|}
a\amp=\amp a\\
b\amp=\amp-b \\ \hline
\end{array} \qquad
\begin{array}{rcl|}
c\amp=\amp c\\
d\amp=\amp-d \\ \hline
\end{array}
\end{equation*}
Por ello tenemos que \(b=0,\ d=0\text{.}\)
\begin{equation*}
\{(a+bi, c+di) \in \mathbb{C}^2\ | \ b=0,\ d=0 \}= \mathbb{R}^2
\end{equation*}
Las Rectas Fijas.
La rectas oblicuas \(l_{m,w}=\{ (z,mz+w) \ | \ z \in \mathbb{C}\}\)
\begin{align*}
f(\{ (z,mz+w) \ | \ z \in \mathbb{C}\})\amp=\amp \{ (\overline{z},\overline{mz+w}) \ | \ z \in \mathbb{C}\} \\
f(\{ (z,mz+b) \ | \ z \in \mathbb{C}\})\amp=\amp \{ (z,\overline{m}z+\overline{w}) \ | \ z \in \mathbb{C}\} \\
f(l_{m,w})\amp=\ampl_{\overline{m},\overline{w}}
\end{align*}
Las rectas verticales, \(l_w=\{ (w,z) \ | \ z \in \mathbb{C}\}\text{.}\)
\begin{align*}
f(\{ (w,z) \ | \ z \in \mathbb{C}\})\amp=\amp \{ (\overline{w},\overline{z}) \ | \ z \in \mathbb{C}\} \\
f(\{ (w,z) \ | \ z \in \mathbb{C}\})\amp=\amp \{ (\overline{w},z) \ | \ z \in \mathbb{C}\} \\
f(l_w)\amp=\amp l_{\overline{w}}
\end{align*}
luego las rectas fijas, preservan pendiente e intercepto. Y esta son
\begin{equation*}
\{ l_{m,w}, l_w \ | \ m,w \in \mathbb{R}\}
\end{equation*}
Ejemplo 1.10.6
Sean \(f, g\) colineación en plano afín.
Demostrar directamente que \(g \circ f\) es una colineación.
Sean \(f, g\) dos colineación en plano afín.
De lo anterior tenemos que \(f, g:\mathcal{P} \rightarrow \mathcal{P}\) son biyectiva, luego \(g\circ f:\mathcal{P} \rightarrow \mathcal{P}\) es biyectiva, además \(f,g:\mathcal{L} \rightarrow \mathcal{L}\) son biyectiva, por ello \(g\circ f:\mathcal{L} \rightarrow \mathcal{L}\) es biyectiva.
Preserva Incidencia
Sabemos que \(g,f\) preservan incidencia, sean \(P\mathcal{I}l\text{,}\) aplicando la función \(f\) tenemos que \(f(P)\mathcal{I} f(l)\) y ahora aplicando \(g\) tenemos que \(g(f(P)) \mathcal{I} g(f(l))\text{,}\) es decir, \((g\circ f)(P) \mathcal{I} (g\circ f)(l)\text{.}\)
Preserva Paralelismo
Dado \(m, l\) dos rectas paralelas distintas, tenemos \(f(m) \parallel f(l)\text{,}\) aplicando \(g\) se obtiene
\begin{equation*}
g(f(m)) \parallel g(f(l))
\end{equation*}
De este modo tenemos que \(g\circ f\) es una colineación.
Ejemplo 1.10.7
Demostrar que todo plano afín, contiene al menos tres haces de rectas.
Por el tercer axioma existe tres puntos no colineales \(A,B,C\text{,}\) por axioma 1 existen las rectas \(l_{AB}, l_{AC}, l_{BC}\)
Las rectas no pueden ser iguales, ya que significa que los puntos son colineales y además cada una de ella con la otra tiene una intersección.
\begin{equation*}
l_{AB}\cap l_{AC}=\{A\},\ l_{BC}\cap l_{AB}=\{B\},\ l_{AC}\cap l_{BC}=\{C\}
\end{equation*}
Luego no pueden ser paralela dos a dos
De esta manera cada una de las rectas pertenece a un haz distintos de rectas.
Ejemplo 1.10.8
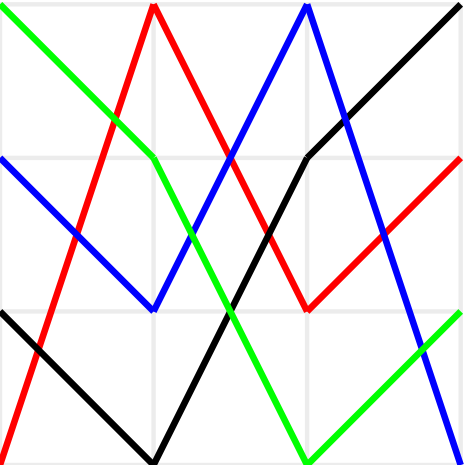
En \(\Pi\) Plano de Moulton Real, sean \(A=(-4,7), B=(3,-3), C=(-2,1)\) y \(D=(1,-7).\)
Determinar \(l_{AB}\cap l_{CD}\text{.}\)
Consideremos las rectas
\begin{equation*}
l_{AB}:y= \left\{ \begin{array}{ccc}
ax+b \amp ; \amp x \geq 0 \\ \\
\frac{a}{2}x+b \amp ; \amp x \lt 0
\end{array}
\right. \qquad
l_{CD}:y= \left\{ \begin{array}{ccc}
cx+d \amp ; \amp x \geq 0 \\ \\
\frac{c}{2}x+d \amp ; \amp x \lt 0
\end{array}
\right.
\end{equation*}
luego, reemplazamos \(A\) y \(B\) se tiene que \(7 =-2a+b\) y \(-3=3a+b\text{,}\)
\begin{equation*}
\begin{array}{rcr|}
-2a+b\amp=\amp7 \\
3a+b \amp=\amp -3\\ \hline
\end{array}
\end{equation*}
de lo cual \(a= -2,\ b=3 \) y en la otra reemplazamos \(C\) y \(D\) se tiene que \(1 =-c+d\) y \(-7=c+d\text{,}\)
\begin{equation*}
\begin{array}{rcr|}
-c+d \amp=\amp1 \\
c+d\amp=\amp -7\\ \hline
\end{array}
\end{equation*}
de lo cual \(c=-4,\ d=-3 \text{.}\) De este modo tenemos
\begin{equation*}
l_{AB}:y=
\left\{ \begin{array}{ccc}
-2x+3 \amp ; \amp x \geq 0 \\ \\
-x+3 \amp ; \amp x \lt 0
\end{array}\right.
\qquad
l_{CD}:y=
\left\{ \begin{array}{ccc}
-4x -3 \amp; \amp x \geq 0 \\ \\
-2x-3 \amp ; \amp x \lt 0
\end{array} \right.
\end{equation*}
Igualando tenemos
\begin{equation*}
\begin{array}{cccc}
\text{Caso }x\geq 0 \amp;\amp \text{Caso } x \lt 0 \\
-2x+3=-4x-3 \amp\amp -x+3=-2x-3 \\
2x=-6 \amp\amp x= -6 \\
x=-3\geq 0 \amp\amp x= -6 \lt 0
\end{array}
\end{equation*}
Luego obtenemos que
\begin{equation*}
l_{AB}\cap l_{CD}=\{(-6,9) \}
\end{equation*}
Ejemplo 1.10.9
En \(\Pi\) Plano de Moulton Real, sean \(A=(-6,6), B=(4,-8)\) y \(C=(-2,5).\)
Determinar la ecuación de la recta \(l\text{,}\) tal que \(l\parallel l_{AB}\) y \(C\mathcal{I} l\text{.}\)
Consideremos las rectas
\begin{equation*}
l_{AB}:y= \left\{ \begin{array}{ccc}
ax+b \amp ; \amp x \geq 0 \\ \\
\frac{a}{2}x+b \amp ; \amp x \lt 0
\end{array}
\right.
\end{equation*}
luego, reemplazamos \(A\) y \(B\) se tiene que \(6 =-3a+b\) y \(-8=4a+b\text{,}\)
\begin{equation*}
\begin{array}{rcr|}
-3a+b\amp=\amp6 \\
4a+b \amp=\amp -8\\ \hline
\end{array}
\end{equation*}
de lo cual \(a= -2,\ b=0 \text{.}\) De este modo tenemos
\begin{equation*}
l_{AB}:y=
\left\{ \begin{array}{ccc}
-2x \amp ; \amp x \geq 0 \\ \\
-x \amp ; \amp x \lt 0
\end{array}\right.
\end{equation*}
La recta paralela
\begin{equation*}
l_{C}:y= \left\{ \begin{array}{ccc}
-2x+d \amp ; \amp x \geq 0 \\ \\
-x+d \amp ; \amp x \lt 0
\end{array}
\right.
\end{equation*}
reemplazamos \(C\) y se tiene que \(5 =2+d\) y \(d=3\text{,}\)
\begin{equation*}
l_{C}:
y=
\left\{ \begin{array}{ccc}
-2x+3 \amp; \amp x \geq 0 \\ \\
-x+3 \amp ; \amp x \lt 0
\end{array} \right.
\end{equation*}
Ejemplo 1.10.10
Considere \(\Pi= ( \mathcal{P}, \mathcal{L}, \mathcal{I}) \text{,}\) plano afín vectorial complejo
\begin{equation*}
\mathcal{P}= \mathbb{C}^2,\qquad\mathcal{L}= \{ \lt w\gt +v\ |\ v,w\in \mathbb{C}^2, w\neq 0\}\ \text{ y }\ I:\text{pertenecía}
\end{equation*}
y \(f_a(z_1,z_2)= (\overline{z_1}+a\overline{z_2},\overline{z_2})\)
Determinar si \(f_a\) es una colineación, con \(a\in \mathbb{C}\text{.}\)
Determinar si \(f_a\) es una dilatación, con \(a\in \mathbb{C}\text{.}\)
Dada la Recta \(l=\{ (bw_1+v_1,bw_2+v_2)\ | \ a\in \mathbb{C} \}= \lt w\gt +v\text{,}\) luego tenemos que
\begin{align*}
f_a(l)\amp=\amp\{ f_a(bw_1+v_1,bw_2+v_2)\ | \ a\in \mathbb{C} \} \\
\amp=\amp\{ (\overline{bw_1}+\overline{v_1}+a\overline{bw_2}+a\overline{v_2}, \overline{bw_2}+\overline{v_2} )\ | \ a\in \mathbb{C} \} \\
\amp=\amp \lt\overline{w_1}+a\overline{w_2},\overline{w_2})\gt +(\overline{v_1}+a\overline{v_2},\overline{v_2} )
\end{align*}
Por ello se concluye que .....
Ejemplo 1.10.11
Considere \(\Pi= ( \mathcal{P}, \mathcal{L}, \mathcal{I}) \text{,}\) plano afín vectorial complejo
\begin{equation*}
\mathcal{P}= \mathbb{C}^2,\qquad\mathcal{L}= \{ \lt w\gt+v\ |\ v,w\in \mathbb{C}^2, w\neq 0\}\ \text{ y }\ I:\text{pertenecía}
\end{equation*}
y \(f(a+bi,c+di)= (a-bi,c-di)\)
Determinar si \(f\) es una colineación
Determinar si \(f\) es una dilatación
Sabemos que \(\overline{z+w}= \overline{z}+\overline{w}\text{;}\) \(\overline{z\cdot w}= \overline{z}\cdot\overline{w}\) y \(\overline{\overline{z}}=z\text{.}\)
Notemos que
\begin{equation*}
f(f(z,w))= f(\overline{z},\overline{w})= (\overline{\overline{z}},\overline{\overline{w}})=(z,w)
\end{equation*}
luego \(f\) es una función biyectiva a nivel de puntos.
En relación a rectas
\begin{align*}
f(\lt(w_1,w_2)\gt+(v_1,v_2)) \amp=\amp \{ f(\alpha(w_1,w_2)+(v_1,v_2)) \ |\ \alpha \in \mathbb{C}\}\\
\amp=\amp \{(\overline{\alpha{w}_1+v_1},\overline{\alpha{w}_2+v_2}) \ |\ \alpha \in \mathbb{C}\} \\
\amp=\amp \{(\overline{\alpha}\overline{w}_1+\overline{v}_1,\overline{\alpha}\overline{w}_2+\overline{v}_2) \ |\ \alpha \in \mathbb{C}\} \\
\amp=\amp \{ \overline{\alpha}(\overline{w}_1,\overline{w}_2)+(\overline{v}_1,\overline{v}_2) \ |\ \alpha \in \mathbb{C}\} \\
\amp=\amp \{ \beta(\overline{w}_1,\overline{w}_2)+(\overline{v}_1,\overline{v}_2) \ |\ \beta \in \mathbb{C}\}\\
\amp=\amp \lt(\overline{w}_1,\overline{w}_2)\gt+(\overline{v}_1,\overline{v}_2)
\end{align*}
envía recta en recta y de la misma manera se tiene que \(f\) es biyectiva a nivel de rectas.
\begin{equation*}
f(f(\lt(w_1,w_2)\gt+(v_1,v_2))) =\lt(w_1,w_2)\gt+(v_1,v_2).
\end{equation*}
La incidencia de recta se cumple por el calculo anterior.
Sea \(l\) y \(m\) dos rectas paralelas luego
\begin{equation*}
l: \lt (w_1,w_2)\gt+(v_1,v_2), \quad m: \lt(w_1,w_2)\gt+(z_1,z_2)
\end{equation*}
luego tenemos que
\begin{equation*}
f(l): \lt(\overline{w}_1,\overline{w}_2)\gt+(\overline{v}_1,\overline{v}_2), \quad
f(m): \lt(\overline{w}_1,\overline{w}_2)\gt+(\overline{z}_1,\overline{z}_2)
\end{equation*}
de lo cual tenemos que \(f(l) \parallel f(m)\)
Por todo lo anterior tenemos que \(f\) es una colineación.
Sea \(l:\lt(1,i) \gt \) tenemos que \(f(l): \lt(1,-i)\gt \) pero \(\{ (1,i), (1, -i) \}\) es linealmente independiente, luego \(f(l)\not \parallel l\text{.}\) Y por ello \(f\) mo es una dilatación.
Ejemplo 1.10.12
Considere el plano afín de Moulton \(\Pi= (\mathcal{P},\mathcal{L},\mathcal{I} )\) y \(h_a(x,y)=(ax,ay)\text{.}\)
Determine si \(h_3\) es una dilatación
Determine si \(h_{-3}\) es una dilatación
Sea \(a\in \mathbb{R}^*\text{,}\) tenemos que \(h_{a}(h_{1/a}(x,y) )= (x,y)\text{,}\) luego tenemos que \(h_a\) es biyectiva de puntos.
Rectas horizontal en horizontal
\begin{align*}
h_{a} (\{ (c,y) \ | \ y \in \mathbb{R}\} )\amp=\amp \{ (ac,ay) \ | \ y \in \mathbb{R}\} \\
h_{a} (\{ (c,y) \ | \ y \in \mathbb{R}\} )\amp=\amp \{ (ac,z) \ | \ z \in \mathbb{R}\}
\end{align*}
Rectas vertical en vertical
\begin{align*}
h_{a}(\{ (x,c) \ | \ x \in \mathbb{R}\}\amp=\amp \{ (ax,ac) \ | \ x \in \mathbb{R}\} \\
h_{a}(\{ (x,c) \ | \ x \in \mathbb{R}\}\amp=\amp \{ (z,ac) \ | \ z \in \mathbb{R}\}
\end{align*}
Rectas pendiente positiva en rectas de pendiente positiva
\begin{align*}
h_{a}(\{ (x,mx+b) \ | \ x \in \mathbb{R}\})\amp=\amp \{ (ax,amx+ab) \ | \ x \in \mathbb{R}\}\\
h_{a}(\{ (x,mx+b) \ | \ x \in \mathbb{R}\})\amp=\amp \{ (z,mz+ab) \ | \ z \in \mathbb{R}\}
\end{align*}
Rectas pendiente negativa en rectas de pendiente negativa
\begin{align*}
\amp\amph_{3}(\{ (x,mx+b), (y, my/2+b) \ | \ x \in \mathbb{R}^+, y\in \mathbb{R}^-\})\\
\amp=\amp \{ (3x,3mx+3b), (3y, 3my/2+3b) \ | \ x \in \mathbb{R}^+, y\in \mathbb{R}^-\} \\
\amp=\amp \{ (x,mx+3b), (y, my/2+3b) \ | \ x \in \mathbb{R}^+, y\in \mathbb{R}^-\}
\end{align*}
Luego \(h_3\) es una colineación.
Ya que, las rectas por su tipo se mantiene luego mantiene incidencia y paralelismo.
Rectas pendiente negativa no es enviada en una rectas
\begin{align*}
\amp\amph_{-3}(\{ (x,mx+b), (y, my/2+b) \ | \ x \in \mathbb{R}^+, y\in \mathbb{R}^-\})\\
\amp=\amp \{ (-3x,-3mx-3b), (y, -3my/2-3b) \ | \ x \in \mathbb{R}^+, y\in \mathbb{R}^-\}\\
\amp=\amp \{ (x,mx-3b), (y, my/2-b) \ | \ x \in \mathbb{R}^-, y\in \mathbb{R}^+\}.
\end{align*}
En particular note que los puntos \(\{ (1,-1),(0,0),(-1,0.5)\}\) son colineales
\begin{equation*}
l:y= \left\{ \begin{array}{ccc}
-x \amp ; \amp x \geq 0 \\ \\
-\frac{1}{2}x \amp ; \amp x \lt 0
\end{array} \right.
\end{equation*}
y tenemos que
\begin{equation*}
h_{-3}\{ (1,-1),(0,0),(-1,0.5)\}= \{ (-3,3),(0,0),(3,-1.5)\}
\end{equation*}
Pero los puntos no son colineales, ya que la recta que une los dos primeros punto
\begin{equation*}
m:y= \left\{ \begin{array}{ccc}
-2x \amp ; \amp x \geq 0 \\ \\
-x \amp ; \amp x \lt 0
\end{array} \right.
\end{equation*}
pero el tercero no pertenece a la recta.
Ejemplo 1.10.13
En el plano de Moulton, Sea \(A=(-3,5), B=(4,-2), C=(1,1)\) y \(D=(0,2).\) Calcular \(l_{AB}\cap l_{CD}\)
Sean \(A=(-3,5)\) y \(B=(4,-2)\)
\begin{equation*}
l_1:y= \left\{ \begin{array}{ccc}
\frac{-14}{11}x+\frac{34}{11} \amp ; \amp x \geq 0 \\ \\
\frac{-7}{11}x+\frac{34}{11} \amp ; \amp x \lt 0
\end{array} \right.
\end{equation*}
Sean \(C=(1,1)\) y \(D=(0,2).\)
\begin{equation*}
l_2:y= \left\{ \begin{array}{ccc}
-x+2 \amp ; \amp x \geq 0 \\ \\
\frac{-1}{2}x+2 \amp ; \amp x \lt 0
\end{array} \right.
\end{equation*}
Para \(x \lt 0\text{,}\) tenemos
\begin{align*}
\frac{-7}{11}x+\frac{34}{11} \amp=\amp \frac{-1}{2}x+2 \\
\frac{-7}{11}x +\frac{1}{2}x \amp=\amp 2-\frac{34}{11} \\
\frac{-3}{22}x \amp=\amp -\frac{12}{11} \\
x\amp=\amp 8\lt 0
\end{align*}
Para \(x\geq 0\text{,}\) tenemos
\begin{align*}
\frac{-14}{11}x+\frac{34}{11} \amp=\amp -x+2 \\
\frac{-14}{11}x +x \amp=\amp 2-\frac{34}{11} \\
\frac{-3}{11}x \amp=\amp -\frac{12}{11} \\
x\amp=\amp 4\geq 0
\end{align*}
Luego tenemos
\begin{equation*}
l_1\cap l_2 =\{(4,-2)\}.
\end{equation*}
Ejemplo 1.10.14
Demostrar directamente que si \(f\) es una colineación en plano afín entonces \(f^{-1}\) también es una colineación.
Sea \(\Pi\) un plano afín, y \(f\) una colineación de \(\Pi\text{.}\)
De lo anterior tenemos que \(f:\mathcal{P} \rightarrow \mathcal{P}\) es biyectiva, luego \(f^{-1}:\mathcal{P} \rightarrow \mathcal{P}\) es biyectiva, además \(f:\mathcal{L} \rightarrow \mathcal{L}\) es biyectiva, por ello \(f^{-1}:\mathcal{L} \rightarrow \mathcal{L}\) es biyectiva.
Sabemos que \(f\) mantiene incidencia, sean \(P\mathcal{I}l\text{,}\) aplicando la función inversa tenemos \(f^{-1}(P)\) es un punto y \(f^{-1}(l)\) es una recta, luego existe \(m\) recta tal que \(f^{-1}(P)\mathcal{I} m\) y \(f^{-1}(l) \parallel m\text{,}\) aplicando \(f\) tenemos que \(P \mathcal{I} f(m)\) y \(l \parallel f(m)\text{.}\) Por lo tanto \(f(m)= l\text{,}\) es decir \(m= f^{-1}(l)\text{,}\) de lo cual se tiene que
\begin{equation*}
f^{-1}(P)\mathcal{I} f^{-1}(l).
\end{equation*}
Dado \(m, l\) dos rectas paralelas distintas, tenemos \(f^{-1}(m)\) y \(f^{-1}(l)\) son dos rectas distintas.
Supongamos que \(Q \mathcal{I} f^{-1}(m)\) y \(Q \mathcal{I}f^{-1}(l)\text{,}\) aplicando \(f\) tenemos
\begin{equation*}
f(Q) \mathcal{I} m \ \wedge f(Q) \mathcal{I} l
\end{equation*}
lo cual es una contradicción, ya que son paralelas y distintas, luego \(f^{-1}(m)\) y \(f^{-1}(l)\) no tiene punto en común, por lo tanto son paralelas.
Ejemplo 1.10.15
Sea \(f\) una dilatación en el plano vectorial real tal que \(f(0,0)=(2,1)\text{,}\) \(f(0,4)=(2,4)\text{.}\)
Determine \(f(x,y)\)
Ya que \(f\) es una dilatación se tiene que \(f(X)= \alpha X + Y\text{.}\)
Luego obtenemos el siguiente sistema
\begin{equation*}
\begin{array}{rcl|}
(2,1)\amp=\amp \alpha (0,0)+ Y \\
(2,4)\amp=\amp \alpha (0,4)+Y \\ \hline
\end{array}
\end{equation*}
De la primera ecuación tenemos que \(Y= (2,1)\text{,}\) reemplazando en la segunda \((0,3) = \alpha (0,4) \) por ende \(\alpha = \frac{3}{4}\text{,}\) de este modo
\begin{equation*}
f(x,y)= \frac{3}{4}(x,y)+ (2,1)=\left( \frac{3}{4}x+2, \frac{3}{4}y + 1\right).
\end{equation*}
Ejemplo 1.10.16
Sean \(\Pi=\mathbb{F}_{11}\times \mathbb{F}_{11}\) plano afín vectorial y \(f \in D(\Pi)\text{,}\) tal que \(f(6,9)=(3,3)\) y \(f(10,1)=(4,1)\)
Determine el cardinalidad del conjunto de trazas de \(f\)
Ya que \(f\) es una dilatación se tiene que \(f(X)= \alpha X + Y\text{.}\)
Luego obtenemos el siguiente sistema
\begin{equation*}
\begin{array}{rcl|}
(3,3)\amp=\amp \alpha (6,9)+ Y \\
(4,1)\amp=\amp \alpha (10,1)+Y \\ \hline
\end{array}
\end{equation*}
Restando las ecuaciones se obtiene \((1,-2) = \alpha (4,-8) \) por ende \(\alpha = 3\text{.}\) reemplazando en la primera ecuación tenemos que \((3,3)= 3(6,9)+ Y\text{,}\) de lo cual \(Y=(-4,-2)\text{,}\) de este modo
\begin{equation*}
f(x,y)= 3(x,y)+ (7,9)=\left( 3x+7, 3y + 9\right).
\end{equation*}
El punto fijo es \((2,1)\) y razón \(3\text{.}\) Por ello es una homotecia.
El conjunto de recta fija esta dada por:
\begin{equation*}
\{ l+ (2,1)\ |\ l \text{ es una recta vectorial }\}
\end{equation*}
y el cardinal de todas las rectas fija es \(12\text{.}\) (cantidad de pendiente +1).
Ejemplo 1.10.17
Sea \(T\) una traslación en el plano afín vectorial \(V=\mathbb{F}_{5}\times \mathbb{F}_{5}\) tal que \(T(3,5)=(-1,7)\) y \(\sigma\) una homotecia de centro \((8,7)\) y razón \(2\)
Determine \((T \circ \sigma)(x,y)\)
Calcular \((T^{-1} \circ \sigma^{-1} \circ T)(x,y)\)
Como \(T\) es una traslación y \(T(3,5)= (-1,7)\text{,}\) tenemos que
\begin{equation*}
T(x,y)=(x+1, y+2).
\end{equation*}
Por otro lado \(\sigma\) es una homotecia de razón \(2\) y centro \((3,2)\text{,}\) luego
\begin{equation*}
\sigma(x,y) = 2(x,y)+ 4(3,2)= (2x+2, 2y+3).
\end{equation*}
Evaluando obtenemos
\begin{equation*}
(T \circ \sigma)(x,y)= T( 2x+2, 2y+3)= (2x+3,2y)
\end{equation*}
Las inversas de \(T\) y \(\sigma\) son:
\begin{equation*}
T^{-1}(x,y)= (x-1,y-2)= (x+4,y+3), \quad \sigma^{-1}(x,y)=( 3x+4, 3y+1)
\end{equation*}
\begin{align*}
\end{align*}
de este modo tenemos
\begin{equation*}
(T^{-1} \circ \sigma^{-1} \circ T)(x,y)= (3x+1,3y+1)
\end{equation*}
Ejemplo 1.10.18
En un plano afín.
Demostrar que una traslación esta completamente determinada si se conoce la imagen de un punto.
Sea \(A \in \mathcal{P}\) tal que \(f(A)=A'\text{,}\) como \(A,A'\) son distintos existe \(l_{AA'}\) y \(X \in \mathcal{P}\text{,}\) tal que \(X {\not\mathcal{I}} l_{AA'}\text{.}\)
Definimos:
\(l_2\) paralela a \(l_{AA'}\) y \(X \ \mathcal{I} \ l_2\) es una traza de \(f\) luego esta fija por \(f\text{.}\)
\(l_1\) paralela a \(l_{AX}\) y \(A' \ \mathcal{I} \ l_1\text{,}\) note que \(f(l_{AX})= l_1\) es paralela y \(A'\) incide en ella.
Por lo tanto, \(l_1, l_2\) no son paralela, luego \(l_1 \cap l_2 = \{ f(X) \}\text{.}\)
De este modo tenemos que \(f(A)=A'\) y \(f(X)= X'\text{,}\) dos imagen, por propiedad de dilatación, define una única dilatación.
Ejemplo 1.10.19
En el plano afín vectorial real, dados cuatro puntos \(A,B,C,D\in \mathbb{R}^2\) distintos, tal que \(l_{AB} \parallel l_{CD}\)
Demostrar que existe una dilatación \(f\) tal que \(f(A)=C\) y \(f(B)=D\)
La existencia de la dilatación \(f(X)= \alpha X + Y\text{,}\) depende que el siguiente sistema tenga solución
\begin{equation*}
\begin{array}{rcl|}
C\amp=\amp \alpha A+Y \\
D\amp=\amp \alpha B+Y \\ \hline
\end{array}
\end{equation*}
Restando las ecuaciones se obtiene \(C-D = \alpha (A-B)\text{,}\) lo cual tiene solución, ya que \(l_{AB} \parallel l_{CD}\text{,}\) y por ello los vectores directores son linealmente dependiente.
Sea \(\beta \) la solución de la ecuación vectorial, luego \(Y= C-\beta A= D- \beta B\text{.}\)
Por lo tanto existe la dilatación y esta dada por:
\begin{equation*}
f(X)= \beta (X-A)+ C
\end{equation*}