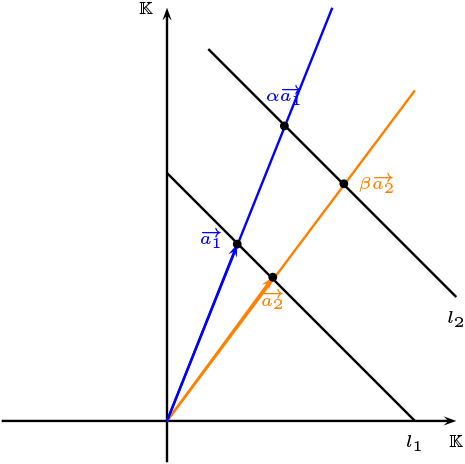
Sea \(\mu\in Aut(\Pi)\text{,}\) por propiedad \ref{prop1.64} se tiene que existen una traslación, una transformación lineal biyectiva en el plano y una base \(\{\overrightarrow{a_1}, \overrightarrow{a_2}\}\) de \(\mathbb{K}^2\text{,}\) tal que si \(\delta =f^{-1} \circ t \circ \mu\text{,}\) \(\delta ( \overrightarrow{0})=\overrightarrow{0},\ \delta(\overrightarrow{a_1})=\overrightarrow{a_1},\ \delta (\overrightarrow{a_2})=\overrightarrow{a_2}\text{.}\)
Por la propiedad \ref{prop1.65} tenemos que
\begin{equation*}
\delta(\alpha\overrightarrow{a_1}+\beta\overrightarrow{a_2})= \delta(\alpha\overrightarrow{a_1})+
\delta(\beta\overrightarrow{a_2}) ,\
\delta(\alpha\overrightarrow{a_1})= \eta(\alpha)\overrightarrow{a_1},\
\delta(\beta\overrightarrow{a_2})>= \eta( \alpha) \overrightarrow{a_2}
\end{equation*}
Definamos
\begin{equation*}
\eta: \mathbb{K} \rightarrow\mathbb{K} \text{ tal que } \eta(\alpha)\text{ cumple con } \delta(\alpha \overrightarrow{a_1})= \eta(\alpha) \overrightarrow{a_1}
\end{equation*}
note que \(\eta(1)=1\) y \(\eta (0)=0\text{.}\)
Es inyectiva, ya que \(\eta (\alpha) = \eta (\beta)\) entonces,
\begin{align*}
\eta (\alpha) \amp=\amp \eta (\beta) \\
\eta (\alpha)\overrightarrow{a_1} \amp=\amp \eta (\beta)\overrightarrow{a_1} \\
\delta (\alpha\overrightarrow{a_1}) \amp=\amp \delta (\beta\overrightarrow{a_1}) \\
\alpha\overrightarrow{a_1} \amp=\amp \beta\overrightarrow{a_1} \\
\alpha \amp=\amp \beta
\end{align*}
Epiyectiva, sabemos la restricción de \(\delta : \lt\overrightarrow{a_1}\gt\rightarrow \lt \overrightarrow{a_1} \gt\) es una biyección luego dado \(\beta \in \mathbb{K}\text{,}\) tenemos que \(\beta\overrightarrow{a_1} \in \lt\overrightarrow{a_1}\gt\text{,}\) luego existe \(\alpha \in \mathbb{K}\text{,}\) tal que \(\delta(\alpha\overrightarrow{a_1})=\beta\overrightarrow{a_1}\)
Para el producto, sea
\begin{equation*}
l_5:\lt\alpha\overrightarrow{a_1}+\overrightarrow{a_2}\gt-\beta\overrightarrow{a_2}
\end{equation*}
luego tenemos
\begin{equation*}
\delta(l_5) = \lt\eta(\alpha)\overrightarrow{a_1}+\overrightarrow{a_2}\gt+\eta(-\beta)\overrightarrow{a_2}
\end{equation*}
pero \(\beta\alpha\overrightarrow{a_1}\in l_5\) de lo cual tenemos \(\delta( \beta\alpha\overrightarrow{a_1}) \in \delta(l_5)\) de este modo tenemos que
\begin{equation*}
\eta(\beta\alpha) \overrightarrow{a_1}\in \lt\eta(\alpha)\overrightarrow{a_1}+\overrightarrow{a_2}\gt+\eta(-\beta)\overrightarrow{a_2}
\end{equation*}
luego tenemos
\begin{equation*}
\eta(\beta\alpha) \overrightarrow{a_1}= -\eta(\alpha)\eta(-\beta)\overrightarrow{a_1}
\end{equation*}
por ello tenemos
\begin{equation*}
\eta(\beta\alpha) = -\eta(\alpha)\eta(-\beta)
\end{equation*}
Para \(\alpha=1=\beta\) tenemos que \(\eta (-1)=-1\text{,}\) además
\begin{equation*}
\eta(-\beta) = \eta(-\beta\cdot 1)= -\eta(1)\eta(\beta)=-\eta(\beta)
\end{equation*}
de lo cual
\begin{equation*}
\eta(\beta\alpha) = -\eta(\alpha)\eta(-\beta)= \eta(\alpha)\eta(\beta).
\end{equation*}
Finalmente para la aditiva \(\eta (\alpha + \beta)=\eta (\alpha )+\eta (\beta) \text{.}\)
\begin{equation*}
l_6:\lt\alpha\overrightarrow{a_1}-\overrightarrow{a_2}\gt+\beta\overrightarrow{a_1}+ \overrightarrow{a_2}
\end{equation*}
luego tenemos
\begin{equation*}
\delta(l_6) = \lt\eta(\alpha)\overrightarrow{a_1}-\overrightarrow{a_2}\gt \eta(\beta)\overrightarrow{a_1}+\overrightarrow{a_2}
\end{equation*}
pero \((\alpha+\beta)\overrightarrow{a_1}\in l_6\) de lo cual tenemos \(\delta( (\alpha+\beta)\overrightarrow{a_1}) \in \delta(l_6)\)
de este modo tenemos que
\begin{equation*}
\eta(\alpha+\beta) \overrightarrow{a_1}\in \lt\eta(\alpha)\overrightarrow{a_1}-\overrightarrow{a_2}\gt+\eta(\beta)\overrightarrow{a_1}+ \overrightarrow{a_2}
\end{equation*}
luego tenemos
\begin{equation*}
\eta(\alpha+\beta) \overrightarrow{a_1}= (\eta(\alpha)+\eta(\beta))\overrightarrow{a_1}
\end{equation*}
por ello tenemos
\begin{equation*}
\eta(\alpha+ \beta) =\eta(\beta)+ \eta(\alpha)
\end{equation*}
De lo cual tenemos que \(\delta \) es semi lineal, y por ello \(f\circ \delta\) es semilineal
\begin{equation*}
\mu = t_{\mu(0)} \circ (f\circ \delta)
\end{equation*}