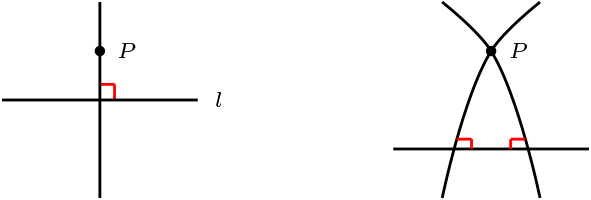Geo-Afín Introducción

Sección 3.1 Introducción

Para enunciar los axiomas del plano métrico, consideremos $\Pi=(\mathcal{P},\ \mathcal{L}, \ \mathcal{I}, \ \perp)$ donde $\mathcal{P}$ es el conjunto de puntos, $\mathcal{L}$ es el conjunto de rectas, $\mathcal{I}$ una relación de incidencia entre puntos y rectas y $\perp$ una relación ortogonalidad entre rectas.

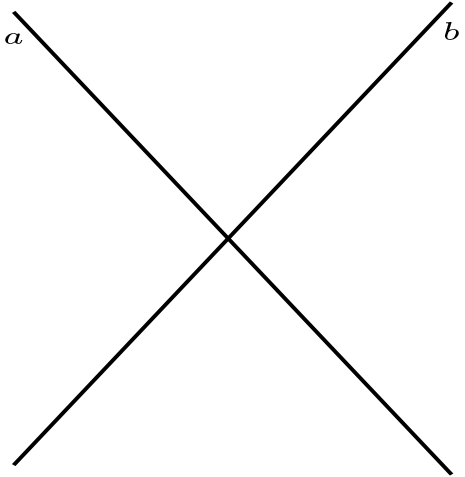
$a \perp b$

$a \not \perp b$

Ahora veamos los tres tipos de axiomas (afines, perpendicular y colineación).

Subsección 3.1.1 Axiomas Afines

Si $A,B \in \mathcal{P}, A \neq B$ entonces $(\exists ! l \in \mathcal{L})( A \mathcal{I} l \wedge B \mathcal{I} l)$
Cada recta contiene al menos tres puntos.
Existe un triángulo (tres puntos no colineales).

Subsección 3.1.2 Axiomas de Ortogonalidad

Sean $l,m \in \mathcal{L}$ tal que, si $l \perp m$ entonces $m \perp l$ ( $\perp$ es simétrico)
Sean $P \in \mathcal{P}, l \in \mathcal{L}$ entonces existe $m \in \mathcal{L}$ tal que $P \ \mathcal{I} \ m \text{ y } m \perp l$

Además si $P \mathcal{I} l \text{,}$ entonces $m$ es única.
Si $l \perp m, \text{ entonces } l \cap m \neq \varnothing .$

Definición 3.1.1

Sean $\Pi=(\mathcal{P},\mathcal{L},\mathcal{I},\perp)$ plano que cumple los axiomas afines y de ortogonalidad y $f$ una función biyectiva, se dice que $f$ es una colineación del plano $\Pi$ si y sólo si

$f:\mathcal{L}\longrightarrow \mathcal{L}$ y $f:\mathcal{P} \longrightarrow \mathcal{P}$ son biyectiva.
Preserva incidencia:

Para todo $P,l$ se tiene que si $P\mathcal{I}l\text{,}$ entonces $f(P)\mathcal{I}f(l)\text{.}$
Preserva Ortogonalidad.

Para todo $l,m$ se tiene que si $l \perp m\text{,}$ entonces $f(l) \perp f(m)\text{.}$

Notación

$\begin{equation*} \text{Aut}(\Pi)=\{ f: \Pi \rightarrow \Pi \ | \ f \text{ es colineación}\} \end{equation*}$

Subsección 3.1.3 Simetrías en el plano.

Definición 3.1.2

Sea $R \in \text{Aut}(\Pi)\text{,}$ se dice que $R$ es una simetría de eje $l$ si y sólo si

$R \neq \text{Id}.$
$R$ tiene orden dos.
$R$ fija a todos los puntos de una recta $l$ (eje de simetría).

Notación

$R_l$ es la simetría de eje $l\text{.}$

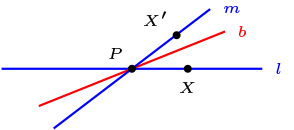
Visualización de una simetría: Sean $P \in \mathcal{P}$ y $a, b \in \mathcal{L}$

Si $P \mathcal{I} a, \text{ entonces } R_{a}(P)=P$
Si $P \not\mathcal{I} a\text{,}$ entonces existe $b \perp a\text{,}$ tal que $P \mathcal{I} b\text{,}$ pero $\{Q\} = a\cap b\text{,}$ luego $b$ es única recta tal que $Q\mathcal{I}b\text{.}$

Pero $R_a(Q)=Q\text{,}$ $R_a(P) \mathcal{I}R_a(b)\text{,}$ $Q \mathcal{I}R_a(b)\text{,}$ y como $R_a(a) \perp R_a(b) \text{,}$ por ello $R_{a}(b)=b\text{,}$ de lo cual tenemos que $R_{a}(P)\mathcal{I}b\text{.}$

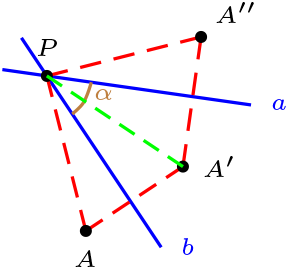
Rotaciones:

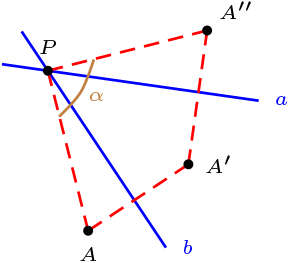
Sea $\sigma \in \text{Aut}(\Pi)\text{,}$ se dice que $\sigma$ es una rotación si y sólo si existen $R_{a}, \ R_{b} \in \text{Aut}(\Pi)\text{,}$ tal que $a \cap b = \{ P \}$ y $\sigma = R_{a} \circ R_{b}\text{.}$

$P$ se denomina centro de rotación.
El ángulo de rotación viene dado por $\alpha=\sphericalangle APA''$ donde $\sigma(A)=A''

En plano real, el ángulo de una rotación siempre es doble del ángulo entre las rectas.

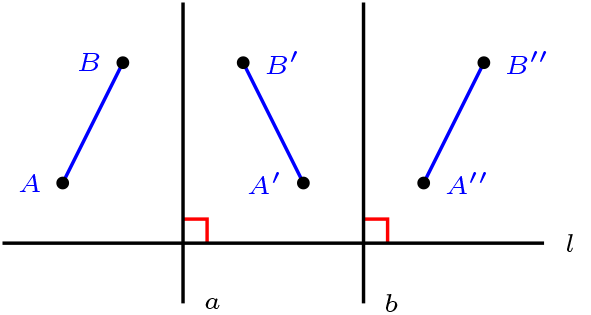
Traslaciones:

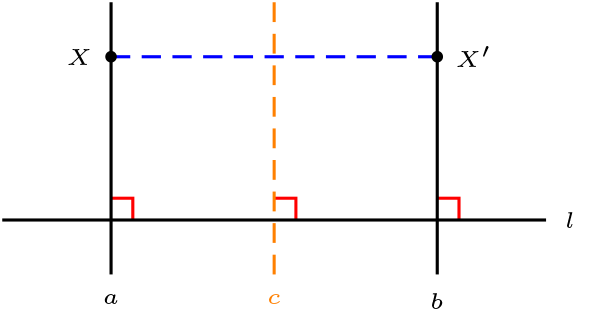
Sea $t \in \text{Aut}(\Pi)\text{.}$ Diremos que $t$ es traslación a lo largo de $l$ si y sólo si existe $a,b \in \mathcal{L}$ tales que $t=R_{a} \circ R_{b}, a \cap b = \varnothing$ y $a \perp l \wedge b \perp l$ ( $R_{a},R_{b}$ simetría).

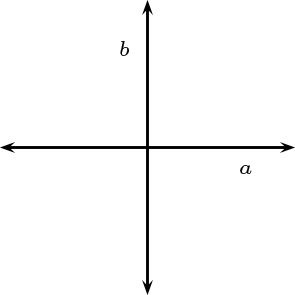
Simetría Puntual

Sea $H_P \in \text{Aut}(\Pi)\text{.}$ Diremos que $H_P$ es una simetría Puntual si y sólo si existen $a,b \in \mathcal{L}$ tales que $H_{P}=R_{a} \circ R_{b}\text{,}$ $a \cap b= \{P\}$ y $a \perp b$

Subsección 3.1.4 Axiomas de Colineaciones

Simetrías
1. Todas recta esta asociada a una única simetría.
  
  $\begin{equation*} \begin{array}{ccc} \mathcal{L} \amp \rightarrow \amp \text{Aut}(\Pi) \\ a \amp \rightarrow \amp R_{a} \end{array} \end{equation*}$
2. El grupo de las colineaciones esta generado por el conjunto de las simetrías del plano afín.
Rotación: Sea $\sigma$ una rotación tal que $\sigma(P)=P$ y $\sigma (l)=m\text{,}$ entonces existe $b \in \mathcal{L}$ tal que $P \ \mathcal{I} \ b$ y $(\forall X \mathcal{I}l)(R_{b}(X)=\sigma(X))$

$\begin{equation*} R_{b}|_{l} = \sigma |_{l} \end{equation*}$
Traslaciones: Sea $t$ traslación a lo largo de la recta $l$ del plano $\Pi\text{.}$

Sean $a,b\in \mathcal{L}$ tales que $a\perp l\wedge b\perp l$ y $t(a)=b\text{,}$ entonces existe $c \in \mathcal{L}$ tal que $c \perp l$ y $(\forall X \mathcal{I}a)(R_{c}(X)=t(X))\text{.}$

donde $c$ se visualiza como la paralela media entre $a$ y $b$