Observación 3.5.1
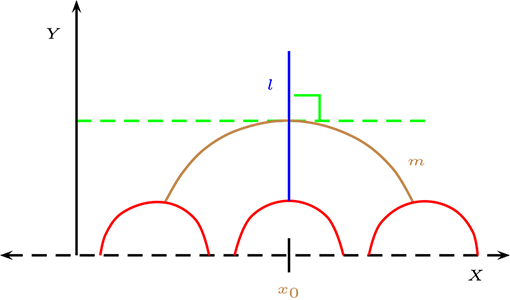
En el caso Euclidiano, solo se tiene que \(m \parallel l\text{.}\)
En esta seccion estudiaremos los planos métricos, que no cumple en quinto axioma de Euclides, es decir, que pasa varias paralelas en un punto dado. Y construiremos modelos de estos planos Hiperbólicos
Un plano hiperbólico \(\Pi=(\mathcal{L},\ \mathcal{P},\ \mathcal{I}, \ \perp)\) es un plano métrico \(\Pi\) que satisface el axioma hiperbólico, es decir,
Los axiomas afines
Los axiomas de ortogonalidad
Los axiomas de colinealidad
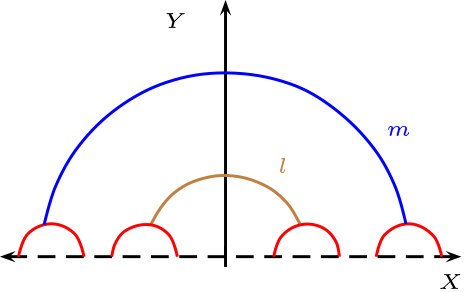
Axioma hiperbólico: Si \(P\in \mathcal{P}\) y \(l \in \mathcal{L}\) tal que \(P \not\mathcal{I} l\) entonces por \(P\) pasan infinitas paralelas a la recta \(l\text{.}\)

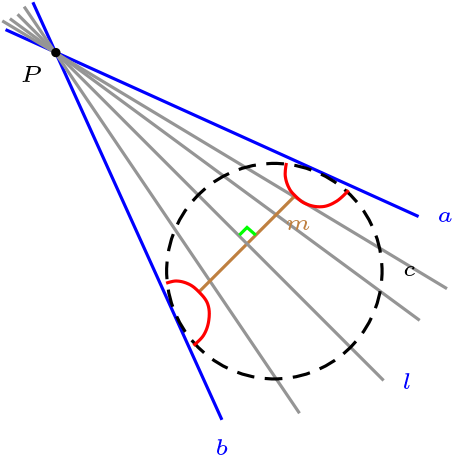
Construyamos el modelo de Klein de un Plano Hiperbólico.
El conjunto de punto del plano, corresponde al interior del circulo unitario, es decir,
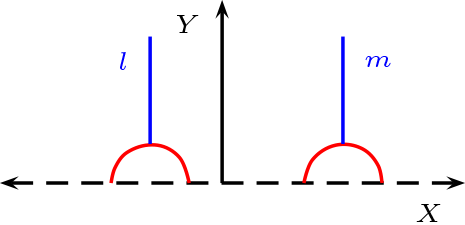
Las rectas del plano, corresponde a las cuerda en el circulo unitario, de otro modo son las recta del plano cartesiano intersecta con el circulo, cuando ella es no vacías, \(l,m \in \mathcal{L}\)
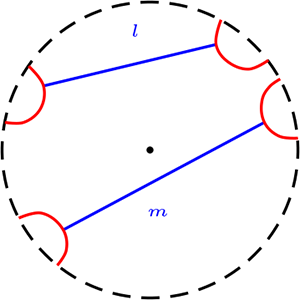
La incidencia corresponde a la pertenecía.
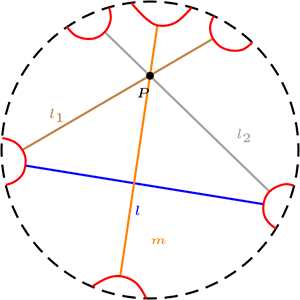
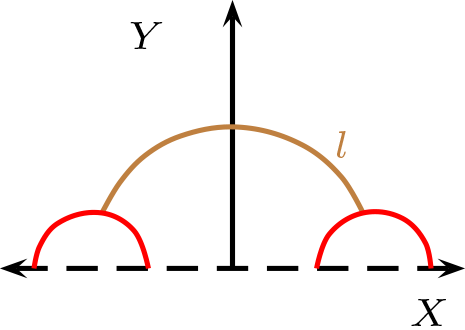
Relación de Paralelismo Dos rectas son paralelas, si no tiene puntos en común.
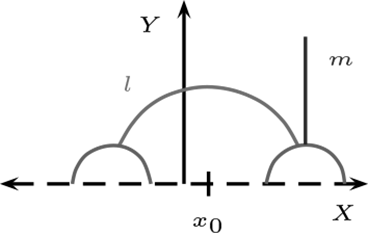
En la figura, las rectas paralelas a \(l\) que pase por \(P\text{,}\) son cualquier recta que pase por \(P\) y se encuentre situada entre las rectas \(l_1\) y \(l_2\text{.}\)
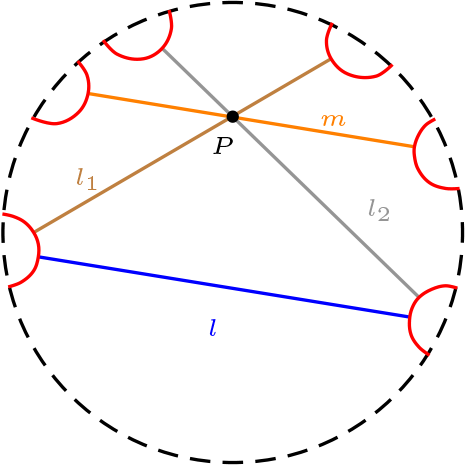
En el caso Euclidiano, solo se tiene que \(m \parallel l\text{.}\)
Relación de Ortogonalidad
Dos rectas \(l,m\in \mathcal{L}\) son ortogonales, si cumple una de las siguientes condiciones
Si \(l\) o \(m\) es un diámetro es la ortogonalidad Euclidiana:
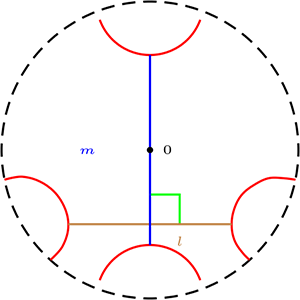
Si ninguna de las cuerdas es un diámetro, trazamos las tangente \(a,b\) a la circunferencia, en los puntos de intersección de la prolongación de \(m\) con la circunferencia, y prolongamos la recta \(l\text{,}\) si la prolongación pasa por el punto de intersección de las tangente, decimos que las recta \(m\) es ortogonal a la recta \(l\text{.}\)
De otro modo, si \(l\perp m\text{,}\) entonces existen tangentes a la circunferencia en los puntos de intersección con las cuerdas, de modo que las extensiones de ambas pasan por los puntos de intersección de las tangentes.
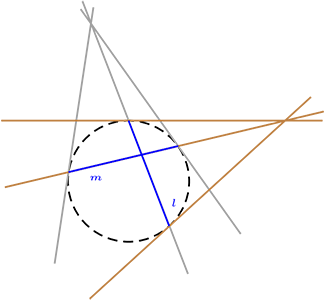
Observación: La ortogonalidad hiperbólica, no respecta paralelismo.
Construyamos el modelo de Poincare, de un plano Hiperbólico.
El conjunto de puntos del plano, son los puntos del semiplano superior del plano cartesiano, es decir,
El conjunto de las rectas, esta formado por dos tipos:
Semirecta Paralelas al eje \(Y\text{;}\) \(l:x=x_{0}\)
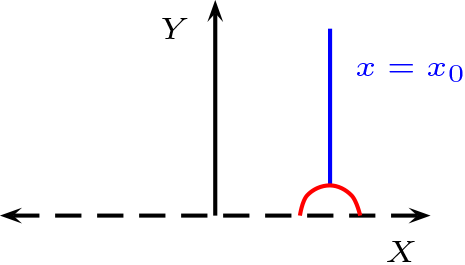
Semicircunferencias \(l:(x-x_{0})^2+y^2=r^2\)

Por dos puntos pasa un única recta. Sean \((x_0,y_0),(x_1,y_1) \in \mathcal{P}\text{.}\)
Si \(x_0=x_1\text{,}\) las recta es \(l:x=x_0\)

Si \(x_0\neq x_1\) entonces, sea \(Q\) el punto medio del segmento que une los puntos \(A(x_0,y_0)\text{,}\) \(B(x_1,y_1)\text{,}\) tracemos la perpendicular, al segmento en \(Q\) y la intersección con el eje \(X\) es el centro de la semicircunferencia y el radio la distancia a uno de los puntos
Sean \(A=(1,2)\) y \(B=(3,5)\) en el plano de Poincare.
Determinar la ecuación de la recta que une los puntos
El punto medio es \(M=(2,\frac{7}{2})\text{,}\) la pendiente de la recta es
Luego la ecuación de la recta tangente esta dada por
Para \(y=0\text{,}\) \(x_0= \frac{29}{4}\text{,}\) y las distancia tenemos
De lo cual tenemos
En el semiplano de Poincare.
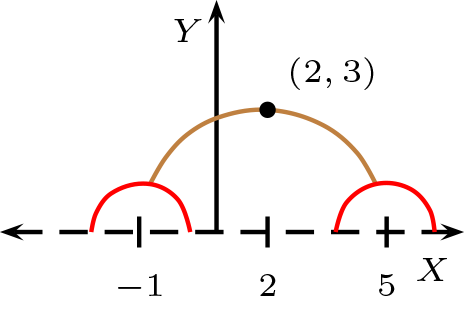
Dada la recta \(l:x^2+y^2=1\) y el punto \(P=(2,3)\text{.}\)
Determine las rectas paralelas hiperbólicas a la recta \(l\) y que pasa por \(P\text{.}\)
Grafiquemos la semicircunferencia unitaria de centro el origen y punto correspondiente.
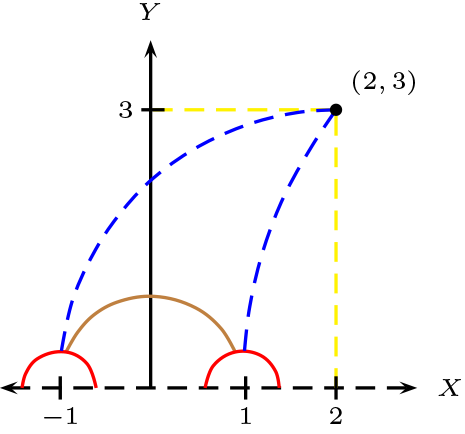
Notemos que existen posibles semicircunferencias y una semirecta paralela Por ello debe, tener ecuación
y debe pasar por los puntos \((2,3), (t,0)\text{,}\) \(t\in \mathbb{R}-]-1,1[\) y \(t\neq 2\) reemplazando obtenemos
sustituyendo obtenemos
De donde se concluye que
Además
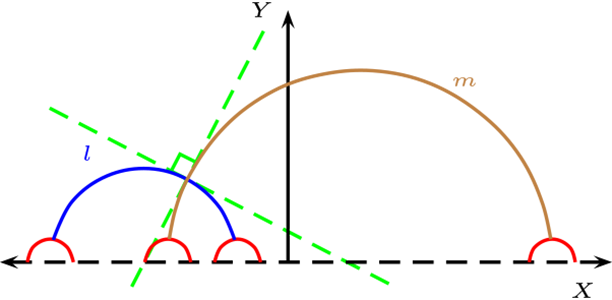
Relación de Paralelismo: Dos rectas son paralelas, si no tiene puntos en común, los 6 posibles caso son:
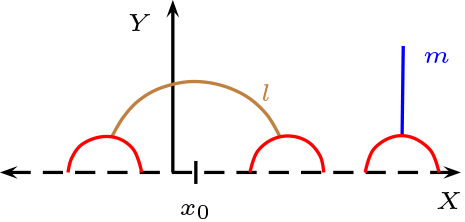
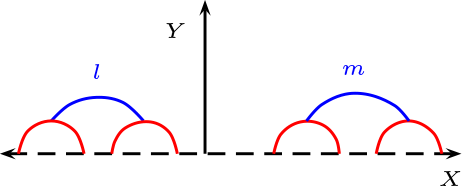
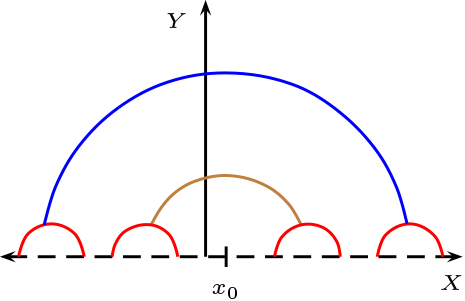

Relación de Ortogonalidad:
El ángulo entre un semirecta y una semicircunferencia en el punto de intersección corresponde a la recta tangente a la semicircunferencia con la semirecta en el punto de intersección y para el caso de dos semi circunferencia, es el ángulo entre las tangente a las circunferencias en el punto de intersección.
Las rectas \(l\) y \(m\) son perpendiculares en los siguientes casos
Una semicircunferencia con la semirecta \(l \perp m\)
Dos semi circunferencia \(l \perp m\)
En el semiplano de Poincare.
Dada la recta \(l:x^2+y^2=1\) y el punto \(P=(2,3)\text{.}\)
Determine las rectas ortogonales hiperbólicas a la recta \(l\) y que pasa por \(P\text{.}\)
Grafiquemos la semicircunferencia unitaria de centro el origen y punto correspondiente.
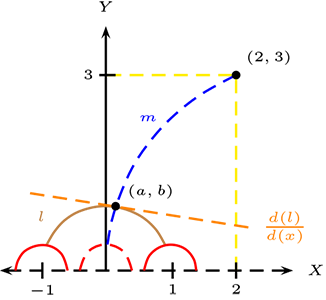
La recta ortogonal, sólo puede ser del tipo semicircunferencia, para ello sea \(m:(x-x_{0})^2+y^2=r^2\text{,}\) la recta solicitada.
Luego existe \(Q=(a,b)\) tal que \(P \mathcal{I} m\text{,}\) \(Q \mathcal{I} m, \) \(Q \mathcal{I} l\text{,}\) reemplazando tenemos:
Además deben ser perpendiculares, para ello calculemos la pendiente de la recta tangente en el punto \(Q\text{.}\)
luego tenemos,
Volvamos al sistema, igualando \(r^2\) obtenemos la siguiente igualdad
y reemplazando
Reemplazamos en la primera ecuación del sistema:
Finalmente tenemos la ecuación de la recta tangente a \(l\) es
En el semiplano de Poincare.
Dada la recta \(l:x^2+y^2=1\) y el punto \(P=(-5,8)\text{.}\)
Determine las rectas ortogonales hiperbólicas a la recta \(l\) y que pasa por \(P\text{.}\)
Notemos que el semiplano de Poincare, también se puede describir del siguiente modo
y las rectas están dadas por
Donde Re\((z) \) es la parte real de de \(z\) y Im\((z)\) es la parte imaginaria de \(z\)
Para determinar las simetrías de semiplano superior de Poincare, considere
y debemos tener presente que hay dos tipo de rectas en el Semiplano de Poincare
Caso 1: Simetría de eje la semirecta \(k:Re(z)=x_{0}\)
Recordemos la simetría respecto a la recta en el plano euclidiano
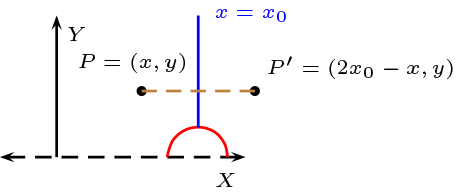
En nuestro caso tenemos
Caso 2: Simetría respecto a la semicircunferencia,
Veamos primero simetría respecto a la recta \(l:|z|=1\text{.}\)
Ya que \(|z|=1\text{,}\) luego tenemos que \(z \cdot \overline{z} = 1\text{,}\) de lo cual tenemos
es decir, la función \(R(z) = \frac{1}{\overline{z}}\) deja fijo los punto de la circunferencia unitaria.
\(R(z) = \frac{1}{z\overline{z}}z \text{,}\) luego si \(Im(z)>0\) entonces \(Im(R(z))>0 \text{,}\) ya que solo es amplificado por un número positivo.
\(R(R(z))= z\text{,}\) por ello se tiene que \(R^2=I\text{.}\)
Es una colineación.
Si \(k_a : x=a\neq 0\text{,}\) entonces \(R(l)= \{ (\frac{a}{a^2+y^2}, \frac{y }{a^2+y^2} )\ |\ y \geq 0\}\text{.}\)
Sean \(u= \frac{a}{a^2+y^2} , \ v= \frac{y}{a^2+y^2}\text{,}\) de lo cual obtenemos \(\frac{av}{u}= y \text{,}\) reemplazando tenemos
Es un circulo de centro \((\frac{1}{2a},0)\) y radio \(\frac{1}{2|a|}\text{.}\)
Cuando \(a=0\text{,}\) la recta queda fija.
Las semicircunferencia de centro \(a\) y radio \(r\text{,}\) tal que \(a^2\neq r^2\text{.}\)
Sea \(l: (x-a)^2+y^2= r^2\text{,}\) luego tenemos
Notemos que
Teniendo presente \(l: x^2+y^2= r^2-a^2+2ax\text{,}\) obtenemos que
Notemos que: Cuando \(a^2=r^2\text{,}\) la semicircunferencia es enviada en la semirecta \(l: x=\frac{1}{2a}\text{.}\)
Las semicircunferencia de centro el origen y radio \(r\text{,}\) son enviados en semicircunferencia de centro el origen y radio \(1/r\text{.}\)
Por el calculo anterior, se cumple la incidencia. Del mismo modo repasando cada caso, tenemos que preserva ortogonalidad
Por todo lo anterior tenemos que \(R(z)=\frac{1}{\overline{z}}\) es una simetría respecto al semicircunferencia unitaria, con centro en el origen.
Simetría respecto a la recta \(m:|z|=r\)
Consideremos las homotecia de centro \((0,0)\) y de razón \(r>0\text{.}\)
La cual respecta incidencia y ortogonalidad, es decir,
Por propiedad \ref{conj} tenemos que \(\sigma(a)=a'\text{,}\) entonces:
En nuestro caso tenemos que \(h_{r}(l)=m\text{,}\) entonces:
Consideremos el eje simetría \(t:|z-x_{0}|=r\)
La traslación en \(x_0\) respecta incidencia y ortogonalidad

Análogamente entonces se tiene
Sea \(R_l\) una simetría del plano de Poincare y \(a\in \mathbb{R}\text{,}\) entonces tenemos que
Si \(l: Re(z)=a \)
Si \(l: |z-a|=r\text{.}\)
Sea \(\Pi\) semiplano de Poincare y \(P=2+3i\text{.}\)
Determine un simétrica puntual \(H_P\text{,}\) respecto al punto \(P\text{.}\)
Sea \(H_{P}\) la simetría puntual, luego corresponde a una rotación en \(180^\circ\text{.}\)
Para ello debe existir \(a,b\in \mathcal{L}\) tales que
Consideremos la semicircunferencia \(b\) de centro 2 y radio 3 y \(a\) la semirecta vertical en \(Re(z)=2\text{.}\)
y satisface lo pedido
Sea \(\sigma\) una rotación de centro \(i\) y \(\sphericalangle 180^\circ\) en el semiplano de Poincare. Determine \(\sigma(z)\text{.}\)
Las rotaciones de centro \((0,1)\text{,}\) es compuesta de dos simetrías ortogonales que se intersecta en el punto \((0,1)\text{.}\)
De otro modo:
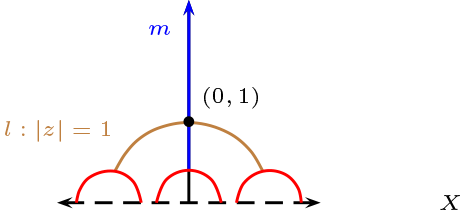
Podemos calcular de dos foma distintas
1. Si una es una semirecta \(m: Re(z) =0\) y \(l: |z|=1\) tenemos
Es una rotación en \(180^\circ\)
2. Si la dos recta son semicircunferencias:
Deben pasar por \((0,1)\) y perpendicular sera en \(180^\circ\)
Realizando la compuesta obtenemos
Notemos que
de este modo obtenemos la función anterior.
En el plano de Poincare
Determinar el grupo de rotaciones de centro en \(i\text{.}\)
Consideremos que usando traslación y homotecia siempre podemos considerar que una de las rectas es una semicircunferencia de radio 1 y centro en el origen, por el ejemplo anterior no consideramos el caso que la otra sea una semirecta.
donde \(i \mathcal{I}m\) es decir, \(1+a^2=r^2 \text{,}\) luego \(R_l\circ R_m \) es una rotación de centro \(i\text{.}\)
La rotación depende solo del valor de \(a\neq 0\text{,}\) y por el ejemplo anterior tenemos
Veamos la composición de dos rotaciones
Luego tenemos
Además \(\sigma_\infty \circ \sigma_a= \sigma_a \circ \sigma_\infty = \sigma_{\frac{-1}{a}} \)