Sección 1.1 Introducción
¶Un triple \(\Pi=(\mathcal{P},\mathcal{L},\mathcal{I})\text{,}\) se llama estructura de incidencia si y sólo si verifica \(\mathcal{P},\mathcal{L},\mathcal{I}\) conjuntos no vacío, \(\mathcal{P}\cap \mathcal{L}=\phi\) y \(\mathcal{I}\subseteq \mathcal{P}\times \mathcal{L}\text{.}\)
Notación
En el conjunto \(\mathcal{P}\text{,}\) sus elementos se llaman puntos y los designados con letra mayúscula \(P,Q,R\text{.}\) En el conjunto \(\mathcal{L}\text{,}\) sus elementos se laman rectas y los designados con letra minúscula \(l,m,t\) y la relación \(\mathcal{I}\) de incidencia entre puntos y rectas y denotamos por
\begin{equation*}
(P,l)\in \mathcal{I},\ P \text{ incide con } l,\ P \ \mathcal{I}\ l\qquad
(P,l)\not\in \mathcal{I},\ P \text{ no incide con } l,\ P \ {\not\mathcal{I}} \ l
\end{equation*}
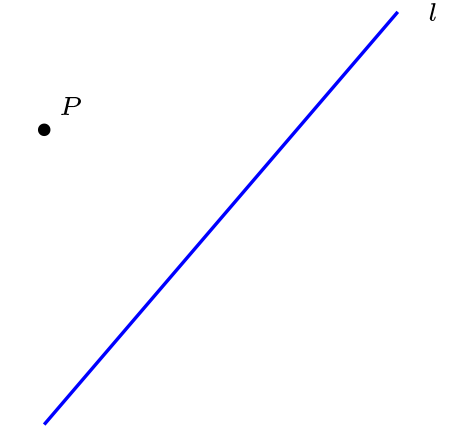
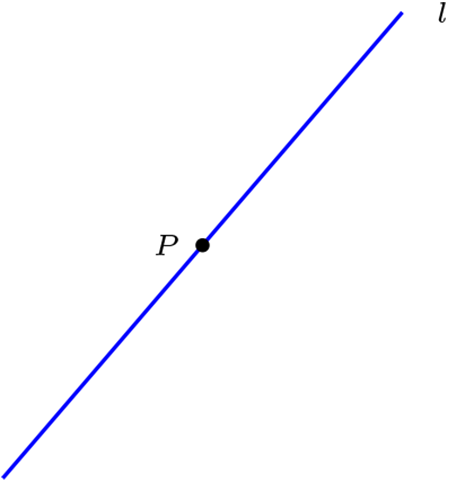
a) \(P \ {\not\mathcal{I}} \ l\text{,}\) \(\qquad P\) no incide con \(l\qquad \text{.}\) \(\qquad \qquad\) b) \(P \ \mathcal{I} l\text{,}\) \(\qquad P\) incide con \(l\text{.}\)
Notación
Dada \(l,m \in \mathcal{L}\)
\begin{equation*}
m \cap l \not= \phi \text{ si y sólo si }
(\exists P\in \mathcal{P}) ( P\mathcal{I}m \wedge P\mathcal{I}l)
\end{equation*}
o bien
\begin{equation*}
m \cap l = \phi \text{ si y sólo si }
(\forall P\in \mathcal{P}) ( P{\not\mathcal{I}} m \vee P{\not\mathcal{I}} l)
\end{equation*}
Definición 1.1.2
Sean \(l,m \in \mathcal{L}\text{.}\)
Se dice que \(l\) es paralela a \(m\) y se denota por \(l \parallel m\text{,}\) si y sólo si, \(m \cap l=\phi\ \vee\ l=m\text{.}\)