Sección 2.2 Plano Proyectivo y Plano Afín
¶Existen relaciones entre los planos afines y los planos proyectivos lo cual estudiaremos en esta sección.
Subsección 2.2.1 Plano Proyectivo en el Plano Afín
Dado un plano proyectivo, se puede construir un plano afín, del siguiente modo.
Sea \(\Pi = (\mathcal{P}, \mathcal{L}, \mathcal{I}) \) un plano proyectivo y \(l \in \mathcal{L}.\)
-
Los Puntos \(\overline{\mathcal{P}}\)
El conjunto de los puntos se definen del siguiente modo:
\begin{equation*} \overline{\mathcal{P}}= \{ P \in \mathcal{P}\ | \ P\not\mathcal{I} l \}= \mathcal{P}-l \end{equation*}de otro modo los puntos son, los puntos que no inciden en \(l\text{.}\)
-
Las Rectas \(\overline{\mathcal{L}}\)
Sea \(m \in \mathcal{L}-\{l\}\text{,}\) denotemos \(P_m \) el punto tal que \(m \cap l =\{P_m\}\)
\begin{equation*} m' = m-\{P_m\}= m- m\cap l \end{equation*}El conjunto de las rectas esta dado por:
\begin{equation*} \overline{\mathcal{L}}=\{ m' \ | \ m \neq l \} \end{equation*}es decir, las rectas, son las rectas \(m\) distintas de la recta \(l\) extrayendo el punto \(P_m\text{.}\)
-
La relación de Incidencia \(\overline{\mathcal{I}}\)
Sea \(P \in \overline{\mathcal{P}}, \ m \in \overline{\mathcal{L}}\text{.}\)
Se dice que \(P\) incide en \(m\text{,}\) lo que denotamos por \(P \overline{\mathcal{I}} m\text{,}\) si y sólo si \(P\mathcal{I}m\)
Consideremos el plano proyectivo minimal \(\mathbb{P}_2(\mathbb{Z}_2^3)\) y construimos ela estructura de incidencia dada anteriormente al omitir la recta
Sabemos que las rectas del plano proyectivos son:
que graficamos del siguiente modo
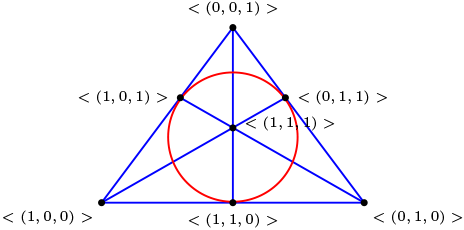
Luego obtenemos
Es un plano afín con cuatro punto y seis rectas, corresponde al plano afín minimal.
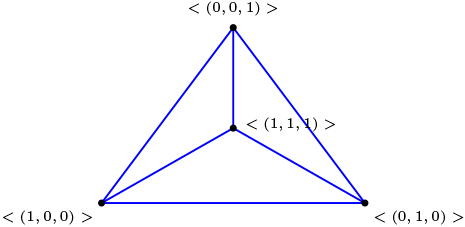
Teorema 2.2.2
\(\Pi^l=(\overline{\mathcal{P}}, \ \overline{\mathcal{L}},\ \overline{\mathcal{I}})\) es un plano afín.
Demostración
Veamos los axiomas de plano afín.
Axioma uno Si \(A,B \in \overline{\mathcal{P}}, A \neq B \) entonces \(\exists ! \ l \in \overline{\mathcal{L}}\) tal que \(A \ \overline{\mathcal{I}} \ l \text{ y } B \ \overline{\mathcal{I}} \ l\)
Si \(A,B \in \mathcal{P}, \ A \neq B\text{,}\) por axioma del plano proyectivo se tiene que existe única \(m \in \mathcal{L}\) tal que \(A \ \mathcal{I} \ m \text{ y } B \ \mathcal{I} \ m\text{,}\) la recta \(m \neq l\) ya que los puntos \(A\not\mathcal{I} l \) y \(B \not\mathcal{I} l\) luego se cumple.
Axioma dos Sean \(P \in \overline{\mathcal{P}}, m \in \overline{\mathcal{L}}, P \not\mathcal{I} m\) entonces existe \(m \parallel n \wedge P \mathcal{I}n\text{.}\)
Si \(m'= m \cup \{ P_m\}\text{,}\) con \(\ m' \in \mathcal{L}\text{,}\) luego tenemos la recta \(l_{P P_m}\in \mathcal{L}\text{,}\) claramente tenemos que \(l'= l_{P P_m}-\{P_m\} \in \overline{\mathcal{L}}\text{,}\) luego obtenemos
Axioma tres: Existe un triángulo.
En el plano afín \(\Pi\) existe cuadrángulo, los puntos \(A, B, C, D\) no son colineales. Si son cero o un punto en la recta \(l\) listo.
Si hay dos punto en la recta \(l\text{,}\) supongamos que son \(C, D\text{,}\) luego la recta \(L_{AC}\) tiene otro punto \(E\text{,}\) que no pertenece a \(l\text{,}\) \(A,B,E\) no son colineales. Toda recta tenia al menos tres puntos, luego ahora tiene al menos dos puntos, por lo tanto
Subsección 2.2.2 Plano Afín en el Plano Proyectivo
Dado un plano afín, se puede construir un plano proyectivo, de modo que el plano afín se inyecta en el proyectivo.
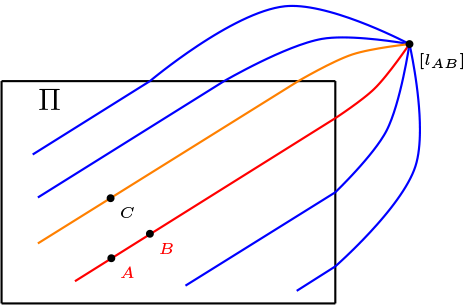
Sea \(\Pi=(\mathcal{P}, \ \mathcal{L},\ \mathcal{I})\) un plano afín, se construye el plano proyectivo del siguiente modo:
-
Los Puntos \(\overline{\mathcal{P}}\)
Sea \(l\in \mathcal{L}\text{,}\) denotamos por \([l]\) es el haz de rectas paralelas a \(l\text{.}\)
El conjunto de los puntos se definen del siguiente modo:
\begin{equation*} \overline{\mathcal{P}}= \mathcal{P} \cup \{ [l] \ | \ l \in \mathcal{L} \} \end{equation*}de otro modo los puntos son, los puntos anteriores unidos con los haces de rectas.
-
Las Rectas \(\overline{\mathcal{L}}\)
Dado \(m \in \mathcal{L}\text{,}\) tenemos que
\begin{equation*} \overline{m}=m \cup \{ [m] \} \end{equation*}y la recta \(l_{\infty}=\{ [l] \ | \ l \in \mathcal{L}\}\text{.}\)
El conjunto de las rectas esta dado por:
\begin{equation*} \overline{\mathcal{L}}=\{ \overline{m} \ | \ m \in \mathcal{L} \} \cup \{ l_{\infty} \} \end{equation*}es decir, las rectas, son las rectas del plano afín unido un punto que corresponde al haz de rectas paralelas a ella o bien la recta que contiene todos los haces de rectas paralelas.
-
La relación de Incidencia \(\overline{\mathcal{I}}\)
Sea \(P \in \overline{\mathcal{P}}, \ l \in \overline{\mathcal{L}}\text{.}\)
Se dice que \(P\) incide en \(l\text{,}\) lo que denotamos por \(P \overline{\mathcal{I}} l\text{,}\) si y sólo si una de las siguientes condiciones se satisface:
\(P \in \mathcal{P} \ \wedge \ l \in \mathcal{L} \ \wedge \ P \mathcal{I} l\)
\(P=[m] \ \wedge \ l \in \mathcal{L} \ \wedge \ m \parallel l\)
\(P=[m] \ \wedge \ l=l_{\infty}\)
Observación 2.2.3
Veamos primero un ejemplo antes de probar que es un plano proyectivo.
Ejemplo 2.2.4
Sea \(\mathcal{P}=\mathbb{Z}_{2}\times \mathbb{Z}_{2}\text{.}\) el plano afín minimal.
Construir el plano proyectivo, donde esta inyectado el plano afín
Las ecuaciones de las rectas de \(\mathbb{Z}_{2} \times \mathbb{Z}_{2}\) son
y los haces de rectas paralelas son:
representado por

En consecuencia, el plano proyectivo esta dado por
donde
Teorema 2.2.5
Sea \(\Pi=(\mathcal{P}, \ \mathcal{L},\ \mathcal{I})\) el plano afín, tal que se definen el conjunto de los puntos por:
y el conjunto de las rectas esta dado por:
y la relación de incidencia es la definida anteriormente entonces \(\overline{\Pi}=(\overline{\mathcal{P}}, \ \overline{\mathcal{L}},\ \overline{\mathcal{I}})\) es un plano proyectivo
Demostración
Veamos los axiomas de plano proyectivos.
Axioma uno Si \(A,B \in \overline{\mathcal{P}}, A \neq B \) entonces \(\exists ! \ l \in \overline{\mathcal{L}}\) tal que \(A \ \overline{\mathcal{I}} \ l \text{ y } B \ \overline{\mathcal{I}} \ l\)
Caso uno Si \(A,B \in \mathcal{P}, \ A \neq B\text{,}\) por axioma del plano afín se tiene que \(\exists! \ l \in \mathcal{L}\) tal que \(A \ \mathcal{I} \ l \text{ y } B \ \mathcal{I} \ l\text{,}\) luego se cumple.
-
Caso dos Si \(A \in \mathcal{P} \ \wedge \ [l] \in \overline{\mathcal{P}}\text{.}\)
Sea \(l \in [l]\) y \(A \not\mathcal{I} l\) entonces, por axioma dos del plano afín tenemos que \(\exists ! m \in \mathcal{L}\) tal que \(A \ \mathcal{I} \ m \text{ y } m \parallel l\) por lo tanto \(m \in [l]\) entonces \([l] \ \overline{\mathcal{I}} \ \overline{m}\) y \(A \ \overline{\mathcal{I}} \ \overline{m}\text{.}\)
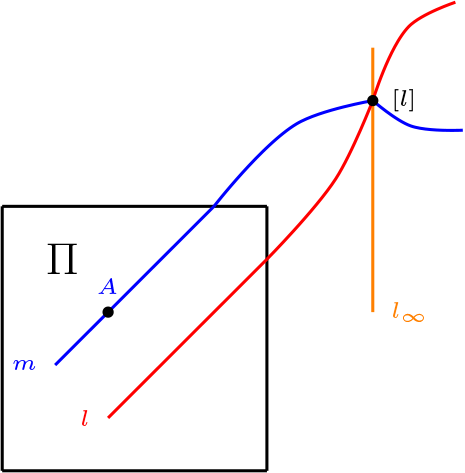
Caso tres \([l],[m] \in \overline{\mathcal{P}}\text{,}\) por definición \(\exists ! \ l_\infty \in \overline{\mathcal{L}}\) tal que \([l]\ \overline{\mathcal{I}} \ l_\infty [m] \ \overline{\mathcal{I}} \ l_{\infty}\)
Axioma dos Sean \(l,m \in \overline{\mathcal{L}}, l \neq m \) entonces \(l \cap m \neq \varnothing\text{.}\)
-
Caso uno: Si \(l= l' \cup \{[l']\}\) y \(m= m' \cup \{ [m']\}\text{,}\) con \(l', \ m' \in \mathcal{L}\text{.}\)
Si \(l' \parallel m'\text{,}\) luego tenemos que \([l']=[m']\text{,}\) por lo tanto \(l \cap m\neq \varnothing\text{.}\) En el otro caso, suponemos que \(l'\) no es paralela a \(m`\text{,}\) por ello tenemos que \(l' \cap m'\neq \varnothing\) y de lo cual se obtiene \(l \cap m \neq \varnothing \text{.}\)
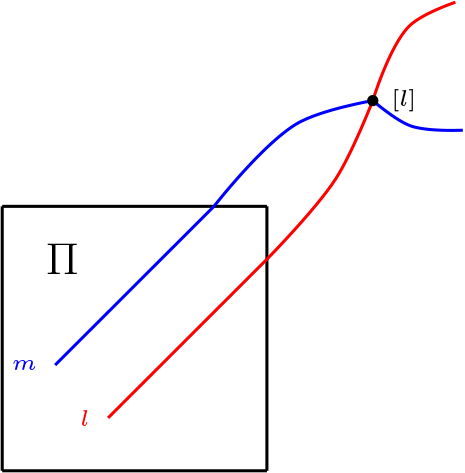
-
Caso dos: Sea \(l=l'\cup \{[l']\} \) y \(m= l_\infty \)
Por definición tenemos que \([l'] \overline{\mathcal{I}} l_\infty \ \wedge \ [l'] \overline{\mathcal{I}} l\text{,}\) de lo cual se obtiene
\begin{equation*} l \cap l_\infty \neq \varnothing \end{equation*}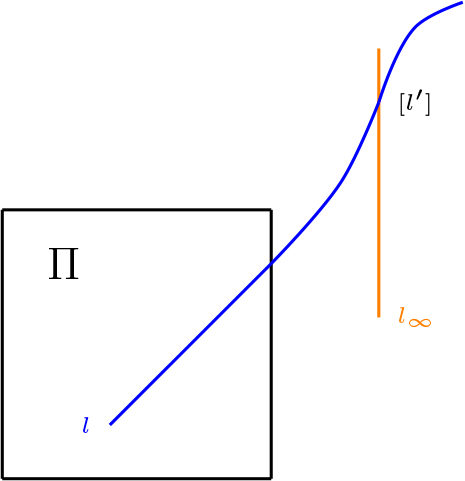
Axioma tres: Existe un cuadrángulo.
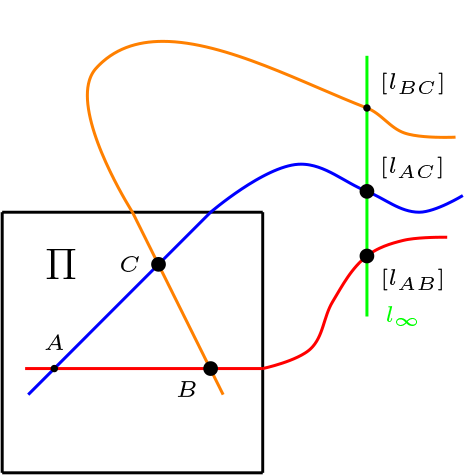
En el plano afín \(\Pi\) existe tres puntos \(A, B, C\) no colineales, consideremos los puntos \(C,B,[l_{AC}]\text{,}\) \([l_{AB}]\) ellos forman un cuadrángulo. Note que las rectas \(l_{AC}\) y la recta \(l_{AB}\) no son paralelas, luego a la única recta que pertenecen es \(l_\infty\) y las otras rectas son \(\overline{l_{CB}},\overline{l_{AC}}\) y \(\overline{l_{AB}}\text{,}\) todas distintas y no paralelas, por lo tanto
Por la construcción del Plano Proyectivo obtenemos el sumergimiento del Plano Afín
Observación 2.2.6
De esta manera entendemos que \(\Pi \subset \overline{\Pi}\text{.}\)
Subsección 2.2.3 Plano Afín Vectorial y el Plano Proyectivo Vectorial
Ahora veamos el caso especial, del Plano Afín Vectorial y el Plano Proyectivo Vectorial.
Sea \(\mathbb{K}\) un cuerpo y \(\Pi\) el plano afín asociado al espacio vectorial \(\mathbb{K} \times \mathbb{K}\text{,}\) donde los puntos son vectores, las rectas son rectas afines y la incidencia es la pertenecía.
Y el plano proyectivo esta dado por \(\mathbb{P}_2 (\mathbb{K}^3)= \overline{\Pi}=(\overline{\mathcal{P}},\ \overline{\mathcal{L}},\ \mathcal{I})\text{,}\) donde
y la incidencia es la contención.
Correspondencia entre Puntos
Sea \(\pi_0: z=0\) el plano \(XY\) y \(\pi_1: z=1\text{,}\) consideremos los siguientes conjuntos de punto y recta.
Para la construcción del plano proyectivo, en el plano afín, tenemos que agregar puntos, para ello a cada haz de rectas afines, escogemos como representante la recta vectorial, mirada en el plano \(\pi_0\text{,}\) de esta manera, el nuevo conjunto corresponde a los puntos en \(\pi_1\) unido a las rectas vectoriales en el plano \(\pi_0\text{.}\)
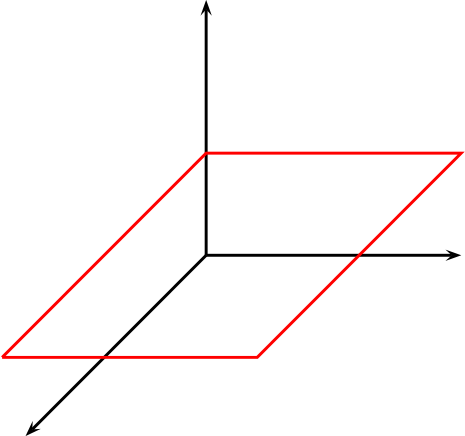
Notemos que la intersección de una recta vectorial con \(\pi_1\) es vacío, cuando la recta esta contenida en el plano \(XY\) o en caso contrario es un punto.
De esta manera tenemos la correspondencia entre puntos afines y proyectivos.
Correspondencia entre Rectas
Ahora veamos las rectas proyectiva. A cada recta del plano afín \(l:\lt (x,y)\gt +(a,b)\text{,}\) mirada en \(\pi_1\) corresponde a \(l':\lt (x,y,0)\gt +(a,b,1)\) agregamos la correspondiente recta vectorial en \(\pi_0\)
y el conjunto de todos los recta vectoriales en \(\pi_0\text{.}\)
La intersección de una plano vectorial con \(\pi_1\) es vacío, cuando la plano es el plano \(\pi_0\) o en caso contrario es una recta
La incidencia esta definida por la pertenecía
De esta manera tenemos \(\Pi'=(\mathcal{P}',\mathcal{L}',\mathcal{I}')\) es un plano afín, y existe una correspondencia biunívoca con el plano afín vectorial \(\Pi\text{.}\)
Ejemplo 2.2.7
En plano proyectivo \(\mathbb{P}_2(\mathbb{R}^3)\text{,}\) sean las rectas
i) Comprobar que tiene un punto en común.
ii) Al mirar las rectas en el Plano Afín, son paralelas
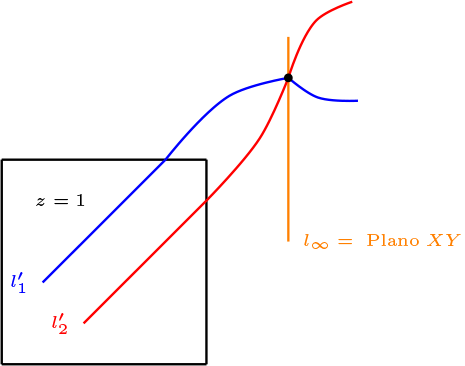
La intersección de ellas corresponde al sistema:
Notemos que \(l_1 \cap l_2\) es un punto en el plano proyectivo \(\lt (-3,2,0)\gt \text{,}\) contenido en el plano \(\pi_0\text{.}\)
En el plano afín, tenemos que realizar la intersección con el plano \(\pi_1:z=1\) y corresponde a dos rectas paralelas, y esta dada por
De lo cual tenemos que \(l_1' \parallel l_2'\text{.}\)
Ejemplo 2.2.8
Sean \(\Pi=\mathbb{R}^2\text{,}\) \(A=(2,3)\) y \(B=(-2,2)\text{.}\)
Encuentre la ecuación de la recta \(\overline{l_{AB}}\) en el plano proyectivo.
Veamos dos posibles desarrollos para determinar la ecuación.
Solución uno:
Entonces:
En donde se obtiene que la recta \(l_{AB}:x-4y=-10\text{,}\) del cual se obtiene la recta \(\overline{l_{AB}}: x-4y+10z=0\)
Solución dos:
En donde \(\overline{l_{AB}}=\left \langle (2,3,1),(-2,2,1) \right \rangle\) por lo tanto
luego los vectores son linealmente dependiente
Por lo tanto
