Teorema 4.9.1
Sea \(f: X \rightarrow X\) una dilatación en el Espacio Afín \((V,X,\cdot)\text{,}\) entonces \(f\) esta completamente determinada si se conoce la imagen de dos puntos.
Sección 4.9 Dilataciones en un Espacio Afín
¶Sea \((V,X,\cdot)\) un espacio afín, \(dim (X) \geq 2\) y la función \(f:X\rightarrow X\) biyectiva.
Recordemos que \(f\) es una dilatación si y sólo si, es una colineación que para todo \(l\) recta, \(f(l)\parallel l\)
Note que la identidad es una dilatación.
Definición 4.9.2
Sea \(f\) una dilatación en el espacio afín \((V,X,\cdot)\text{.}\)
Se dice que \(f\) es una Traslación si y sólo si , \(f\) no tiene puntos fijos o \(f=Id\text{.}\)
Se dice que \(f\) es una Homotecia si y sólo si , \(f\) tiene puntos fijos y el se llama centro de la homotecia o \(f=Id\text{.}\)
Teorema 4.9.3
Una traslación esta completamente determinada si se conoce la imagen de un punto.
Demostración
Sea f una traslación y \(a \in X\) tal que \(f(a)=a'\) y consideremos \(x \in X\text{.}\) de modo que \(x \ \not \in \ l_{aa'}\text{.}\)
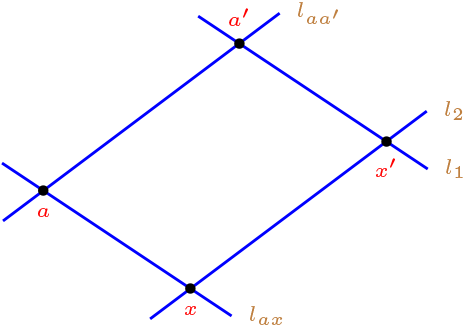
Definimos: \(l_2\) paralela a \(l_{aa'}\) y \(x \in \ l_2\)
\(l_1\) paralela a \(l_{ax}\) y \(a' \ \in \ l_1\)
Por lo tanto \(l_1 \cap l_2 = \{ x' \}\) es la imagen de \(x\text{.}\)
Al conocer la imagen de dos puntos, \(f\) esta completamente determinada.
Por argumentos similares a los realizados en el primer capitulo tenemos que las únicas traslaciones son \(t_{\overrightarrow{v}}\) con \(\overrightarrow{v}\in V\text{.}\)
Proposición 4.9.4
Sea \(f: X \rightarrow X\) una homotecia de centro \(c\in X\text{,}\) entonces existe \(k\in \mathbb{K}\) tal que
\begin{equation*}
f(x)= (k\overrightarrow{cx})\cdot c, \text{ Para todo } x\in X.
\end{equation*}
Demostración
Dado \(x \in X\text{,}\) distinto de \(c\text{,}\) luego \(f(x)\) no esta fijo, por ello tenemos que las rectas \(l_{cx} \parallel l_{cf(x)}\text{,}\) de este modo los vectores directores son linealmente dependiente \(\{\overrightarrow{cx}, \overrightarrow{cf(x)} \}\text{.}\)
Por lo anterior existe \(k \in \mathbb{K}\text{,}\) tal que \(\overrightarrow{cf(x)}=k \overrightarrow{c x}\text{.}\)
De este modo tenemos que \(f(x)= (k\overrightarrow{cx})\cdot c \text{.}\)
Ahora bien dado \(y \in X\text{,}\) tenemos que \(f(x)= (\alpha \overrightarrow{cy})\cdot c \text{,}\) pero notemos que \(l_{xy} \parallel l_{f(x)f(y)}\text{,}\) de este modo los vectores directores son linealmente dependiente \(\{\overrightarrow{xy}, \overrightarrow{f(x)f(y)} \}\text{,}\) de lo cual tenemos \(\alpha =k\)
\begin{equation*}
f(x)= (k\overrightarrow{cx})\cdot c, \text{ Para todo } x\in X.
\end{equation*}
Notación
\(M_{(c,k)}\) es la homotecia de razón \(k\) y centro \(c\text{.}\)
Proposición 4.9.5
Sea \((V,X,\cdot)\) un espacio afín entonces
\begin{equation*}
H_c=\{M_{(c,k)}\ | \ k \in \mathbb{K}^*\}
\end{equation*}
es un grupo, llamado de las homotecia de centro \(c\)
Demostración
Notemos solamente que
\begin{equation*}
M_{(c,k)}\circ M_{(c,t)}= M_{(c,kt)}
\end{equation*}
y
\begin{equation*}
M_{(c,k)}^{-1}=M_{(c,k^{-1})}
\end{equation*}
Ejemplo 4.9.6
Describa las homotecia de centro \(c\) y razón \(k\) en espacio vectorial afín.
\((V,V,\cdot)\text{,}\) el espacio vectorial afín,
\begin{equation*}
\begin{array}{rcl}
M_{(c,k)}(x) \amp=\amp (k\overrightarrow{cx})\cdot c \\
\amp=\amp (kx-kc)\cdot c \\
\amp=\amp (kx-kc)+ c \\
\amp=\amp kx+(1-k)c.
\end{array}
\end{equation*}
Teorema 4.9.7
Sea \(f\) una dilatación en espacio afín \((V,X,\cdot)\text{,}\) entonces existe \(\alpha \in \mathbb{K}\) tales que para todo \(x,y\in \text{,}\) se tiene
\begin{equation*}
\overrightarrow{f(x)f(y)} = \alpha \overrightarrow{xy}
\end{equation*}
\(\alpha\) se llama la razón de la dilatación
Demostración
Sea \(f\) una dilatación.
i) Si \(f\) es una traslación, luego \(f=t_{\overrightarrow{v}} \)
Lo cual se tiene que \(\alpha =1\text{.}\)
ii) Si \(f\) es una homotecia, luego \(f=M_{(c,k)} \)
Lo cual se tiene que \(\alpha =k\text{.}\)
Corolario 4.9.8
Sean \(f_1, f_2\) una dilatación en espacio afín \((V,X,\cdot)\text{,}\) de razón \(k_1, k_2\) respectivamente, entonces
\(f_1\circ f_2\) tiene razón \(k_1k_2\)
\(f_1^{-1}\) tiene razón \(k_{1}^{-1}\)
Corolario 4.9.9
Sea \((V,X,\cdot)\) un espacio afín, entonces
\begin{equation*}
D(X)/T(X) \simeq (\mathbb{K}^*,\cdot)
\end{equation*}
Proposición 4.9.10
Sea \((V,X,\cdot)\) un espacio afín.
Una dilatación esta completamente determinada si se conoce la imagen de un punto y la razón de la dilatación.
Demostración
Sea \(\sigma \) una dilatación de razón \(k\) tal que \(\sigma(c)=c'\)
Primer Caso, si \(\sigma \) es un traslación, \(k=1\text{,}\) y estamos listo.
\begin{equation*}
\sigma = t_{\overrightarrow{cc'}}
\end{equation*}
Segundo Caso, si \(\sigma\) es una rotación
\begin{equation*}
\sigma = M_{(a,k)}
\end{equation*}
Pero tenemos que determinar el centro
\begin{equation*}
\begin{array}{rcl}
M_{(a,k)}(c) \amp=\amp c' \\
k\overrightarrow{ac} \cdot a \amp=\amp c' \\
k\overrightarrow{ac} \amp=\amp \overrightarrow{ac'} \\
k\overrightarrow{ac} \amp=\amp \overrightarrow{ac+cc'} \\
k\overrightarrow{ac} -\overrightarrow{ac} \amp=\amp \overrightarrow{cc'} \\
(k-1)\overrightarrow{ca} \amp=\amp \overrightarrow{c'c} \\
\overrightarrow{ca} \amp=\amp\frac{1}{k-1} \overrightarrow{c'c} \\
a \amp=\amp\frac{1}{k-1} \overrightarrow{c'c}\cdot c
\end{array}
\end{equation*}
y la razón esta completamente determinado.
Proposición 4.9.11
Sea \((V,X,\cdot)\) un espacio afín y \(\sigma \) una dilatación tal que \(\sigma(x)=z\) y de la razón \(k\text{,}\) entonces
\begin{equation*}
\sigma= t_{\overrightarrow{xz}}\circ M_{(x,k)}
\end{equation*}
Demostración
\(\sigma \) una dilatación tal que \(\sigma(x)=z\) y de la razón \(k\text{.}\) Luego tenemos que
\begin{equation*}
t_{\overrightarrow{xz}}^{-1} \circ \sigma(x)=x
\end{equation*}
es una dilatación, que tiene un punto fijo y es de razón \(k\text{,}\) por lo tanto es una homotecia de razón \(k\)
\begin{equation*}
t_{\overrightarrow{xz}}^{-1} \circ \sigma = M_{(x,k)}
\end{equation*}
de lo cual tenemos
\begin{equation*}
\sigma= t_{\overrightarrow{xz}}\circ M_{(x,k)}
\end{equation*}
Proposición 4.9.12
Sea \((V,X,\cdot)\) un espacio afín, entonces para todo \(a,b \in V\text{,}\) para todo \(c\in X\) y para todo \(r, s\in K^*\)
\begin{equation*}
t_{\overrightarrow{a}}\circ M_{(c,r)}\circ t_{\overrightarrow{b}}\circ M_{(c,s)}= t_{\overrightarrow{a}+r\overrightarrow{b}}\circ M_{(c,rs)}
\end{equation*}
Demostración
Sean \(a,b \in V\text{,}\) \(c\in X\) y \(r, s\in \mathbb{K}^*\text{.}\)
\begin{equation*}
\begin{array}{rcl}
(M_{(c,r)}\circ t_{\overrightarrow{b}}\circ M_{(c,s)})(c) \amp=\amp M_{(c,r)}\circ t_{\overrightarrow{b}})((s\overrightarrow{cc}\cdot c)) \\
\amp=\amp M_{(c,r)}\circ t_{\overrightarrow{b}})(c) \\
\amp=\amp M_{(c,r)}(\overrightarrow{b}\cdot c)\\
\amp=\amp(r\overrightarrow{c(\overrightarrow{b}\cdot c)}\cdot c) \\
\amp=\amp(r\overrightarrow{b}\cdot c)) \\
\amp=\amp t_{r\overrightarrow{b}}(c)
\end{array}
\end{equation*}
De lo cual obtenemos que la dilatación
\begin{equation*}
t_{-r\overrightarrow{b}}\circ M_{(c,r)}\circ t_{\overrightarrow{b}}\circ M_{(c,s)}
\end{equation*}
tiene un punto fijo y la razón es el producto de las razones, luego es \(rs\text{.}\)
\begin{equation*}
t_{-r\overrightarrow{b}}\circ M_{(c,r)}\circ t_{\overrightarrow{b}}\circ M_{(c,s)}= M_{(c,rs)}
\end{equation*}
despejando obtenemos
\begin{equation*}
t_{\overrightarrow{a}}\circ M_{(c,r)}\circ t_{\overrightarrow{b}}\circ M_{(c,s)}= t_{\overrightarrow{a}+r\overrightarrow{b}}\circ M_{(c,rs)}
\end{equation*}
Subsección Ejercicios
Sea \((V,X,\cdot)\) un espacio afín, entonces
Determinar condiciones para \(c,d\in X\) distintos y \(r, s\in \mathbb{K}^*\) de modo que \(M_{(c,r)}\circ M_{(d,s)}\) es una traslación.