Geometría Afín

Notemos que \(\sigma \circ R_{a} \circ \sigma^{-1}\) es una simetría, ya que

1. \(\sigma \circ R_{a} \circ \sigma^{-1} \neq Id.\)

   Supongamos que \(\sigma \circ R_{a} \circ \sigma^{-1}=Id\) entonces

   \begin{equation*} \begin{array}{ccc} R_{a} \amp = \amp \sigma^{-1} \circ \sigma\\ R_{a} \amp = \amp Id \end{array} \end{equation*}

   Pues esto es una contradicción, por lo tanto es distinta a la identidad.

2. \((\sigma \circ R_{a} \circ \sigma^{-1})\circ (\sigma \circ R_{a} \circ \sigma^{-1})= Id\)

   Esto es verdadero pues \(Id=Id\text{,}\) de esta forma se cumple que tiene orden dos.

3. \(\sigma \circ R_{a} \circ \sigma^{-1}\) deja fijos a todos los puntos de la recta \(\sigma(a)\)

   Si \(P \mathcal{I} a \text{ entonces } \sigma{(P)} \mathcal{I} \sigma{(a)}\)

   \begin{equation*} (\sigma \circ R_{a} \circ \sigma^{-1})(\sigma(P))=\sigma(R_{a}(P))=\sigma{(P)} \end{equation*}

Luego tenemos que, es una simetría y fija los puntos de la recta \(\sigma(a)\) y

Sea \(\{P\}=a \cap b\text{,}\) luego tenemos que \(b\) es la única recta ortogonal a \(a\) en \(P\text{.}\) Además \(P \mathcal{I}a\) entonces \(R_{a}(P)=P\text{.}\)

Pero \(R_{a}(P) \mathcal{I} R_{a}(b)\) y \(R_{a}(b) \perp R_{a}(a)\text{,}\) de lo cual tenemos que:

Por unicidad de \(b\text{,}\) se tiene que \(R_{a}(b)=b\text{.}\)

Sea \(P \mathcal{I} b\) y \(P \not\mathcal{I} a\text{,}\) luego tenemos que \(R_a(P) \mathcal{I} b\text{,}\) consideremos \(c\) tal que \(P \mathcal{I} c\) y \(c\perp a\text{,}\) entonces por la propiedad anterior tenemos \(R_a(c) =c\text{,}\) de lo cual \(R_a(P) \mathcal{I} c\text{.}\)

De este modo tenemos que \(P, R_a(P) \mathcal{I} c\text{,}\) por ello tenemos \(c, b\) tiene dos puntos en común, luego las rectas son iguales, de lo cual obtenemos que \(b \perp a\text{.}\)

Sean \(a, b \in \mathcal{L}\) y \(a \perp b\text{,}\) luego tenemos que \(R_a(b)=b\text{,}\) además \(R^{-1}_a=R_a\text{,}\) de este modo tenemos que

despejando obtenemos

Supongamos ahora que

despejando, y usando la propiedad tenemos

luego \(R_a(b)=b\text{,}\) de lo cual \(a\perp b\text{.}\)

Ya que \(R_{c} \circ R_{b}\) es una rotaciones de centro \(P\) y consideremos \((R_{c} \circ R_{b})(a)=a'\text{,}\) entonces por axioma de rotación existe \(d \in \mathcal{L}\) tal que \(P \mthcal{I} d \text{ } \wedge \text{ }R_{c} \circ R_{b}|_{a}=R_{d} |_{a}\)

Notemos que

De lo cual obtenemos que

Supongamos que

de lo cual tenemos \(R_{c} \circ R_{b}=R_{d}\text{,}\) en donde

Análogamente \(d \perp c \text{.}\) Por lo tanto por \(P\) pasan dos rectas \(b,d\) perpendiculares a \(c\) esto es una contradicción, luego debe cumplirse la otra igualdad.

Ya que \(\sigma\) es una rotación, existen \(c,d \in \mathcal{L}\) tales que \(c \cap d = \{P\}\) y \(\sigma=R_{c} \circ R_{d}\)

Luego tenemos que \(P \mathcal{I}a,c,d\) y por teorema de las tres simetrías para rotación se obtiene

Despejando

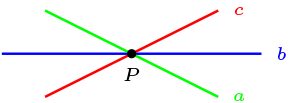
Clausura Sean \(\sigma _1 , \sigma_2 \in G_P\text{,}\) luego existen \(a,b,c,d\in \mathcal{L}\) tales que \(P\mathcal{I}a,b,c,d\) y \(\sigma_1= R_a\circ R_b\text{,}\) \(\sigma_2= R_c\circ R_d\text{.}\)

Como \(P\mathcal{I}a,b,c\) y \(R_a\circ R_b \circ R_c\text{,}\) por teorema de las tres simetrías existe \(l \in \mathcal{L}\) tal que \(P\mathcal{I}l\) y \(R_a\circ R_b \circ R_c =R_l\text{.}\)

Luego tenemos que

Neutro Dada \(a\in \mathcal{L}\) tal que \(P\mathcal{I}a\) entonces \(R_a\circ R_a =Id \in G_P\text{.}\)

Inverso Sea \(\sigma= R_a\circ R_b \in G_P\text{,}\) luego

Conmutatividad Sean \(\sigma_1= R_a\circ R_b\text{,}\) \(\sigma_2= R_c\circ R_d\text{.}\) Por demostrar que

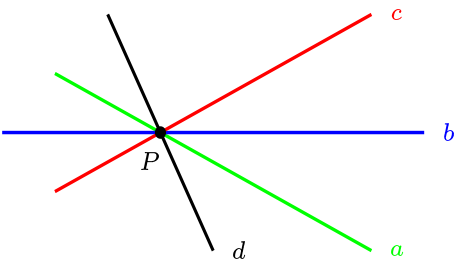
Por teorema de las tres simetrías tenemos que \(R_b\circ R_c \circ R_d =R_l\)

Luego \(\sigma_2 = R_b\circ R_l\text{.}\) De lo cual obtenemos

y

Reemplazando, obtenemos una proposición equivalente a que debemos demostrar

Pero por teorema de las tres simetrías, es una simetría

lo que demuestra lo requerido.

Ya que \(R_{c} \circ R_{b}\) es una traslación a lo largo de \(l\) y consideremos \((R_{c} \circ R_{b})(a)=a'\text{,}\) entonces por axioma de traslación existe \(d \in \mathcal{L}\) tal que \(d \perp l \text{ } \wedge \text{ }R_{c} \circ R_{b}|_{a}=R_{d} |_{a}\)

Notemos que

De lo cual obtenemos que

Supongamos que

de lo cual tenemos \(R_{c} \circ R_{b}=R_{d}\text{,}\) en donde

luego \(b \cap c \neq \varnothing \text{.}\)

Por lo tanto