Sección 4.4 Sistema de Coordenadas
¶Sean \((V,X,\cdot)\) un espacio afín, \(x_0\in X\) y \(B\) una base ordenada del espacio vectorial \(V\text{.}\)
Se dice que \((x_0,B)\) es un sistema de coordenada de \(X\) y las coordenada de \(x \in X\) respecto al sistema de coordenadas \((x_0,B)\text{,}\) están dadas por:
\begin{equation*}
[x]_{(x_{0},B)}=[\overrightarrow{x_{0}x}]_{B}
\end{equation*}
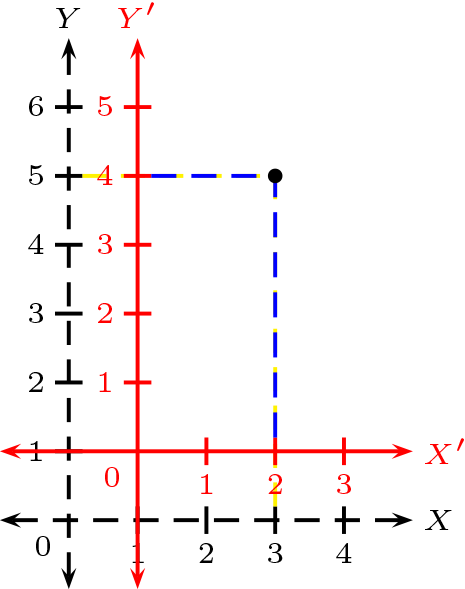
En espacio vectorial afín real, es decir, \(V=X=\mathbb{R}^2\text{.}\)
Sean \(x_{0}=(1,1)\) y \(B=\{(1,0),(0,1)\}\text{.}\)
Determine las coordenadas del punto \([(3,5)]_{(x_{0},B)}\)
\begin{equation*}
\begin{array}{rcl}
[(3,5)]_{(x_{0},B)} \amp = \amp[\overrightarrow{(1,1) (3,5)}]_{B} \\
\amp = \amp [ \overrightarrow{(3,5)-(1,1)}]_{B} \\
\amp = \amp [ \overrightarrow{(2,4)} ]_{B} \\
\end{array}
\end{equation*}
\begin{equation*}
\left[(3,5)\right]_{(x_{0},B)}=\left (\begin{array}{c}
2 \\
4
\end{array} \right)
\end{equation*}
Ejemplo 4.4.2
Sea \((V,X,\cdot )\) un espacio afín, \(x_{0} \in X\) y \(B=\{\overrightarrow{a_1},\overrightarrow{a_2}, \overrightarrow{a_3}, \cdots , \overrightarrow{a_n}\}\) base de \(V\text{.}\)
Determine las coordenadas de
\begin{equation*}
[(\overrightarrow{a_1}+\overrightarrow{a_2}+ \overrightarrow{a_3}+ \cdots + \overrightarrow{a_n})\cdot x_{0}]_{(x_{0},B)}
\end{equation*}
Sea
\begin{equation*}
\begin{array}{rcl}
\amp\amp [(\overrightarrow{a_{1}}+\overrightarrow{a_{2}}+\overrightarrow{a_{3}}+\cdots +\overrightarrow{a_{n}})\cdot x_{0}]_{(x_{0},B)} \\
\amp = \amp [\overrightarrow{x_{0} (\overrightarrow{a_{1}}+\overrightarrow{a_{2}}+\overrightarrow{a_{3}}+\cdots +\overrightarrow{a_{n}})\cdot x_{0}}]_{(B)} \\
\amp = \amp \left[\overrightarrow{a_{1}}+\overrightarrow{a_{2}}+\overrightarrow{a_{3}}+\cdots +\overrightarrow{a_{n}}\right]_B\\
\amp = \amp [\overrightarrow{a_{1}}]_{B}+[\overrightarrow{a_{2}}]_{B}+[\overrightarrow{a_{3}}]_{B}+\cdots + [\overrightarrow{a_{n}}]_{B} \\
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
\amp\amp [(\overrightarrow{a_{1}}+\overrightarrow{a_{2}}+\overrightarrow{a_{3}}+\cdots +\overrightarrow{a_{n}})\cdot x_{0}]_{(x_{0},B)}\\
\amp = \amp
\begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix}+
\begin{pmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{pmatrix}+ \ldots +
\begin{pmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{pmatrix}
\end{array}
\end{equation*}
\begin{equation*}
{[(\overrightarrow{a_{1}}+\overrightarrow{a_{2}}+\overrightarrow{a_{3}}+\cdots +\overrightarrow{a_{n}})\cdot x_{0}]_{(x_{0},B)} = \begin{pmatrix}
1 \\
1 \\
\vdots \\
1
\end{pmatrix}}
\end{equation*}
Teorema 4.4.3
Sean \((V,X,\cdot )\) un espacio afín, \(x_{0} \in X\) y \(B\) base de \(V\) tal que
\begin{equation*}
[\overrightarrow{v}]_{B} =\begin{pmatrix}
\alpha_{1} \\ \alpha_{2} \\ \vdots \\ \alpha_{n}
\end{pmatrix} \text{ y } [x]_{(x_0,B)}= \begin{pmatrix}
\beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{n}
\end{pmatrix} \text{, entonces }[\overrightarrow{v}\cdot x]_{(x_0,B)}=
\begin{pmatrix}
\alpha_{1}+\beta_{1} \\ \alpha_{2}+\beta_{2} \\ \vdots \\
\alpha_{n}+\beta_{n}
\end{pmatrix}
\end{equation*}
Demostración
\begin{equation*}
\begin{array}{ccc}
[\overrightarrow{v}\cdot x]_{(x_0,B)} \amp = \amp \left[ \overrightarrow{x_0 \left( \overrightarrow{v}\cdot x \right)} \right]_{B} \\
\amp = \amp \left[\overrightarrow{v}+\overrightarrow{x_0 x}\right]_{B} \\
\amp = \amp [\overrightarrow{v}]_{B}+[\overrightarrow{x_0 x}]_{B} \\
\amp = \amp [\overrightarrow{v}]_{B}+[x]_{(x_{0},B)}
\end{array}
\end{equation*}
De este modo se tiene
\begin{equation*}
[\overrightarrow{v}\cdot x]_{(x_{0},B)}=\begin{pmatrix}
\alpha_{1}+\beta_{1} \\
\alpha_{2}+\beta_{2} \\
\vdots \\
\alpha_{n}+\beta_{n}
\end{pmatrix}
\end{equation*}
Ejemplo 4.4.4
Sean \((V,X,\cdot)\) un espacio afín, \(x_{0}, x, y \in X\) y \(B\) una base de \(V\) tales que
\begin{equation*}
[x]_{(x_{0},B)}=\begin{pmatrix}
x_{1} \\ x_{2} \\ \vdots \\ x_{n}
\end{pmatrix}
\text{ y }
[y]_{(x_{0},B)}=\begin{pmatrix}
y_{1} \\
y_{2} \\
\vdots \\
y_{n}
\end{pmatrix}
\end{equation*}
Calcule \([\overrightarrow{xy}]_{B}\)
Si \(\overrightarrow{xy}=\overrightarrow{x x_{0}}+\overrightarrow{x_{0} y}=-\overrightarrow{x_{0} x}+\overrightarrow{x_{0} y}\text{,}\) entonces:
\begin{equation*}
\begin{array}{ccc}
[\overrightarrow{xy}]_{B} \amp = \amp [-\overrightarrow{x_{0} x}+\overrightarrow{x_{0} y}]_{B} \\
\amp = \amp -[\overrightarrow{x_{0} x}]_B+[\overrightarrow{x_{0} y}]_B \\
\amp = \amp -[\overrightarrow{x}]_{(x_{0},B)}+[\overrightarrow{y}]_{(x_{0},B)}
\end{array}
\end{equation*}
\begin{equation*}
[\overrightarrow{xy}]_{B}= \begin{pmatrix}
y_{1}-x_{1} \\ y_{2}-x_{2} \\ \vdots \\ y_{n}-x_{n}
\end{pmatrix}
\end{equation*}
Observación 4.4.5
Tener un sistema de coordenadas para el espacio afín \((V,X, \cdot)\) significa que podemos representar cada punto de \(X\) mediante una matriz columna.