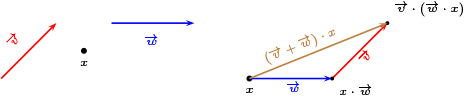[skip-to-content]

Sección 4.1 Introducción

El espacio afín, es un trio de la forma \((V,X,\cdot)\text{,}\) en donde:

  1. \(V\) es el espacio vectorial sobre el cuerpo \(\mathbb{K}\)

  2. \(X\) es el conjunto de puntos

  3. \(\cdot\) es una función dada por:

    \begin{equation*} \begin{array}{cccc} \cdot : \amp V \times X \amp \rightarrow \amp X \\ \amp (\overrightarrow{v},x) \amp \rightsquigarrow \amp \overrightarrow{v}\cdot x \end{array} \end{equation*}

    y cumple con:

    1. \(\left(\forall x \in X \right) \left( \overrightarrow{0}\cdot x = x \right)\)
    2. \(\left( \forall \overrightarrow{v},\overrightarrow{w} \in V \right) \left( \forall x \in X \right) \left( (\overrightarrow{v}+\overrightarrow{w})\cdot x=\overrightarrow{v}\cdot (\overrightarrow{w}\cdot x)\right)\)

    3. \(\left( \forall x,y \in X\right)\left(\exists! \text{ } \overrightarrow{xy}\in V \right) \left( \overrightarrow{xy}\cdot x =y \right)\) donde \(\overrightarrow{xy}\) es el unico vector que envia \(x \) en \(y\text{.}\)

Observación 4.1.1

Note que \(\cdot\) es una acción del grupo \((V,+)\) en el conjunto \(X\text{,}\) la cual es transitiva y fiel.

  1. Sean \(x \in X,\ \overrightarrow{v} \in V \)

    \begin{equation*} \overrightarrow{x \left( \overrightarrow{v} \cdot x \right)}\cdot x = \overrightarrow{v}\cdot x \end{equation*}

    Por unicidad son iguales

    \begin{equation*} \overrightarrow{x \left( \overrightarrow{v} \cdot x \right)}=\overrightarrow{v} \end{equation*}

  2. Sean \(x,y \in X,\ \ \overrightarrow{v} \in V\)

    \begin{equation*} \begin{array}{rcl} \left( \overrightarrow{xy}-\overrightarrow{v} \right)\left(\overrightarrow{v} \cdot x \right) \amp = \amp \overrightarrow{xy} \cdot \left( -\overrightarrow{v} \cdot \left( \overrightarrow{v} \cdot x \right) \right) \\ \amp = \amp \overrightarrow{xy} \cdot \left( \left( - \overrightarrow{v}+\overrightarrow{v}\right) \cdot x \right) \\ \amp = \amp \overrightarrow{xy}\cdot \left( \overrightarrow{0} \cdot x \right) \\ \left( \overrightarrow{xy}-\overrightarrow{v} \right)\left(\overrightarrow{v} \cdot x \right) \amp = \amp \overrightarrow{xy} \cdot x \\ \end{array} \end{equation*}

    Luego \(\left( \overrightarrow{xy}-\overrightarrow{v} \right) \left( \overrightarrow{v} \cdot x \right)= y\text{,}\) entonces

    \begin{equation*} \overrightarrow{xy}-\overrightarrow{v}=\overrightarrow{\left( \overrightarrow{v} \cdot x \right)y} \end{equation*}

    De lo cual se tiene (e)

    \begin{equation*} \overrightarrow{y \left( \overrightarrow{v} \cdot x \right)}=\overrightarrow{yx}+\overrightarrow{v} \end{equation*}

  3. Sean \(\overrightarrow{v} \in V, \ \ x,y \in X \)

    \begin{equation*} \begin{array}[b]{rcl} \overrightarrow{w} \amp = \amp \overrightarrow{\left( \overrightarrow{v}\cdot x \right)\left( \overrightarrow{v} \cdot y \right)} \\ \overrightarrow{w}\cdot \left( \overrightarrow{v} \cdot x \right) \amp = \amp \overrightarrow{\left( \overrightarrow{v}\cdot x \right)\left( \overrightarrow{v} \cdot y \right)} \cdot \left( \overrightarrow{v} \cdot x \right) \\ \overrightarrow{w}\cdot \left( \overrightarrow{v} \cdot x \right) \amp = \amp \overrightarrow{v} \cdot y \\ -\overrightarrow{v}\cdot \left(\overrightarrow{w}\cdot \left( \overrightarrow{v} \cdot x \right) \right) \amp = \amp - \overrightarrow{v} \cdot \left( \overrightarrow{v} \cdot y \right) \\ \left( - \overrightarrow{v}+ \overrightarrow{w}+\overrightarrow{v} \right)\cdot x \amp = \amp \left( -\overrightarrow{v}+\overrightarrow{v} \right) \cdot y \\ \overrightarrow{w} \cdot x \amp = \amp y \\ \overrightarrow{w} \amp = \amp \overrightarrow{xy} \end{array} \end{equation*}

  4. Sean \(\overrightarrow{v} \in V\text{,}\) \(x\in X\) tales que \(\overrightarrow{v}\cdot x= x \text{,}\) pero \(\overrightarrow{0}\cdot x= x \) luego tenemos que

    \begin{equation*} \overrightarrow{v} = \overrightarrow{xx}= \overrightarrow{0} \end{equation*}