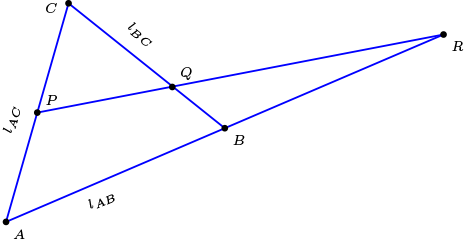
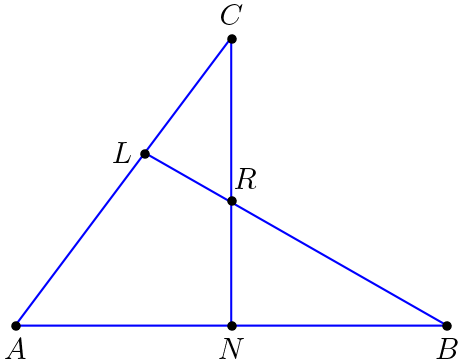
Apliquemos el teorema de Menelao a los siguientes casos
Luego tenemos
\begin{equation*}
(L,C,A)(P,N,C)(B,A,N)=1, \qquad
(M,C,B)(P,N,C)(A,B,N)=1
\end{equation*}
Teniendo presente la propiedad \ref{rafin}, y la hipótesis se obtiene \(\lambda= (L,A,C),\ \mu=(P,N,C),\ \alpha=(B,A,N)\text{,}\) luego
\begin{equation*}
(L,C,A)= \frac{1}{\lambda},\ (B,A,N)=\frac{1}{1- \alpha},\ (A,B,N)= \frac{\alpha}{\alpha -1}
\end{equation*}
Reemplazando
\begin{equation*}
\frac{1}{\lambda}(P,C,N)\frac{1}{1- \alpha}=1, \qquad
\mu (P,C,N)\frac{\alpha}{\alpha- 1}=1
\end{equation*}
Concluimos despejando e igualando obtenemos
\begin{equation*}
(P,C,N)= \lambda(1-\alpha)=\frac{(\alpha- 1)}{\alpha\mu}
\end{equation*}
Así obtenemos
\begin{equation*}
\alpha\lambda\mu= \frac{\alpha-1}{1-\alpha}=-1
\end{equation*}
En la otra dirección, Suponemos \(\alpha\lambda\mu=-1\) y
\begin{equation*}
l_{AM}\cap l_{BL}=P \qquad l_{AM}\cap l_{CN}=Q \qquad l_{BL}\cap l_{CN}=R.
\end{equation*}
Apliquemos el teorema de Menelao a los siguientes casos
\begin{equation*}
(L,C,A)(R,N,C)(B,A,N)=1, \qquad
(M,C,B)(Q,N,C)(A,B,N)=1
\end{equation*}
Teniendo presente la propiedad \ref{rafin}, y la hipótesis se obtiene \(\lambda= (L,A,C),\ \mu=(P,N,C),\ \alpha=(B,A,N)\text{,}\) luego
\begin{equation*}
(L,C,A)= \frac{1}{\lambda},\ (B,A,N)=\frac{1}{1- \alpha},\ (A,B,N)= \frac{\alpha}{\alpha -1}
\end{equation*}
Reemplazando
\begin{equation*}
\frac{1}{\lambda}(R,C,N)\frac{1}{1- \alpha}=1, \qquad
\mu (Q,C,N)\frac{\alpha}{\alpha- 1}=1
\end{equation*}
Despejando y reemplazando el \(\mu=\frac{-1}{\alpha\lambda} \)
\begin{equation*}
(R,C,N)=\lambda(1- \alpha) , \qquad
(Q,C,N)=\frac{\alpha- 1}{\mu \alpha}=\lambda(1- \alpha)
\end{equation*}
Los puntos esta a una misma razón afín luego son iguales.