Sección 1.7 Dilataciones en un Plano Afín Vectorial
¶Recordemos que \(V\) un \(\mathbb{K}\) espacio vectorial de dimension dos y el plano afín esta formado por \(\mathcal{P}= V, \ \mathcal{L}=\{ \text{ rectas afines } \}\) y la incidencia es la pertenencia.
1. Traslaciones: \(f\in \mathcal{T}(V)\text{.}\)
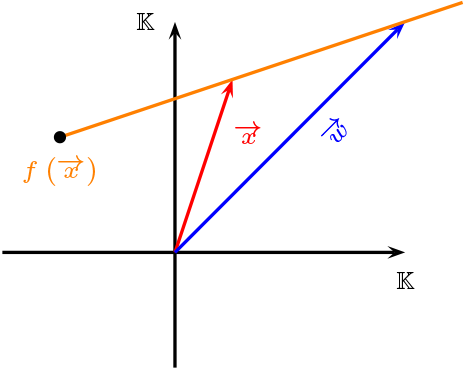
Sea \(\overrightarrow{v}=f(\overrightarrow{0})\text{,}\) aplicando el Teorema \ref{t-tras} tenemos que, si \(\overrightarrow{x}\) linealmente independiente con \(\overrightarrow{v}\text{,}\) la imagen se obtiene de la intersección de las rectas
\begin{equation*}
l_1: \lt \overrightarrow{v}\gt+ \overrightarrow{x}, \ \ l_2: \lt\overrightarrow{x}\gt+ \overrightarrow{v}
\end{equation*}
cuya intersección es \(\overrightarrow{x}+ \overrightarrow{v}\) de esta forma tenemos que, \(f(\overrightarrow{x})=\overrightarrow{x}+\overrightarrow{v}\) una traslación en \(\overrightarrow{v}\text{.}\)
Luego en general las traslaciones son funciones de la forma:
\begin{equation*}
\begin{array}{rccl}
f:\amp V \amp \longrightarrow \amp V \\
\amp \overrightarrow{x} \amp\rightsquigarrow \amp f(\overrightarrow{x})= \overrightarrow{x} + \overrightarrow{v}
\end{array}
\end{equation*}
Notación
\(\mathcal{T}(V)=\{t \in \mathcal{D}(\Pi) \ | \ t \text{ es una traslación} \}\text{,}\) es decir, si \(t \in \mathcal{T}(V)\text{,}\) entonces existe un vector \(\overrightarrow{v}\text{,}\) tal que \(t(\overrightarrow{x})=\overrightarrow{x}+ \overrightarrow{v}\text{,}\) incluimos el vector nulo \(\overrightarrow{0}\) de las traslaciones posibles.
Proposición 1.7.1
Sea \(t \in \mathcal{T}(V)\text{,}\) tal que \(t(\overrightarrow{x})=\overrightarrow{x}+ \overrightarrow{v}\text{,}\) entonces
\begin{equation*}
t^{-1}(\overrightarrow{x})=\overrightarrow{x}-\overrightarrow{v}
\end{equation*}
Demostración
Sea \(\overrightarrow{x},\overrightarrow{y} \in V\) tal que:
\begin{equation*}
\begin{array}{rcll}
\overrightarrow{y}\amp=\ampt^{-1}(\overrightarrow{x})\amp / \cdot t (izq.)\\
t(\overrightarrow{y}) \amp = \amp \overrightarrow{x} \amp \\
\overrightarrow{y}+ \overrightarrow{v} \amp = \amp \overrightarrow{x} \amp / +(-\overrightarrow{v}) \\
\overrightarrow{y} \amp = \amp \overrightarrow{x}- \overrightarrow{v}
\end{array}
\end{equation*}
Por lo tanto \(t^{-1}(\overrightarrow{x})=\overrightarrow{x}- \overrightarrow{v}\)
También se puede designara a la traslación de vector \(\overrightarrow{v}\) como \(t_{\overrightarrow{v}}\)
\(t_{\overrightarrow{v}}^{-1}(\overrightarrow{x})=t_{- \overrightarrow{v}}(\overrightarrow{x})\)Composición de traslaciones: Sea \(t_{\overrightarrow{v}},t_{\overrightarrow{w}} \in \mathcal{T}(V)\)
\begin{equation*}
\begin{array}{rcl}
(t_{\overrightarrow{v}} \circ t_{\overrightarrow{w}})(\overrightarrow{x}) \amp = \amp t_{\overrightarrow{v}}(\overrightarrow{x}+\overrightarrow{w})\\
\amp = \amp (\overrightarrow{x}+ \overrightarrow{w})+ \overrightarrow{v} \\
\amp = \amp \overrightarrow{x}+(\overrightarrow{w}+\overrightarrow{v}) \\
\amp = \amp t_{\overrightarrow{v}+\overrightarrow{w}}(\overrightarrow{x})
\end{array}
\end{equation*}
Proposición 1.7.2
\((\mathcal{T}(V),\circ)\) es un grupo abeliano, isomorfo a \((V,+)\)
Subsección Ejercicios
Sea \(\Pi\) un plano afín vectorial, \(t \) una traslación y \(f \in \mathcal{D}(\Pi) \)
Demostrar que \(f\circ t \circ f^{-1}\) es una traslación
2. Homotecias:
Sea \(f \in D(\Pi)\) una homotecia, luego existe \(\overrightarrow{w}\) tal que \(f(\overrightarrow{w})=\overrightarrow{w}\text{.}\)
Sea \(\overrightarrow{x} \in V\text{,}\) y \(l \in \mathcal{L}\text{,}\) tal que \(\overrightarrow{x},\overrightarrow{w} \in l\text{,}\) sabemos que \(f(l) \parallel l\text{,}\) y \(f(\overrightarrow{x}), \overrightarrow{w} \in f(l)\) y \(\overrightarrow{x},\overrightarrow{w} \in l\text{.}\)
Por lo tanto \(\{\overrightarrow{x}-\overrightarrow{w},\ f(\overrightarrow{x})-\overrightarrow{w}\}\) son linealmente dependiente, entonces:
\begin{equation*}
\begin{array}{rcll}
f(\overrightarrow{x})-\overrightarrow{w} \amp = \amp \alpha (\overrightarrow{x}- \overrightarrow{w}) \\
f(\overrightarrow{x}) \amp = \amp \alpha \overrightarrow{x}- \alpha \overrightarrow{w}+ \overrightarrow{w}\\
f(\overrightarrow{x}) \amp = \amp \alpha \overrightarrow{x}+(1-\alpha)\overrightarrow{w} \\
\end{array}
\end{equation*}
con \(1\neq \alpha \neq 0\text{.}\)
Al considerar el teorema 8, y sabiendo que conocemos la imagen de \(\overrightarrow{w}\text{,}\) \(\overrightarrow{x}\text{,}\) para determinar la imagen de otro punto no colineal con \(\overrightarrow{x},\overrightarrow{w}\text{,}\) tenemos trazar la recta \(l_1\) paralela a \(l_{\overrightarrow{x}\overrightarrow{z}}\) que pasa por \(f(\overrightarrow{x})\) y la recta \(l_2=l_{\overrightarrow{x}\overrightarrow{z}}\) y la intersección es la imagen de \(\overrightarrow{z}\)
Luego los vectores
\(\{\overrightarrow{z}-\overrightarrow{x}, f(\overrightarrow{z})-f(\overrightarrow{x})\}, \ \{\overrightarrow{x}-\overrightarrow{w}, f(\overrightarrow{x})-f(\overrightarrow{w})\},\ \{\overrightarrow{z}-\overrightarrow{w}, f(\overrightarrow{z})-f(\overrightarrow{w})\},\)
también son linealmente dependiente, de lo cual se obtiene
\begin{align*}
\alpha(\overrightarrow{x}-\overrightarrow{w}) \amp=\amp f(\overrightarrow{x})-f(\overrightarrow{w}) \\
\alpha_1(\overrightarrow{z}-\overrightarrow{x}) \amp=\amp f(\overrightarrow{z})-f(\overrightarrow{x}) \\
\alpha_2(\overrightarrow{z}-\overrightarrow{w}) \amp=\amp f(\overrightarrow{z})-f(\overrightarrow{w})
\end{align*}
Igualando obtenemos
\begin{equation*}
\alpha(\overrightarrow{x}-\overrightarrow{w})+\alpha_1(\overrightarrow{z}-\overrightarrow{x}) - \alpha_2(\overrightarrow{z}-\overrightarrow{w})=0
\end{equation*}
reordenando tenemos
\begin{equation*}
(\alpha- \alpha_1)(\overrightarrow{x}-\overrightarrow{w}) +(\alpha_1- \alpha_2)(\overrightarrow{z}-\overrightarrow{w})=0
\end{equation*}
Como los puntos son no colineales luego los vectores son linealmente independiente (solución única)
\begin{equation*}
\alpha = \alpha_1=\alpha_2
\end{equation*}
El otro caso, es análogo.
Por ello, existe un único \(\alpha\) y \(\overrightarrow{w}\text{.}\)
Definición 1.7.3
Sea \(f:V\rightarrow V\) una homotecia, dada por
\begin{equation*}
h_{\alpha, \overrightarrow{w}}(\overrightarrow{x})= \alpha \overrightarrow{x}+(1-\alpha)\overrightarrow{w}.
\end{equation*}
Se dice que, \(\alpha\) es la razón de la homotecia y \(\overrightarrow{w}\) es el centro de la homotecia.
Proposición 1.7.4
Sea \(f:V\rightarrow V\) una homotecia, tal que
\begin{equation*}
f(\overrightarrow{x})= \alpha \overrightarrow{x}+(1-\alpha)\overrightarrow{w}.
\end{equation*}
entonces
\begin{equation*}
f^{-1}(\overrightarrow{x})=\frac{1}{\alpha} \overrightarrow{x}+\left( 1-\frac{1}{\alpha} \right) \overrightarrow{w}
\end{equation*}
Demostración
Sea \(f^{-1}(\overrightarrow{x})= \overrightarrow{y}\text{,}\) entonces:
\begin{equation*}
\begin{array}{rcll}
\overrightarrow{y} \amp = \amp f^{-1}(\overrightarrow{x}) \amp / \circ f \\
f(\overrightarrow{y}) \amp = \amp \overrightarrow{x} \amp \\
\alpha \overrightarrow{y}+(1-\alpha)\overrightarrow{w} \amp = \amp \overrightarrow{x} \amp /+(\alpha -1)\overrightarrow{w}) \\
\alpha \overrightarrow{y} \amp = \amp \overrightarrow{x}+(\alpha-1)\overrightarrow{w} \amp / \frac{1}{\alpha}\\
\overrightarrow{y} \amp = \amp \frac{1}{\alpha}\overrightarrow{x}+\left( 1- \frac{1}{\alpha} \right) \overrightarrow{w}
\end{array}
\end{equation*}
Por ello tenemos
\begin{equation*}
f^{-1}(\overrightarrow{x})=\frac{1}{\alpha} \overrightarrow{x}+\left( 1-\frac{1}{\alpha} \right) \overrightarrow{w}
\end{equation*}
Composición de homotecias de centro \(\overrightarrow{w}\text{:}\)
Sea \(f_{1},f_{2}\) dos homotecias de centro \(\overrightarrow{w}\text{,}\) entonces tenemos que:
\begin{equation*}
\begin{array}{rcl}
f_{1}(\overrightarrow{x}) \amp = \amp \alpha \overrightarrow{x}+(1-\alpha)\overrightarrow{w}\\
f_{2}(\overrightarrow{x}) \amp = \amp \beta \overrightarrow{x}+ (1-\beta)\overrightarrow{w}\\
\amp \amp \\
(f_{1}\circ f_{2})(\overrightarrow{x}) \amp = \amp f_{1}(\beta \overrightarrow{x}+(1-\beta)\overrightarrow{w})\\
\amp = \amp \alpha (\beta \overrightarrow{x}+(1-\beta)\overrightarrow{w})+(1-\alpha)\overrightarrow{w}\\
\amp = \amp \alpha \beta \overrightarrow{x}+\alpha \overrightarrow{w}-\alpha \beta \overrightarrow{w}+\overrightarrow{w}-\alpha \overrightarrow{w}\\
\amp = \amp \alpha \beta \overrightarrow{x}+(1-\alpha \beta)\overrightarrow{w}
\end{array}
\end{equation*}
La composición de homotecias del mismo centro es otra homotecia del mismo centro y con razón el producto de las razones respectivas de las homotecias.
Definimos:
Sea
\begin{equation*}
\mathcal{H}_{\overrightarrow{0}}=\{f \in D(\Pi)\ |\ f(\overrightarrow{0})=\overrightarrow{0}\}
\end{equation*}
\begin{equation*}
\mathcal{H}_{\overrightarrow{w}}=\{f \in D(\Pi) \ | \ f(\overrightarrow{w})=\overrightarrow{w}\},
\end{equation*}
en donde \(\mathcal{H}_{\overrightarrow{0}}\) es el conjunto de la homotecia de centro \(\overrightarrow{0}\text{,}\) incluida la identidad.
\((\mathcal{H}_{\overrightarrow{0}}, \circ)\) se denomina grupo de las homotecias de centro \(\overrightarrow{0}\text{.}\)
\begin{equation*}
(\mathcal{H}_{\overrightarrow{0}},\circ) \cong (\mathbb{K}^*, \cdot)
\end{equation*}
Subsección Ejercicios
Sea \(\Pi\) el plano afín vectorial, entonces
Demostrar que
\begin{equation*}
\mathcal{H}_{\overrightarrow{0}}\simeq \mathcal{H}_{\overrightarrow{w}}
\end{equation*}
Forma General de una dilatación en un Plano Afín Vectorial
Note que toda dilatación es compuesta de traslaciones y homotecias.
Sea \(f\in D(\Pi)\text{,}\) entonces existen \(\alpha \neq 0\) y \(\overrightarrow{v}\in V\)
\begin{equation*}
f_{\alpha,\overrightarrow{v}}(\overrightarrow{x})=\alpha\overrightarrow{x}+\overrightarrow{v}=f(\overrightarrow{x})
\end{equation*}
Proposición 1.7.7
En el plano afín vectorial \(V\text{.}\)
\begin{equation*}
D(V)=\mathcal{T}(V) \circ \mathcal{H}_{\overrightarrow{0}}(V)
\end{equation*}
Ejemplo 1.7.8
Sea
\begin{equation*}
\begin{array}{ccccl}
T \amp : \amp \mathbb{R}^2 \amp \rightarrow \amp \mathbb{R}^2 \\
\amp \amp (x,y) \amp \rightarrow \amp (y,x)+(1,1)
\end{array}
\end{equation*}
Determine \(F \in \mathcal{D}(\mathbb{R}^2)\text{ tal que } T \circ F = F \circ T \)
Sea \(F\) una dilatación luego existen \(\alpha \in \mathbb{R}\) no nulo,\((a,b)\in \mathbb{R}^2\) tal que
\begin{equation*}
F(x,y)=\alpha(x,y)+(a,b),\ \ \forall (x,y)\in \mathbb{R}^2
\end{equation*}
Veamos la compuesta
\begin{equation*}
\begin{array}{rcl}
(T \circ F)(x,y) \amp = \amp (F \circ T)(x,y) \\
T(\alpha x+a,\alpha y +b) \amp = \amp F(y+1,x+1) \\
(\alpha y +b +1, \alpha x + a +1) \amp = \amp (\alpha y + \alpha +a,\alpha x + \alpha +b)
\end{array}
\end{equation*}
Igualando coordenada
\begin{equation*}
\begin{array}{rcl|}
b+1 \amp = \amp \alpha +a \\
a+1 \amp = \amp \alpha +b \\
\hline
\end{array}
\end{equation*}
del cual se obtiene \(a=b\) y \(\alpha = 1\text{,}\) por lo tanto \(F\) es una traslación de la forma
\begin{equation*}
F(x,y)=(x+a,y+a)
\end{equation*}