Proposición 1.4.1
Con las notaciones anteriores \(\Pi=(\mathbb{R}^2, \mathcal{L},\mathcal{I})\) es un plano afín, llamado plano de Moulton.
Sección 1.4 Plano de Moulton
¶El Plano de Moulton se construye en el articulo "Forestra y Moulton, A simple non-Desarguesian plane geometry. Trans. Am. Math. Soc, 3:192-95`` y es un ejemplo de un Plano Afín no trivial.
Consideremos el conjunto de puntos del plano afín \(\mathcal{P}=\mathbb{R}^2\text{,}\) los puntos del plano euclidianos.
Ahora veamos las rectas que constituye el conjunto \(\mathcal{L}\text{,}\) son de cuatro tipos:
-
Las rectas de pendiente positiva \(\left ( m>0\right )\) en el plano \(\mathbb{R}^2\text{.}\)
-
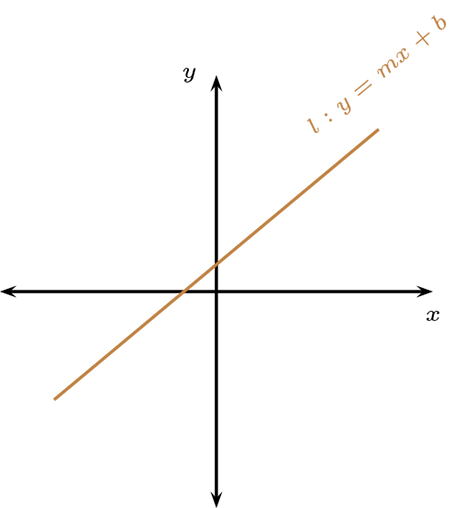
Las rectas con pendiente igual a cero o infinita en el plano \(\mathbb{R}^2\text{.}\)
-
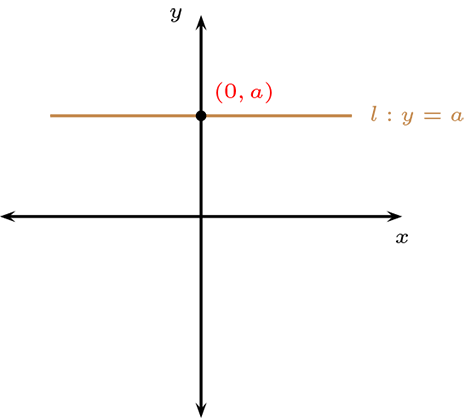
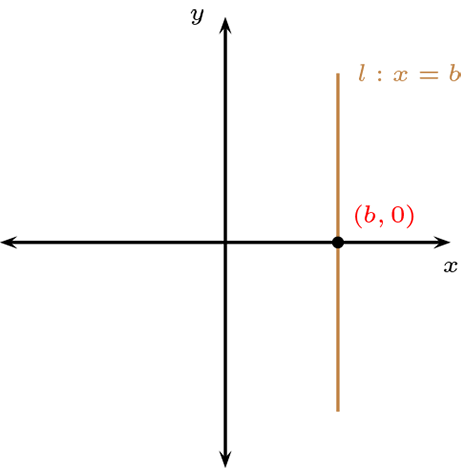
Y las rectas definida de la siguiente forma con \(\left ( m\lt 0\right )\)
\begin{equation*} l:y= \begin{cases} mx+b \amp ; x \geq 0 \\ \frac{m}{2}x+b \amp ; x\lt 0 \end{cases} \end{equation*}
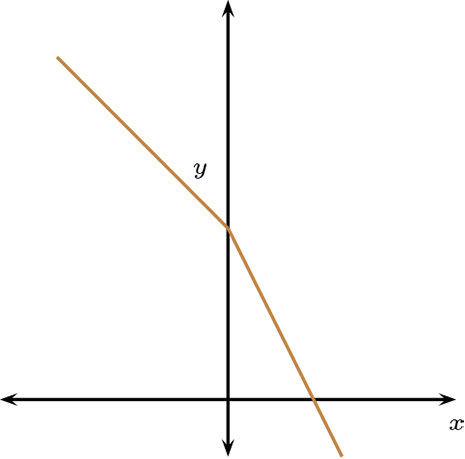
Por último la incidencia \(\mathcal{I}\) es la pertenecía.
Demostración
Tenga presente los siguientes ejemplos para la demostración.
Ejemplo 1.4.2
En el plano de Moulton.
Encuentra la ecuación de la recta que pasa por los puntos \((5,1)\) y \((7,4)\text{.}\)
Determinemos la pendiente de la recta que une estos dos puntos:
\begin{equation*}
m=\frac{y_2-y_1}{x_2-x_1}=\frac{4-1}{7-5}= \frac{3}{2}
\end{equation*}
Por lo tanto \(m\gt 0\) el cual implica que la recta es la habitual, es decir
\begin{equation*}
\frac{y-1}{x-5}= \frac{3}{2}
\end{equation*}
Despejando obtenemos
\begin{equation*}
y = \frac{3}{2}x- \frac{13}{2}
\end{equation*}
Subsección Ejercicios
En el plano de Moulton.
Determine la ecuación de la recta que pasa por los puntos \((1,0)\) y \((0,1).\)
Ejemplo 1.4.3
En el plano de Moulton.
Encuentra la ecuación de la recta que pasa por los puntos \((-2,5)\) y \((1,-2)\)
Determinemos la pendiente de la recta que une estos dos puntos:
\begin{equation*}
m=\frac{y_2-y_1}{x_2-x_1}=\frac{5+2}{-2-1}=- \frac{7}{3}
\end{equation*}
Por lo tanto \(m\lt 0\) el cual implica que debemos utilizar la definición de pendiente negativa, es decir,
\begin{equation*}
l:y= \begin{cases}
mx+b \amp ; x \geq 0 \\
\frac{m}{2}x+b \amp ; x\lt 0
\end{cases}
\end{equation*}
reemplazando los puntos \((-2,5),(1,-2)\) tenemos que
\begin{equation*}
\begin{array}{rcl|}
5 \amp = \amp -m+b \\
-2 \amp = \amp m+b \\ \hline
\end{array}
\end{equation*}
Sumando tenemos que \(3=2b\text{,}\) luego \(b=\frac{3}{2}\text{,}\) y restando tenemos que \(-7=2m\text{,}\) de lo cual \(m=-\frac{7}{2}\)
La recta pedida es:
\begin{equation*}
l:y= \begin{cases}
- \frac{7}{2}x+\frac{3}{2} \amp ; \amp x \geq 0 \\ \\
- \frac{7}{4}x +\frac{3}{2}\amp ; \amp x \lt 0
\end{cases}
\end{equation*}
Ejemplo 1.4.4
En el plano de Moulton. Dada la recta
\begin{equation*}
l:y= \begin{cases}
-2x+1 \amp ; \amp x \geq 0 \\ \\
-x+1 \amp ; \amp x \lt 0
\end{cases}
\end{equation*}
Encuentra la ecuación de la recta que pasa por los puntos \((2,5)\) y es paralela \(l\text{.}\)
La recta paralela debe estar dada por:
\begin{equation*}
l:y= \begin{cases}
-2x+b \amp ; \amp x \geq 0 \\ \\
-x+b \amp ; \amp x \lt 0
\end{cases}
\end{equation*}
y pasa por \((2,5)\text{,}\) luego \(-4+b=5\text{,}\) por ello \(b=9\text{.}\)
La recta pedida es:
\begin{equation*}
l:y= \left\{ \begin{array}{ccc}
-2x+9 \amp ; \amp x \geq 0 \\ \\
-x+9 \amp ; \amp x \lt 0
\end{array} \right.
\end{equation*}
Subsección Ejercicios
En el plano de Moulton.
Determinar tres puntos en cuadrantes distintos que no sean colineales.
Subsección Ejercicios
En el plano de Moulton considere los puntos
\begin{equation*}
A=(1,0), B =(0,1), C= (-2,1), D=( 1,-1).
\end{equation*}
Calcular \(l_{AB} \cap l_{CD}\)
Subsección Ejercicios
En el plano de Moulton considere los puntos
\begin{equation*}
A=(1,0), B = (-2,1), C=( 1,-1).
\end{equation*}
Determinar \(l_{C}\) tal que \(l_C\parallel l_{AB}\)
Subsección Ejercicios
En el plano de Moulton considere las rectas \(l_1, l_2\)
Determine condiciones que permitan decidir cuando \(l_1\) es paralela a \(l_2\text{.}\)