Sección 1.3 Haces de Paralelas
¶Ya que la relación de paralelismo es una relación de equivalencia en el plano afín, este se divide en clases de equivalencias llamadas cada clase un haz de paralelas, definidas por:
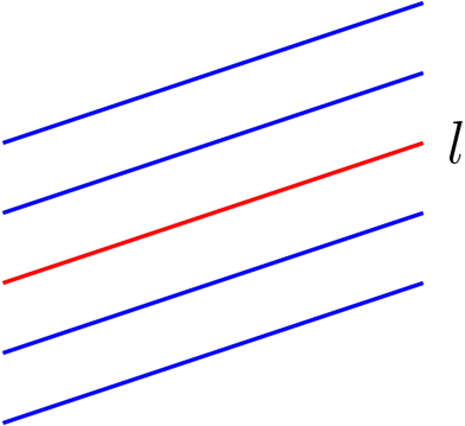
El plano afín minimal contiene tres haces de paralelas.
Por propiedad 1.1 y el ejemplo 1.1, sabemos que existen seis rectas las que definimos por \(l_1, \ l_2, \ l_3, \ l_4, \ l_5 \text{ y }l_6\) entonces veamos las rectas que son paralelas.
En la figura tenemos que

Teorema 1.3.2
El plano afín contiene al menos tres haces de paralelas.
Demostración
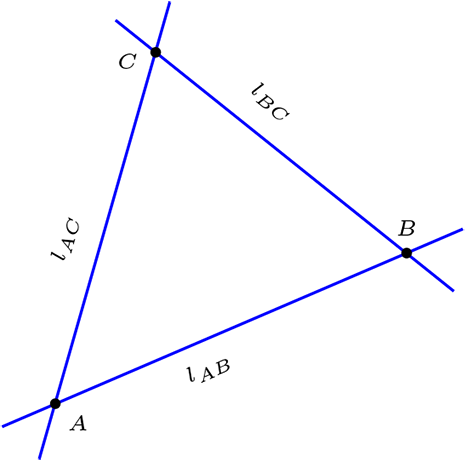
Por axioma tres existen \(A,B,C \in \mathcal{P}\) (tres puntos no colineales)
Por lo tanto \([l_{AC}] \neq [l_{AB}] \neq [l_{BC}]\neq [l_{AC}]\text{,}\) en consecuencia existen al menos tres haces de paralelas.
Teorema 1.3.3
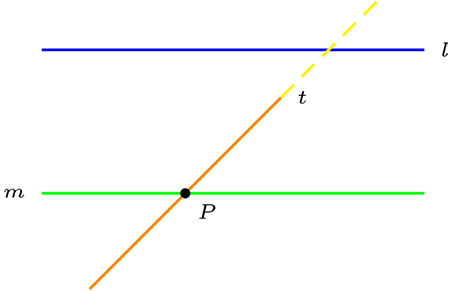
Sean \(\Pi\) plano afín, \(l,m,t \in \mathcal{L}\) tales que \(l \parallel m \text{ y } m \cap t =\{P\} \) entonces \(l \cap t \neq \varnothing\text{.}\)
Demostración
Por el absurdo, supongamos que \(l \parallel m\) y \(m \cap t \neq \varnothing \wedge l \cap t = \varnothing\text{,}\) es decir, \(l \parallel t\text{,}\) entonces \(l \parallel m,\ l \parallel t \text{ y } t \cap m =\{P\}\text{,}\) en consecuencia por \(P\) pasan dos rectas paralelas a \(l\text{,}\) lo cual es una contradicción por unicidad de axioma dos.
Teorema 1.3.4
Sea \(\Pi\) plano afín, entonces cada recta contiene el mismo número de puntos que inciden en ella.
Demostración
Dada \(l, m\in \mathcal{L}\text{,}\) denotamos por \(\mathcal{P}_l =\{P\in \mathcal{P}\ | \ P\mathcal{I}l\}\text{,}\) debemos probar que \(\#\mathcal{P}_l=\#\mathcal{P}_m\text{.}\)
La demostración se realizara en dos caso,
-
Supongamos que \(l \nparallel m \) entonces \(l \cap m = \{ P\}\)
Sea \(A \in \mathcal{P},\ A {\not\mathcal{I}} l \text{ y } A {\not\mathcal{I}} m\text{.}\) Por axioma dos sea \(l_{1} \in \mathcal{L}\) tal que \(A\mathcal{I}l_{1}\) y \(l_{1} \parallel l\text{,}\) de lo cual \(l_{1} \cap m=\{x_{1}\}\text{,}\) nuevamente por axioma dos tenemos que \(\exists! \ m_{1} \in \mathcal{L}\) tal que \(A\mathcal{I}m_{1} \text{ y } m_{1} \parallel m \text{,}\) luego \(m_{1} \cap l=\{x_{2}\}\text{.}\)
Gracias a estos antecedentes podemos construir la siguiente función:
\begin{equation*} \begin{matrix} f:\amp\{ x_2,P\} \amp \longrightarrow \amp \{ x_1,P \} \\ \amp x_{2} \amp\longrightarrow \amp x_{1} \\ \amp P \amp\longrightarrow \amp P \end{matrix} \end{equation*}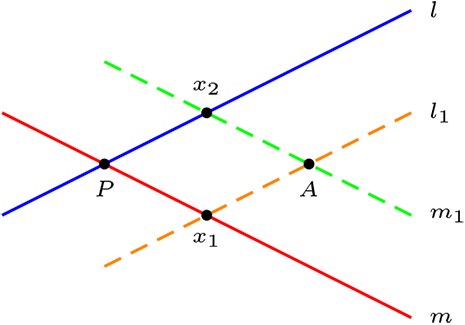
Ahora veamos otros puntos. Sea \(P_1 \ \mathcal{I} \ l \text{ tal que } P_1 \neq P \text{ y } P_1 \neq x_1 \text{.}\) Unimos \(P_1\) con \(A\) a través de la recta \(l_{A P_1}\text{,}\) entonces
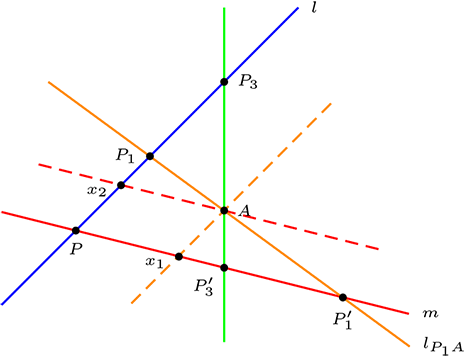
luego tenemos \(l_{A P_{1}} \nparallel m\text{,}\) es decir, \(l_{A P_{1}}\cap m \neq \phi\text{,}\) luego, \(l_{A P_{1}} \cap m = \{P'_{1}\}\text{.}\)
Por lo tanto
\begin{equation*} \begin{matrix} f: \amp\mathcal{P}_l\amp\longrightarrow \amp\mathcal{P}_m \\ \amp P_1\amp\longrightarrow\amp P'_{1}\\ \amp P\amp\longrightarrow \amp P \\ \amp x_2\amp \longrightarrow \amp x_1 \end{matrix} \end{equation*}De modo que \(f\) es una función biyectiva, entonces el \(\#\mathcal{P}_l =\#\mathcal{P}_m\)
-
Supongamos ahora que \(l \parallel m\text{.}\)
Sea \(t \in \mathcal{L}\) tal que \(t \cap l \neq \varnothing\text{,}\) por teorema anterior:
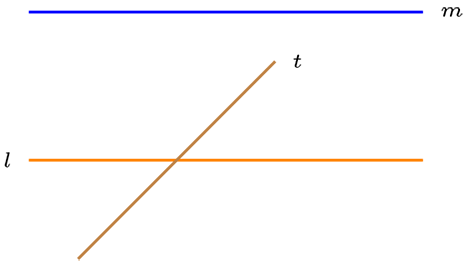
Sabemos que \(t \nparallel l \text{ y } t \nparallel m\) por la primera parte entonces
\begin{equation*} \#\mathcal{P}_t=\#\mathcal{P}_l \text{ y }\#\mathcal{P}_t=\#\mathcal{P}_m \end{equation*}del cual
\begin{equation*} \#\mathcal{P}_l=\#\mathcal{P}_m. \end{equation*}
Notación
Dada \(l\in \mathcal{L}\) y \(P\in \mathcal{P}\text{,}\) denotamos por
Definición 1.3.5
Se dice que el orden del plano \(\Pi\) es \(n\) si y sólo si cada recta contiene \(n\) puntos, y lo denotamos por \(\#\Pi=n\)
Ejemplo 1.3.6
\(\mathbb{Z}_{2} \times \mathbb{Z}_{2}\text{,}\) es un plano afín de orden dos.
\(\mathbb{R} \times \mathbb{R}\) es un plano afín de orden infinito.
Observación 1.3.7
Los planos afines finitos, conocidos hasta ahora, son de la forma \(\mathbb{F}_{q}\times \mathbb{F}_{q}\text{,}\) donde \(\mathbb{F}_{q}\) es un cuerpo finito con \(q\) elementos y \(q\) potencia de un primo.
Teorema 1.3.8
En un plano afín, todos los haces de rectas paralelas tienen la misma cantidad de rectas y esa cantidad es igual al orden del plano.
Demostración
Sean \(l,m \in \mathcal{L}\text{,}\) con \(l \cap m \neq \varnothing\) y \([l]\) haz de rectas paralelas de dirección \(l\text{.}\) Construimos la correspondencia de cada recta del haz, le asociamos la intersección con \(m\)
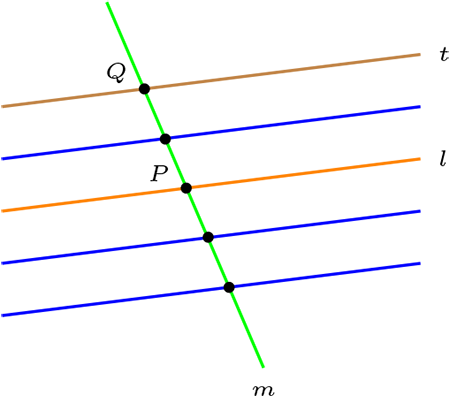
Por lo tanto \(\#[l]=\#\mathcal{P}_m\text{.}\) En consecuencia todas las haces de paralelas tienen la misma cantidad de rectas
Teorema 1.3.9
Sea \(\Pi\) un plano afín de orden \(n\text{,}\) entonces
Por un punto \(P\) pasan \(n+1\) rectas, \(\#\mathcal{L}_P = n+1\text{.}\)
El plano afín contiene \(n+1\) haces de paralelas.
El número de rectas en plano afín es \(n^2+n=\#\mathcal{L}\text{.}\)
La cantidad de puntos en el plano afín es \(n^2=\#\mathcal{P}\text{.}\)
Demostración
-
Sean \(P \in \mathcal{P}\text{ y } l \in \mathcal{L}\text{ tal que } P {\not\mathcal{I}} l\) en donde \(\#\Pi=n \wedge \#[l]=n\text{.}\)
Al unir cada punto de \(l\) con el punto \(P\) obtenemos \(n\)-rectas y por axioma dos
\begin{equation*} \left ( \exists!m\in \mathcal{L})(P\mathcal{I}m \wedge m \parallel l\right) \end{equation*}por lo tanto por \(P\) pasan \(n+1\) rectas.
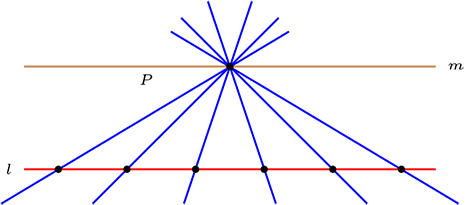
Dada un recta entonces existe una paralela que pasa por \(P\) y considerando el resultado anterior que por \(P\) pasan \(n+1\) rectas, entonces existen \(n+1\) haces de paralelas.
-
Sea \(l \in \mathcal{L}\text{,}\) luego pertenece a únicos haz de paralelas \([l]\text{,}\) cada haz tiene \(n\) rectas y por lo anterior hay \(n+1\) haces de paralelas, por lo tanto
\begin{equation*} \#\mathcal{L}=n(n+1)=n^2+n. \end{equation*}
-
Sea \([l]\) haz de paralelas, cada recta contiene \(n\) puntos y cada haz de paralelas contiene \(n\) rectas, por lo tanto
\begin{equation*} \#P=n\cdot n = n^2. \end{equation*}
Ejemplo 1.3.10
En el plano minimal tenemos que \(\# l =2\) entonces
Del cual se concluye que el plano minimal esta constituido de cuatro puntos y seis rectas.
