[skip-to-content]

Sección 4.3 Subespacio Afín

Para todo espacio afín, se define la nocíon de subespacio afín.

Definición 4.3.1

Sea \((V,X, \cdot)\) un espacio afín y \(\mathcal{U}\leq V\text{.}\) Se define

\begin{equation*} S(x_{0},\mathcal{U})=\left\{ \overrightarrow{u}\cdot x_{0} \ | \ \overrightarrow{u}\in \mathcal{U}\right\} \end{equation*}

en donde \(S(x_{0},\mathcal{U})\) se denomina subespacio afín, donde \(\mathcal{U}\) es la dirección del subespacio afín.

Sea \(V=X=\mathbb{R}^2\text{,}\) el Espacio Afín vectorial, luego

\begin{equation*} S\left( \left(1,10\right),\left\langle (1,4)\right\rangle\right) \end{equation*}

es un subespacio afín, con dirección \(\left\langle (1,4)\right\rangle\)

Notación

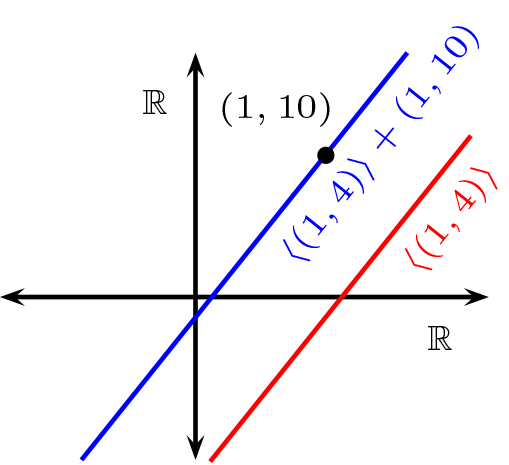
  1. Se dice que \(S(x_{0},\mathcal{U})\) es una recta afín si y sólo si \(\text{dim } \mathcal{U}=1\)

  2. Se dice que \(S(x_{0},\mathcal{U})\) es un plano afín si y sólo si \(\text{dim }\mathcal{U}=2\)

  3. Se dice que \(S(x_{0},\mathcal{U})\) es un hiperplano afín si y sólo si \(\text{dim }\mathcal{U}=\text{dim }V-1\)

  4. \(\text{dim }\left( S(x_{0},\mathcal{U})\right):=\text{ dim }\mathcal{U}\)

Sea \((V,X, \cdot)\) un espacio afín, y \(x\in X.\)

\begin{equation*} \begin{array}{cccc} t_x \amp V \amp\rightarrow \amp X \\ \amp \overrightarrow{v} \amp\mapsto\amp \overrightarrow{v} \cdot x \end{array} \end{equation*}

Es una función, ya que \(\overrightarrow{v} \cdot x\) es único. Además \(t_x(\overrightarrow{v})= t_x(\overrightarrow{w})\text{,}\) significa que \(\overrightarrow{v}\cdot x= \overrightarrow{w}\cdot x\text{,}\) pero es único, luego \(\overrightarrow{v}=\overrightarrow{w}\text{.}\)

Por último, dado \(y \in X\text{,}\) existe \(\overrightarrow{xy}\in V \) tal que \(t_x(\overrightarrow{xy})=y\text{.}\)

Por ello tenemos que

\begin{equation*} S(x, V)=X. \end{equation*}

En \(V=X=\mathbb{R}^4\) espacio afín evctorial. Sea \(\pi:2x+3y-4z+w=6\text{.}\)

Exprese \(\pi\) en términos de un subespacios afín.

Solución

Sea \((x,y,z,w)\in \pi\text{,}\) luego tenemos \(w=6-2x-3y+4z\text{,}\) reemplazando obtenemos,

\begin{equation*} \begin{array}{rcl} \amp\amp (x,y,z,w)\\ \amp = \amp (x,y,z,6-2x-3y+4z) \\ \amp = \amp (x,0,0,-2x)+(0,y,0,-3y)+(0,0,z,4z)+(0,0,0,6) \\ \amp = \amp x(1,0,0,-2)+y(0,1,0,-3)+z(0,0,1,4)+(0,0,0,6) \\ \end{array} \end{equation*}

Denotemos

\begin{equation*} x_0=(0,0,0,6),\ \ \ U=\left\langle (1,0,0,-2),(0,1,0,-3),(0,0,1,4) \right\rangle \end{equation*}

Luego

\begin{equation*} S\left(x_0,U \right)= (0,0,0,6)+\left\langle (1,0,0,-2),(0,1,0,-3),(0,0,1,4) \right\rangle \end{equation*}

Sean \((V,X,\cdot)\) un espacio afín y \(S(x_{0},\mathcal{U})\) un subespacio afín

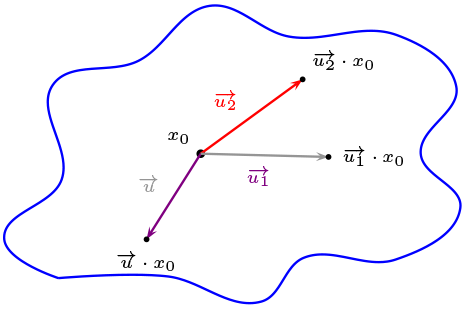
  1. Veamos primero \(\mathcal{U}\subseteq \left\{ \ \overrightarrow{xy} \ | \ x,y \in S(x_{0},\mathcal{U})\ \right\}\text{.}\)

    Sea \(\overrightarrow{u}\in \mathcal{U}\text{,}\) luego \(\overrightarrow{u}\cdot x_0, \ x_0 \in S(x_0,\mathcal{U})\) ya que \(\overrightarrow{u}\) y \(\overrightarrow{x_0 \left( \overrightarrow{u}\cdot x_0 \right) }\) envían \(x_0\) en \(\overrightarrow{u} \cdot {x_0}\) y la unicidad del vector tenemos

    \begin{equation*} \overrightarrow{x_0 \left( \overrightarrow{u}\cdot x_0 \right)}=\overrightarrow{u} \end{equation*}

    de este modo se tiene

    \begin{equation*} \mathcal{U}\subseteq \left\{\ \overrightarrow{xy} \ | \ x,y \in S(x_{0},\mathcal{U})\ \right\}. \end{equation*}

  2. Para la otra contención \(\left\{\ \overrightarrow{xy} \ | \ x,y \in S(x_{0},\mathcal{U})\ \right\}\subseteq \mathcal{U}\text{.}\)

    Sean \(x,y \in S(x_0,\mathcal{U})\text{,}\) por demostrar \(\overrightarrow{xy} \in \mathcal{U}\text{.}\)

    Como \(x,y \in S(x_0,\mathcal{U})\) se tiene que, existen \(\overrightarrow{u_1},\overrightarrow{u_2} \in \mathcal{U}\) tal que

    \begin{equation*} x = \overrightarrow{u_{1}}\cdot x_{0} \qquad \ y = \overrightarrow{u_{2}}\cdot x_{0} \end{equation*}

    Sea

    \begin{equation*} { \begin{array}{ccrclr} \amp\amp \overrightarrow{xy} \amp = \amp \overrightarrow{w} \\ \amp\amp \overrightarrow{ \left( \overrightarrow{u_{1}}\cdot x_{0}\right) \left( \overrightarrow{u_{2}}\cdot x_{0}\right)} \amp = \amp \overrightarrow{w} \amp / \cdot \overrightarrow{u_{1}}\cdot x_{0} \\ \amp \amp \overrightarrow{ \left( \overrightarrow{u_{1}}\cdot x_{0}\right) \left( \overrightarrow{u_{2}}\cdot x_{0}\right)}\cdot \overrightarrow{u_{1}}\cdot x_{0} \amp = \amp \overrightarrow{w}\cdot \left(\overrightarrow{u_{1}}\cdot x_{0} \right)\amp \\ \amp \amp \overrightarrow{u_{2}}\cdot x_{0} \amp = \amp \left( \overrightarrow{w}+ \overrightarrow{u_{1}}\right) \cdot x_{0} \amp /-\overrightarrow{u_{2}}\cdot \\ \amp \amp x_{0} \amp = \amp \left( -\overrightarrow{u_{2}}+\overrightarrow{w}+\overrightarrow{u_{1}}\right) \cdot x_{0} \amp \\ \end{array}} \end{equation*}

    Por unicidad

    \begin{equation*} \begin{array}{rcl} -\overrightarrow{u_2}+\overrightarrow{w}+\overrightarrow{u_1} \amp = \amp \overrightarrow{0} \\ \overrightarrow{w} \amp = \amp \overrightarrow{u_2}-\overrightarrow{u_1} \end{array} \end{equation*}

    con \(\overrightarrow{u_2}-\overrightarrow{u_1} \in \mathcal{U}\text{,}\) luego \(\overrightarrow{w} \in \mathcal{U}\text{.}\)

Sean \((V,X, \cdot)\) un espacio afín, \(x,z \in X,\ \mathcal{U} \leq V\text{,}\) y \(z \in S(x,\mathcal{U})\) luego tenemos que \(z= \overrightarrow{u}\cdot x\) , con \(\overrightarrow{u}\in \mathcal{U}\)

Ahora bien, notemos que

\begin{equation*} \overrightarrow{w}\cdot z= \overrightarrow{w}\cdot (\overrightarrow{u}\cdot x) = (\overrightarrow{w}+\overrightarrow{u})\cdot x \end{equation*}

por ello \(S(z, \mathcal{U})\subseteq S(x, U\mathcal{})\text{.}\)

análogamente, obtenemos que

\begin{equation*} (-\overrightarrow{u})\cdot z= (-\overrightarrow{u})\cdot(\overrightarrow{u}\cdot x)= (-\overrightarrow{u}+\overrightarrow{u})\cdot x =x \end{equation*}

y con ello la otra contención.

\begin{equation*} S(x, \mathcal{U})= S(z, \mathcal{U}). \end{equation*}

De \(S(x, \mathcal{U})= S(z, \mathcal{U})\text{,}\) tenemos que \(x\in S(z, \mathcal{U})\text{,}\) luego existe \(\overrightarrow{u}\in \mathcal{U}\) que cumple con

\begin{equation*} \overrightarrow{u}\cdot z= x= \overrightarrow{xz}\cdot x \end{equation*}

es decir, \(\overrightarrow{xz}=\overrightarrow{u}\in \mathcal{U}\text{.}\)

Sea \(z \in S(x,\mathcal{U}) \cap S(w,\mathcal{W})\) , luego por la propiedad anterior tenemos que

\begin{equation*} S(x,\mathcal{U})=S(z,\mathcal{U})\ \ \wedge \ \ S(w,\mathcal{W})=S(z,\mathcal{W}) \end{equation*}

Ahora demostraremos que

\begin{equation*} S(z,\mathcal{U})\cap S(z,\mathcal{W})= S(z,\mathcal{U}\cap\mathcal{W}) \end{equation*}

Para ello, sea \(u \in S(z,\mathcal{U})\cap S(z,\mathcal{W})\text{,}\) luego tenemos por teorema anterior

\begin{equation*} \overrightarrow{uz} \in \mathcal{U}\ \wedge \ \overrightarrow{uz} \in \mathcal{W}, \end{equation*}

de lo cual tenemos \(\overrightarrow{uz} \in \mathcal{U}\cap \mathcal{W}\text{,}\) de este modo \(u \in S(z,\mathcal{U}\cap\mathcal{W})\text{.}\)

Para la otra contención, sea \(u \in S(z,\mathcal{U}\cap \mathcal{W})\text{,}\) luego tenemos por teorema anterior \(\overrightarrow{uz} \in \mathcal{U}\cap \mathcal{W}, \) de lo cual tenemos \(\overrightarrow{uz} \in \mathcal{U} \wedge \overrightarrow{uz}\in \mathcal{W}\text{,}\) de este modo \(u \in S(z,\mathcal{U}) \cap S(z,\mathcal{W})\text{.}\)

Supongamos que \(\mathcal{U}=\mathcal{W}\) y \(S(x,\mathcal{U})\cap S(w,\mathcal{W})\neq \varnothing\text{,}\) por demostrar que \(S(x,\mathcal{U})=S(w,\mathcal{W})\text{.}\)

Sea \(z \in S(x,\mathcal{U})\cap S(w,\mathcal{U})\text{,}\)

\begin{equation*} S(x,\mathcal{U})=S(z,\mathcal{U})=S(z,\mathcal{W})= S(w,\mathcal{W}) \end{equation*}

Ahora supongamos que \(S(x,\mathcal{U})=S(w,\mathcal{W})\text{,}\) por demostrar \(\ \mathcal{U}=\mathcal{W} \) y \(S(x,\mathcal{U})\cap S(w,\mathcal{W})\neq \varnothing\)

Por teorema anterior

\begin{equation*} \begin{array}{rcl} \mathcal{U} \amp = \amp \left\{ \overrightarrow{zu} \in V \ | \ z,u \in S(x,\mathcal{U}) \right\} \\ \amp = \amp \left\{ \overrightarrow{zu} \in V \ | \ z, u \in S(w, \mathcal{W}) \right\} \\ \amp = \amp \mathcal{W} \end{array} \end{equation*}

Además \(S(x, \mathcal{U})=S(w,\mathcal{W})\text{,}\) se tiene entonces que \(S(x,\mathcal{U}) \cap S(w,\mathcal{W}) \neq \varnothing\text{.}\)

Grupo de las Traslaciones.

Sea \((V,X,\cdot)\) un espacio afín y \(\overrightarrow{u} \in V\)

\begin{equation*} \begin{array}{cccl} t_{\overrightarrow{u}}: \amp X \amp \rightarrow \amp X \\ \amp x \amp \rightsquigarrow \amp t_{\overrightarrow{u}}(x)=\overrightarrow{u}\cdot x \end{array} \end{equation*}

Se dice que \(t_{\overrightarrow{u}}\) es una traslación en la dirección del vector \(\overrightarrow{u}\text{,}\) en el conjunto \(X\text{.}\)

  1. \(t_{\overrightarrow{u}}\) es inyectiva, sean \(x, y \in X\) por demostrar \(t_{\overrightarrow{u}}(x)=t_{\overrightarrow{u}}(y)\text{,}\) entonces \(x=y\)

    Para ello veamos

    \begin{equation*} \begin{array}{rcl} t_{\overrightarrow{u}}(x)\amp = \amp t_{\overrightarrow{u}}(y) \\ \overrightarrow{u}\cdot x \amp = \amp \overrightarrow{u}\cdot y \\ -\overrightarrow{u}\cdot \left(\overrightarrow{u}\cdot x \right) \amp = \amp -\overrightarrow{u}\cdot \left( \overrightarrow{u}\cdot y \right) \\ \overrightarrow{0}\cdot x \amp = \amp \overrightarrow{0} \cdot y \\ x \amp = \amp y \end{array} \end{equation*}

    De este modo \(t_{\overrightarrow{u}}\text{ es inyectiva}\text{.}\)

  2. \(t_{\overrightarrow{u}}\) es epiyectiva, por demostrar que \(\text{Rec } (t_{\overrightarrow{u}})=X\)

    La primera contención es evidente que \(\text{Rec } (t_{\overrightarrow{u}})\subseteq X\text{,}\) basta demostrar que \(\text{Rec } (t_{\overrightarrow{u}})\supseteq X\text{.}\)

    Dado \(x \in X\)

    \begin{equation*} \begin{array}{rcl} t_{\overrightarrow{u}}\left( -\overrightarrow{u} \cdot x \right) \amp = \amp \overrightarrow{u}\left( -\overrightarrow{u}\cdot x \right) \\ \amp = \amp \left( \overrightarrow{u}+(-\overrightarrow{u} \right) )\cdot x \\ \amp = \amp \overrightarrow{0}\cdot x \\ \amp = \amp x \end{array} \end{equation*}

Luego \(t_{\overrightarrow{u}}\) es epiyectiva, de este modo \(t_{\overrightarrow{u}}\) es biyectiva.

Notación
\begin{equation*} \mathcal{T}(X)=\left\{t_{\overrightarrow{u}} \ | \ \overrightarrow{u} \in V\right\} \end{equation*}

Consideremos las aplicación, que además cumple con:

\begin{equation*} \begin{array}{rcl} \mathcal{T}(X) \amp \cong \amp (V,+) \\ t_{\overrightarrow{u}} \amp \leftrightarrow \amp \overrightarrow{u} \\ t_{\overrightarrow{u}}^{-1} \amp \leftrightarrow \amp -\overrightarrow{u} \\ t_{\overrightarrow{u}} \circ t_{\overrightarrow{v}} \amp \leftrightarrow \amp t_{\overrightarrow{u}+\overrightarrow{v}} \end{array} \end{equation*}

Además por unicidad tenemos \(t_{\overrightarrow{u}}(x)=t_{\overrightarrow{v}}(x)\) se tiene que \(\overrightarrow{u}= \overrightarrow{v}\text{.}\)

Sean \(\overrightarrow{u},\overrightarrow{v}\in V\) y \(x_0\in X\)

\begin{equation*} \begin{array}{rcl} t_{\overrightarrow{v}}(S(x_0, \lt \overrightarrow{u}\gt ) \amp=\amp t_{\overrightarrow{v}}\left(\left\{ \alpha\overrightarrow{u}\cdot x_{0} \ | \ \alpha \in \mathbb{K} \right\} \right) \\ \amp=\amp\left\{ t_{\overrightarrow{v}}(\alpha\overrightarrow{u}\cdot x_{0}) \ | \ \alpha\in \mathbb{K}\right\} \\ \amp=\amp\left\{ \overrightarrow{v}\cdot (\alpha\overrightarrow{u}\cdot x_{0}) \ | \ \alpha\in \mathbb{K}\right\} \\ \amp=\amp\left\{\alpha \overrightarrow{u}\cdot (\overrightarrow{v}\cdot x_{0}) \ | \ \alpha\in \mathbb{K}\right\} \\ \amp=\amp (S( \overrightarrow{v}\cdot x_0, \lt \overrightarrow{u}\gt ) \end{array} \end{equation*}