Proposición 3.4.1
El plano \(\Pi=(\mathcal{L},\ \mathcal{P},\ \mathcal{I}, \ \perp)\text{,}\) es un Plano Elíptico.
En esta seccion estudiaremos los planos métricos, que no cumplen el quinto axioma de Euclides, una de las posible forma es la no existencia de rectas paralelas, a continuacion construiremos modelos de la realización de estos planos Elípticos
Un plano elíptico \(\Pi=(\mathcal{L},\ \mathcal{P},\ \mathcal{I}, \ \perp)\) es un plano métrico \(\Pi\) que satisface el axioma elíptico, es decir,
Los axiomas afines
Los axiomas de ortogonalidad
Los axiomas de colinealidad
Axioma elíptico: Para toda \(l,m \in \mathcal{L} \text{, entonces } l \cap m \neq \varnothing\)
Construyamos un modelo de Plano Elíptico, para ello consideremos la esfera unitaria y centro en el origen, es decir,
Notemos que una recta vectorial intersecta a la esfera \(S \) en dos puntos.
Puntos del plano elíptico
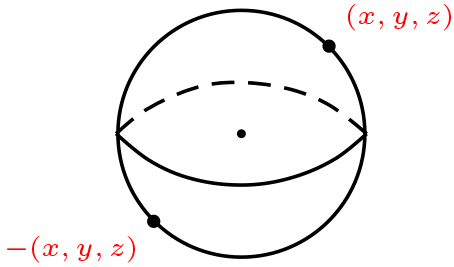
Los puntos \([(x,y,z),(-x,-y,-z)]\) se les llama puntos antipolares o bipuntos, tambien por comodidad lo denotamos por \([(x,y,z),(-x,-y,-z)]=\lt (x,y,z)\gt \)
Un plano vectorial intersecta a la esfera \(S\) en una circunferencia de radio máximo.
Rectas del plano elíptico
\(\mathcal{L}=\{\text{circunferencia de radio máximo de }S\}\text{,}\) si \(l_1,l_2\) son rectas, entonces en \(S\) tienen ecuaciones de la forma:
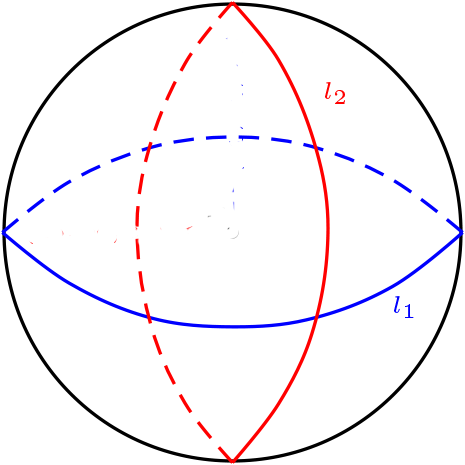
La incidencia\(P \mathcal{I} l\) si y sólo si \(P\subseteq l\)
La Ortogonalidad en \(\mathcal{L}\text{.}\)
Sean \(l_1\) y \(l_2\) en \(\mathcal{L}\text{,}\) definida por:
note que podemos escribir las ecuaciones del siguiente modo
Los vectores \((a_1, b_1, c_1),(a_2, b_2, c_2)\) son perpendicular a los respectivos planos en el espacio.
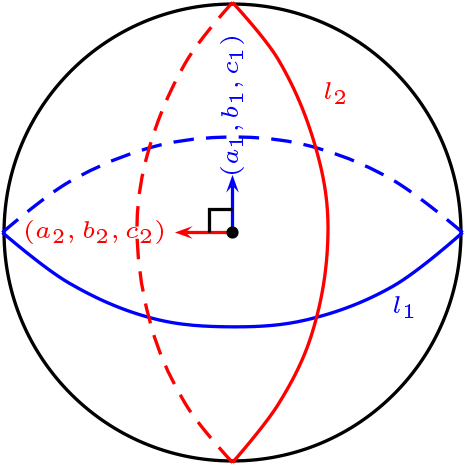
Por ello se define, la ortogonalidad
El plano \(\Pi=(\mathcal{L},\ \mathcal{P},\ \mathcal{I}, \ \perp)\text{,}\) es un Plano Elíptico.
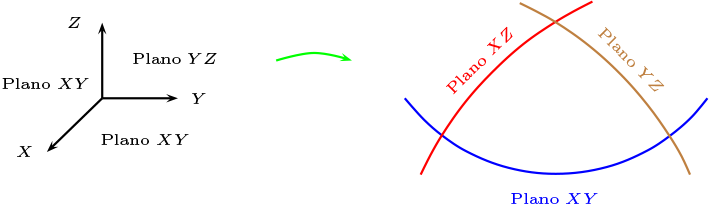
Consideremos las planos \(XY\text{,}\)\(XZ\) y \(YZ\) donde las ecuaciones están dadas por \(l_z: z=0\text{,}\) \(l_y: y=0\text{,}\) \(l_x :x=0\) respectivamente.
Los rectas en el plano elíptico son perpendiculares ya que
Una visualización en el primer octante \(x,y,z>0\text{,}\) de los planos asociado a los ejes están dados por
Sean \(\Pi\) plano métrico y \(a,b,c \in \mathcal{L}\text{.}\)
Se dice que \(a,b,c\) es un Triángulo Polar si y sólo si \(a \perp b , \ b \perp c \) y \(c \perp a\text{.}\)
En el figura anterior, tenemos que \(x=0\text{,}\) \(y=0\text{,}\) \(z=0\) forman un triángulo polar en el primer octante, con los bipuntos \(\lt (1,0,0)\gt, \lt (0,1,0)\gt, \lt (0,0,1)\gt\) y además la suma de los ángulos interiores de este triángulo son tres rectos.
Sea \(\Pi\) plano métrico, \(P \in \mathcal{P}\) y \(l \in \mathcal{L}\text{.}\)
Se dice que \(P\) es polo de \(l\) si y sólo si existen \(u,v \in \mathcal{L}\text{,}\) distintas tales que \(u \perp l , \ v \perp l\) y \(u \cap v = \{ P \}\text{.}\)
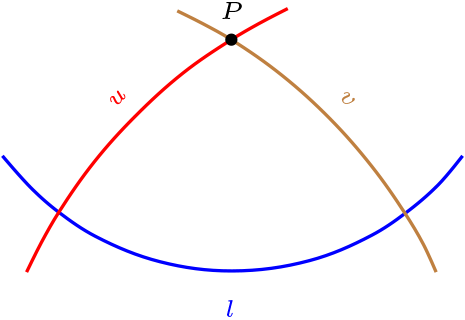
Comprobar que \(\lt (0,0,1)\gt\) es el polo de \(l=\lt (0,1,0), (1,0,0)\gt\text{.}\)
En la figura anterior, tenemos que \(u=\lt (1,0,0), (0,0,1)\gt\text{,}\) \(v=\lt (0,1,0), (0,0,1)\gt\) son recta ortogonales a \(l\text{,}\) ya que forman un triángulo polar.
Sea \(\mathbb{P}_{2}(\mathbb{R}^3)\) plano elíptico.
Determinar la recta que une \(P=\left\langle (2,3,-1)\right\rangle\) y \(Q=\left\langle(1,1,5)\right\rangle\)
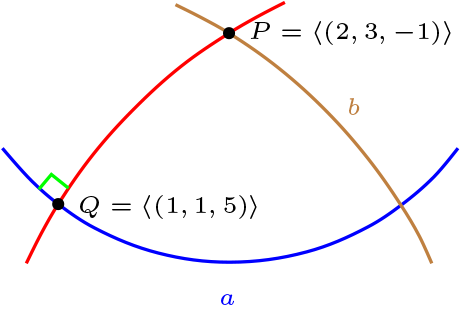
La recta que pasa por \(P\) y \(Q\) es
y su ecuación cartesiana esta dada por
De lo cual se obtiene \(l_{PQ}:16x-11y-z=0\text{.}\)
Además note que las rectas
son perpendiculars \(l_{PQ}\) ya que
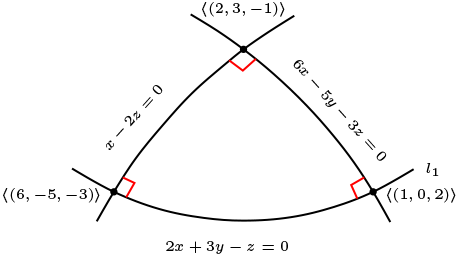
Sean \(\mathbb{P}_{2}(\mathbb{R}^3)\) plano elíptico, \(l:2x+3y-z=0\) y \(\delta = \left \langle (1,0,2) \right \rangle\text{.}\)
Determinar los lados y vértices del triángulo polar formado por el vértice \(\delta \) y el lado \(l\text{.}\)
Teniendo presente el ejemplo anterior tenemos que la recta que une los puntos
Luego
Todo plano vectorial en \(\mathbb{R}^3\) es el eje de una simetría
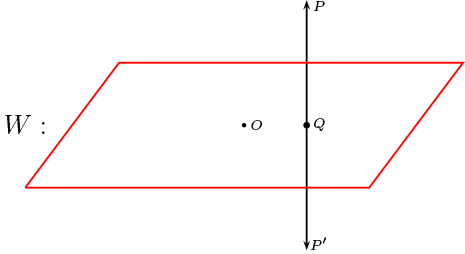
Los puntos \(P,P'\) son simétricos respecto al plano.
Teniendo presente el producto interno usual en \(\mathbb{R}^3\text{,}\) obtenemos un resultado similar, esto es
donde \(\overrightarrow{n}\) es perpendicular al plano \(W\text{.}\)
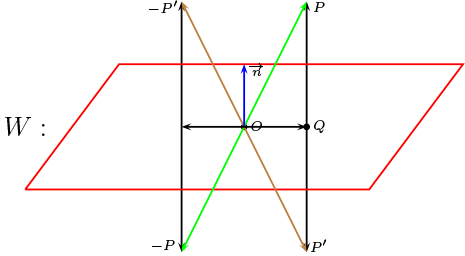
Si \(d(O,P)= d(O,P')= d(0,-P)=d(O,-P')\text{,}\) luego si uno de ello pertenece a la circunferencia unitaria, todos pertenecen, por ello tenemos la definida la simetría en los puntos antipolares de Plano Elíptico del siguiente modo
Sea \(\Pi\) el modelo de plano elíptico sobre la esfera, y la recta \(l: ax+by+cy=0\text{,}\) entonces la simetría asociada a \(l\) esta dada por
donde \(\overrightarrow{n}=(a,b,c)\text{.}\)
Sea \(\mathbb{P}_{2}(\mathbb{R}^3)\) plano elíptico.
Determinar la simetrías en el plano elíptico respecto a la recta
En \(\mathbb{R}^3\text{,}\) notemos que \(\overrightarrow{n}= (2,3,-1)\) y \(\overrightarrow{n}\cdot overrightarrow{n}= 4+9+1=14\text{,}\) con lo anterior tenemos la simetría esta dada por
aplicada a un punto antipolar o bipunto, como por ejemplo tenemos
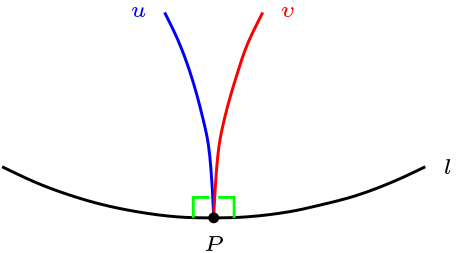
Sea \(\Pi\) plano métrico y \(P\) polo de \(l\text{,}\) entonces \(P \not\mathcal{I} l\)
Supongamos que \(P \mathcal{I} l\text{.}\)
Por \(P\) pasan dos rectas perpendiculares a \(l\text{,}\) y estas son \(u,v\) esto es una contradicción, ya que por la recta \(l\) solo pasa una recta perpendicular en \(P\text{.}\)
Sea \(\Pi\) plano métrico.
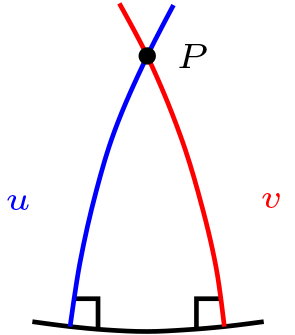
Si \(P\) es polo de \(l\text{,}\) entonces \(R_l(P)=P\)
Si \(P\) es un polo de \(l\text{,}\) luego existen \(u,v \in \mathcal{L}\text{,}\) con \(u \neq v\text{,}\) tales que \(u \perp l, \ v \perp l \) y \(u \cap v= \{P\}\text{.}\)
Por propiedad anterior tenemos que
de este modo tenemos que
es decir \(R_{l}(P)=P\text{.}\)
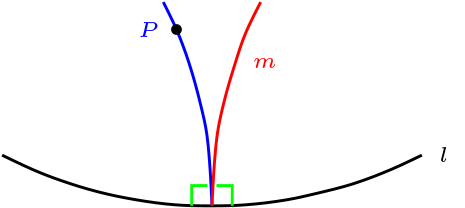
Sea \(\Pi\) plano métrico.
Si \(P\) es polo de \(l\) y \(m \perp l \text{,}\) entonces \(P \mathcal{I} m\)
Supongamos que \(l \cap m = \{ Q \}\text{,}\) entonces \(R_{l}(Q)=Q\text{.}\)
Dada la recta \(l_{PQ}\text{,}\) pero \(P\) y \(Q\) son fijos por \(R_l\text{,}\) entonces \(R_{l}(l_{PQ})=l_{PQ}\) por eso es perpendicular a la recta \(l\text{.}\)
Luego tenemos
Sea \(\Pi\) un plano métrico, entonces cada recta tiene a lo mas un polo.
Supongamos que \(P_1\) y \(P_2\) son polo de \(l\text{,}\) si \(P_1\) es polo de \(l\text{,}\) entonces \(\exists \ u,v \in \mathcal{L}\) distintas tales
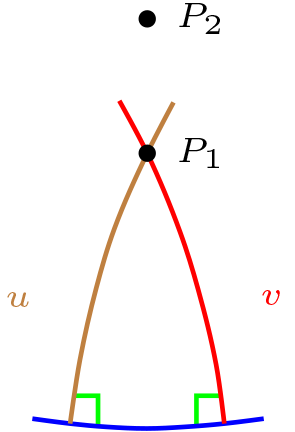
Pero \(u \perp l \) y \(v \perp l\text{,}\) por teorema anterior \(P_2 \mathcal{I}u\) y \(P_2 \mathcal{I}v\text{,}\) si los puntos fueran distintos las recta \(u,v\) serían iguales lo cual es imposible, por lo tanto \(P_1=P_2\text{,}\) es decir
Sea \(\Pi\) plano métrico.
Si \(P\) es polo de \(l\) y \(P \mathcal{I}m\text{,}\) entonces \(l \perp m\text{.}\)
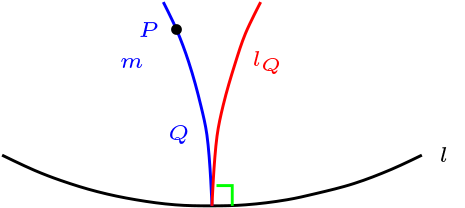
Sea \(Q \mathcal{I}m\text{,}\) tal que \(Q\neq P\) y sea \(l_Q \in \mathcal{L}\) tal que \(Q \mathcal{I}l_Q \ \wedge \ l_Q \perp l\text{,}\) por ello tenemos que \(P \mathcal{I}l_Q \) y además \(Q, P \mathcal{I}m\text{,}\) por ello
Sea \(\Pi\) plano métrico.
Si \(P\) es polo de \(l\text{,}\) entonces todo punto tiene un recta polar y toda recta tiene un polo.
Sea \(\Pi\) plano métrico y \(P\) es polo de \(l\text{.}\) Dado \(Q\) un punto en el plano métrico.
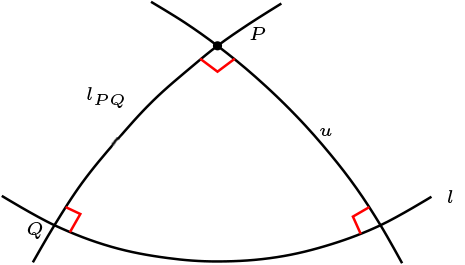
Primer caso \(Q\mathcal{I}l\text{.}\)
Sea \(l_{PQ}\) la recta que une \(P\text{,}\) \(Q\text{,}\) además \(u\) recta ortogonal a \(l_{PQ}\) en el punto \(P\text{,}\) por ello tenemos que
Además ambas contiene a \(Q\text{.}\)
Segundo caso \(Q\not\mathcal{I} l\text{.}\)
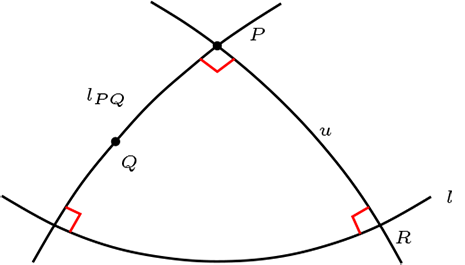
Sea \(l_{PQ}\) la recta que une \(P\text{,}\) \(Q\text{,}\) de este modo tenemos \(l_{PQ} \perp l\text{.}\) Además sea \(u\) la recta tal que \(u\perp l_{PQ}\) y contiene \(P\text{,}\) de este modo \(l_{PQ}\) es la recta polar de \(u \cap l=\{R\}\) y \(Q\) pertenece a ella. Aplicando el caso anterior, se construye la recta polar.
Para la otra parte.
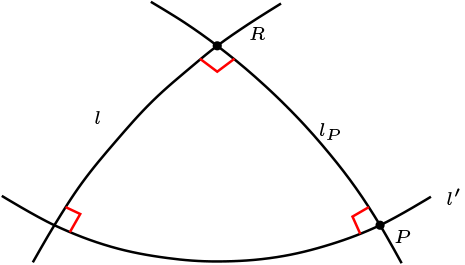
Dado \(l'\) una recta, luego contiene un punto \(P\) y por lo anterior el tiene una recta polar \(l\text{.}\) Luego tenemos \(l\perp l'\text{.}\) Consideremos \(l_P\text{,}\) la recta perpendicular a \(l'\) en el punto \(P\text{,}\) por ello \(l_P \perp l\text{,}\) de este modo tenemos que \(l_P \cap l =\{R\}\) es el polo de \(l'\text{.}\)
Sea \(\Pi\) plano elíptico.
Si \(P\) es polo de \(l\text{,}\) entonces \(P\) tiene solamente una recta polar.
Sea \(P\) polo de \(l\) y \(l'\text{.}\)
Toda recta ortogonal a \(l\text{,}\) pasa por \(P\text{,}\) y por ende es ortogonal a \(l'\) y toda recta \(l''\) tal que \(P \mathcal{I}l''\) tenemos que \(l'' \perp l \) y \(l'' \perp l'\text{.}\)
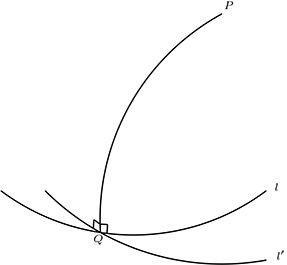
Sea \(Q \mathcal{I}l \ \wedge \ Q \mathcal{I}l'\text{,}\) \(l_Q\) la recta ortogonal a \(l\text{,}\) luego \(P \mathcal{I}l_Q\text{,}\) de lo cual \(l_Q \perp l'\text{.}\)
Es decir, \(l,l'\) son ortogonales a \(l_Q\) en el punto \(Q\text{,}\) luego por unicidad de la recta ortogonal, tenemos que \(l=l'\text{.}\)
Sea \(\Pi\) plano métrico.
Si cada recta contiene un polo, entonces \(\Pi\) es un plano elíptico.
Sea \(l_{1},l_{2} \in \mathcal{L}\text{,}\) por demostrar que \(l_{1} \cap l_{2} \neq \varnothing\text{.}\)
Supongamos que \(P\) es el polo de \(l_1\) y \(Q\) es polo de \(l_{2}\text{,}\) como \(l_{1},l_{2} \perp l_{PQ}\text{,}\) entonces \(l_{1}\) y \(l_{2}\) pasan por el polo de \(l_{PQ}\text{,}\) por lo tanto
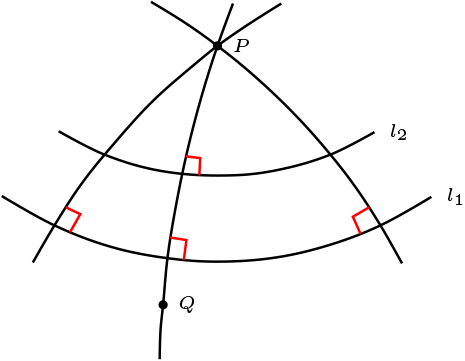
Las siguientes proposiciones son equivalentes:
\(\Pi\) es un plano elíptico.
Cada recta tiene un polo.
Cada punto tiene una recta polar.
Existe un par polo-polar.
El plano \(\Pi\) contiene un triángulo polar.
Sea \(\Pi\) un plano elíptico, por demostrar que cada recta tiene un polo.
Dada la recta \(l\) y \(A,B \mathcal{I}l\text{.}\)
Sean \(u,v \in \mathcal{L}\text{,}\) tal que \(A\mathcal{I}u\text{,}\) \(u \perp l\) y \(B\mathcal{I}v \text{,}\) \(v\perp l\text{,}\) de este modo tenemos \(u\cap v=\{P\}\text{,}\) de donde \(P\) es el polo de \(l\text{.}\)
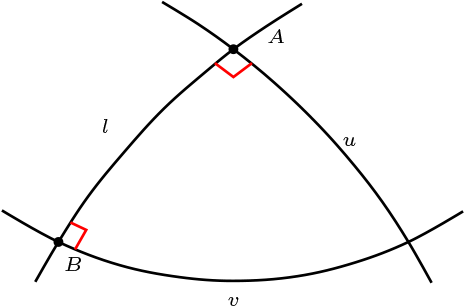
Si cada recta tiene un polo, por demostrar cada punto tiene una polar.
Sea \(P\) un punto, escogemos \(Q\) otro punto, luego la recta \(l_{PQ}\) tiene un polo \(R\text{,}\) trazamos la recta \(l_{PR}\) y la recta ortogonal a \(l_R\text{,}\) ortogonal a \(l_{PR}\text{,}\) de la construcción obtenemos que \(l_R\) es la recta polar a \(P\text{.}\)
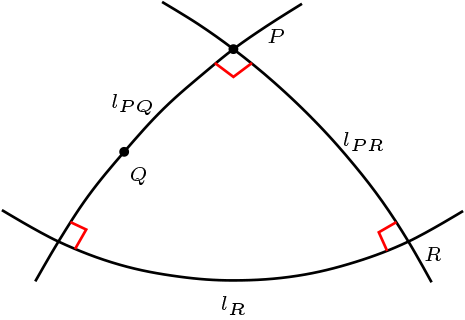
Si cada punto tiene una recta polar entonces existe un par polo-polar.
Este demostración se deja para el lector, dado que es trivial.
Si existe un par polo-polar entonces el plano \(\Pi\) contiene un triángulo polar.
Sea \((P,l)\) par polo polar.
Sea \(m \in \mathcal{L}\) tal que \(m \perp u \ \wedge P \mathcal{I} m\text{,}\) entonces \(m \perp l\)
existe un triángulo polar.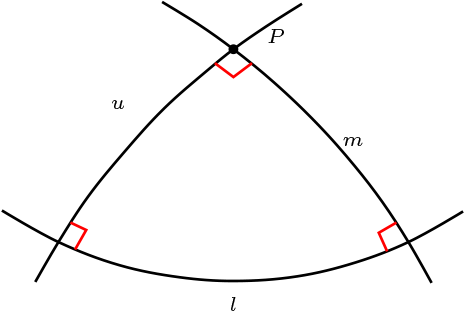
Si existe un triángulo polar entonces \(\Pi\) es un plano elíptico.
Sea \((P,l)\) una par polar, por teorema \ref{teo33} toda recta tiene un polo y aplicando teorema \ref{teo35} \(\Pi\) es elíptico.
Sean \(\Pi\) plano elíptico y \((P,l)\) par polo-polar.

Si \(P\) es polo de \(l\text{,}\) entonces existen \(u,v \in \mathcal{L}\) tales que \(u,v \perp l \text{ } \wedge \text{ } u \cap v = \{P\}\text{.}\)
De lo cual obtenemos que \(R_{l}(P) = P\text{.}\)
Recordemos que una rotación \(\sigma\) de centro \(Q\) en un plano métrico significa que existen \(u,v \in \mathcal{L}\) tales que \(u\cap v =\{Q\}\) y \(\sigma = R_u\circ R_v\)
Sea \(\Pi\) plano elíptico y \(\sigma\) una rotación de centro \(P\text{,}\) entonces existe \(l \in \mathcal{L}\) tal que \(\sigma(l)=l \ \wedge \ P \not\mathcal{I} l\text{.}\)
Sea \(\sigma\) es rotación, entonces
Sea \(t\) la recta polar de \(P\text{,}\) de donde se tiene que \(m \perp t \ \wedge \ l \perp t\text{,}\) entonces
De este modo se obtiene que \(t\) esta fija.

Sea \(\Pi\) plano elíptico y \(H_P\) una simetría puntual, entonces \(H_P\) fija tres puntos.
Como \(H_P\) es una simetría puntual, existen \(u,v \in \mathcal{L}\) tales que \(u\cap v =\{P\} \wedge u\perp v\) y \(H_P = R_u\circ R_v\text{.}\)
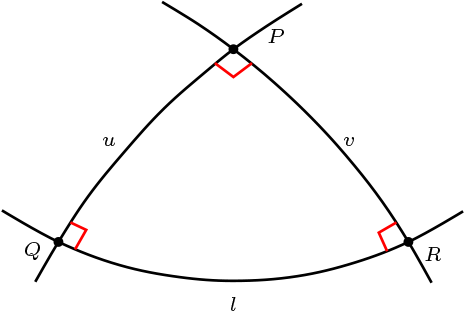
Sea \(l\) la recta polar de \(P\text{,}\) y los puntos de incidencia \(l\cap u=\{Q\}\wedge l\cap v=\{R\}\text{.}\) Por propiedad anterior \(H_P(l)=l\text{.}\)
Sabemos que \(Q\mathcal{I}l,u\text{,}\) \(R_v(Q)\mathcal{I}l, u\text{,}\) de lo cual tenemos \(R_v(Q)=Q\) y por ende tenemos \(H_P(Q)=Q\) análogamente \(H_P(R)=R\text{.}\)