Sección 1.2 Axioma del plano afín
¶Un estructura de incidencia \(\Pi=(\mathcal{P},\mathcal{L},\mathcal{I})\text{,}\) se dice que \(\Pi\) es un plano afín si y sólo si cumple los siguientes axiomas
-
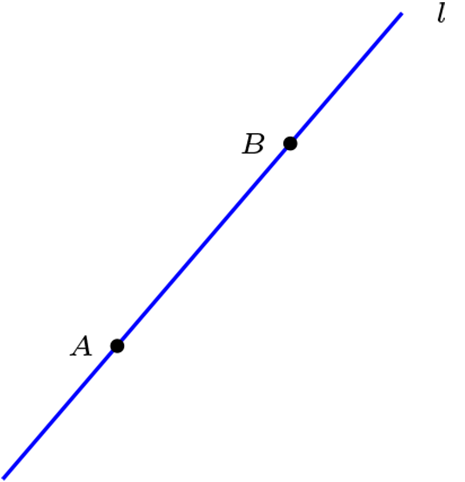
Sean \(A,B \in \mathcal{P}\text{,}\) \(A \neq B \text{ entonces } \exists ! \ l \in \mathcal{L}\) tal que \(A \mathcal{I}l \text{ y } B \mathcal{I}l\)
La única recta se denota por \(l_{AB}\text{.}\)
-
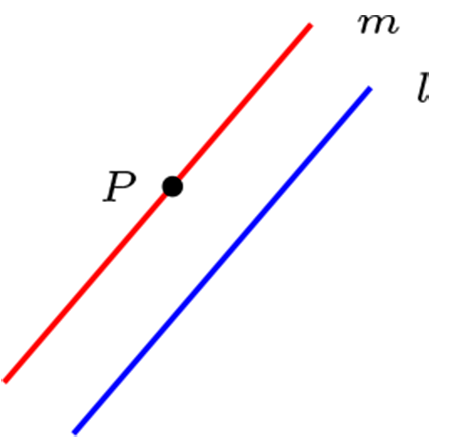
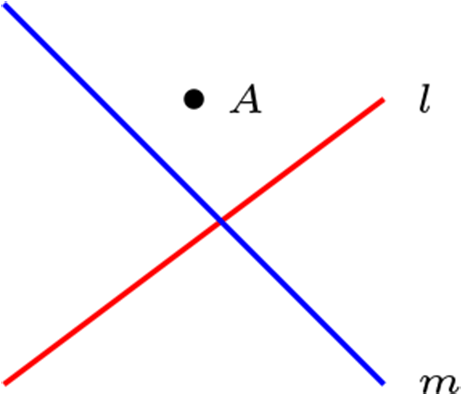
Sean \(P \in \mathcal{P}\text{ y } l \in \mathcal{L}\text{.}\) Si \(P {\not\mathcal{I}} l \text{ entonces } \exists ! m \in \mathcal{L}\) tal que \(P \mathcal{I}m \text{ y } m \parallel l\) (quinto postulado de Euclides).
-
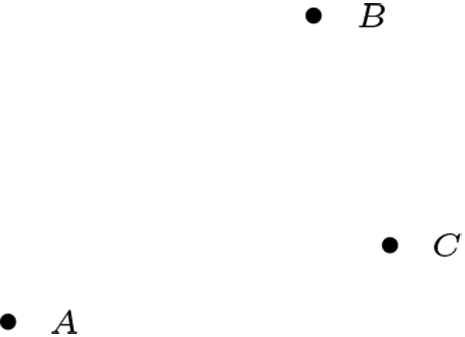
Existen tres puntos no colineales (no existe una recta tal que contenga a estos tres puntos) y cada recta inciden al menos dos puntos.
Teorema 1.2.2
Sea \(\Pi=(\mathcal{P},\mathcal{L},\mathcal{I})\) un plano afín, entonces la relación de paralelismo es una relación de equivalencia.
Demostración
-
\(\parallel\) es refleja, es decir, \((\forall l \in \mathcal{L})(l \parallel l)\text{,}\) para ello tenemos que
\begin{equation*}
l=l \text{, luego } l \parallel l.
\end{equation*}
-
\(\parallel\) es simétrica, es decir, \((\forall l, m \in \mathcal{L})(l \| m \Rightarrow m \parallel l)\)
Consideremos dos rectas paralelas \(l\parallel m\) luego se tiene que
\begin{equation*}
l \cap m =\ \phi\ \vee\ l=m
\end{equation*}
lo cual es equivalente a
\begin{equation*}
m \cap l = \phi\ \vee\ m=l,
\end{equation*}
es decir, \(m\parallel l\text{.}\)
-
\(\parallel\) es transitiva, es decir, \((\forall \ l,m,t \in \mathcal{L})(l\parallel m \wedge m \| t \Rightarrow l \parallel t)\text{.}\)
Lo cual demostraremos por el absurdo. Sean \(l,t,m\) tres rectas tales que \(l\parallel m \ , \ m \parallel t \text{ y } l\nparallel t\text{,}\) como \(l \nparallel t\) luego, \(l \neq t \text{ y }l \cap t = \{P\}\text{,}\) pero por \(P\) pasan dos rectas paralelas a \(m\) contradicción (unicidad del axioma dos). Por lo tanto la relación de paralelismo es una relación de equivalencia.
Definición 1.2.3
Plano afín minimal es aquel plano formado por el mínimo número de puntos que cumplen con los tres axiomas.
Proposición 1.2.4
Todo plano afín al menos contiene cuatro puntos.
Demostración
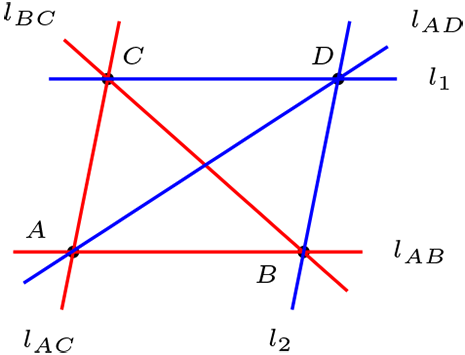
Por axioma tres sabemos que existen tres puntos no colineales \(A,B,C\text{,}\) del cual por axioma uno, existen tres rectas que unen a estos tres puntos que los definiremos como \(l_{AB},l_{BC},l_{AC}\) respectivamente como se observa en la imagen.
Consideremos la recta \(l_{AB}\text{,}\) por axioma dos tenemos que existe una recta paralela a \(l_{AB}\) que la designaremos por \(l_{1}\) y que pasa por el punto \(C\text{,}\) análogamente se prueba la existencia de una recta paralela a \(l_{AC}\) que pasa por \(B\) que llamaremos por \(l_{2}\text{,}\) como la recta \(l_{AB} \bigcap l_{AC} \neq \varnothing\) entonces también lo hacen las rectas \(l_{1}\) y \(l_{2}\) en el punto \(D\) y para concluir determinaremos la existencia de la recta \(l_{AD}\) que pasa respectivamente por los puntos \(A,D\text{.}\)
Ejemplo 1.2.6
Sea \(\mathcal{P}=\mathbb{Z}_{2}\times \mathbb{Z}_{2}\text{.}\) Determine las ecuaciones de las rectas y si existe paralelismo entre ellas.
Las ecuaciones de las rectas de \(\mathbb{Z}_{2} \times \mathbb{Z}_{2}\) están dada por
\begin{align*}
l_{1}:y=0 \amp \quad \amp l_{4}:x=0 \\
l_{2}:x=1 \amp \amp l_{5}:y=x \\
l_{3}:y=1 \amp \amp l_{6}:y=x+1
\end{align*}
En consecuencia \(l_{1}\|l_{3}, \ l_{2} \|l_{4}\) y \(l_{5}\|l_{6}\) (estas últimas son paralelas porque no hay ningún punto en común). \(\mathbb{Z}_{2} \times \mathbb{Z}_{2}\) es un modelo del plano afín minimal en donde \(\mathbb{Z}_{2} \times \mathbb{Z}_{2}\) es el espacio vectorial de dimensión dos.
Plano Afín Vectorial
Teorema 1.2.7
Sea \(\mathcal{V}\) un \(\mathbb{K}\)-espacio vectorial de dimension dos
Si los puntos son las vectores, las rectas son las rectas afines y la incidencia es la pertenecía entonces \(\Pi=(\mathcal{V}, \mathcal{L},\mathcal{I}) \text{,}\) es un Plano Afín.
Demostración
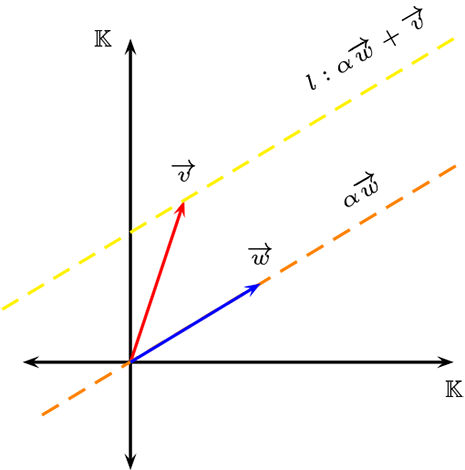
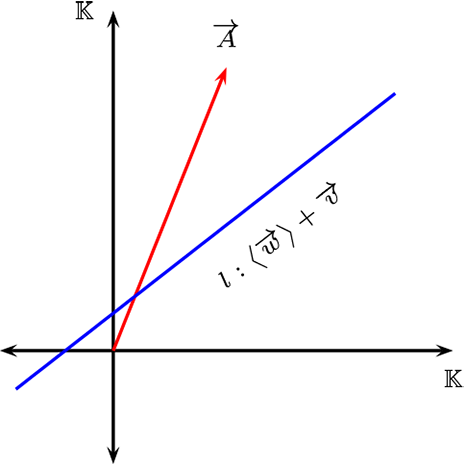
Sean \(\overrightarrow{v},\overrightarrow{w} \in \mathcal{V}\) con \(\overrightarrow{w} \neq 0\text{,}\) definamos la recta afines \(l\) en dirección \(\overrightarrow{w}\) y trasladada en \(\overrightarrow{v}\text{,}\) por \(l=\{ \alpha \overrightarrow{w}+\overrightarrow{v} \ | \ \alpha \in \mathbb{K} \}\)
Sea \(l=\{ \alpha \overrightarrow{w}+\overrightarrow{v} \ | \ \alpha \in \mathbb{K}\}\) una recta afín, por comodidad se denotara por
\begin{equation*}
l:\langle \overrightarrow{w}\rangle+\overrightarrow{v}.
\end{equation*}
La Incidencia esta definida por \(\overrightarrow{P} \ \mathcal{I} \ l \) es equivalente a \(\overrightarrow{P} \in l\text{.}\) De otro modo, existe \(\alpha \in \mathbb{K}\) tal que \(\overrightarrow{P}=\alpha \overrightarrow{w}+\overrightarrow{v}\text{.}\)
Verifiquemos los axiomas del plano afín.
-
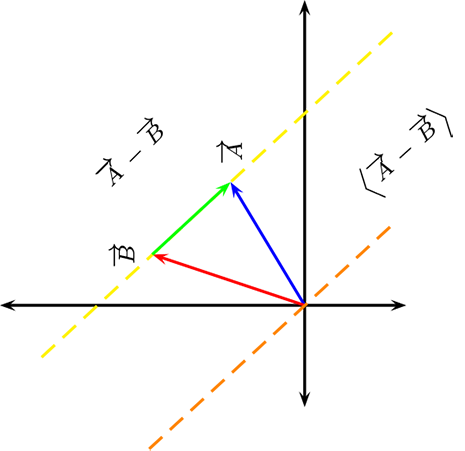
Sea \(\overrightarrow{A},\overrightarrow{B} \in \mathcal{V}\) con \(\overrightarrow{A} \neq \overrightarrow{B}\text{.}\) Debemos demostrar que existe \(m \in \mathcal{L}\) tal que \(\overrightarrow{A} \ \mathcal{I} \ m\) y \(\overrightarrow{B} \ \mathcal{I} \ m\text{.}\)
Para ello tenemos que \(\overrightarrow{A}-\overrightarrow{B} \neq \overrightarrow{0}\) y definamos
\begin{equation*}
m= \left\{ \alpha \left( \overrightarrow{A}-\overrightarrow{B} \right)+ \overrightarrow{A} \ | \ \alpha \in \mathbb{K} \right\},
\end{equation*}
luego tenemos que \(\overrightarrow{A}=0 \left( \overrightarrow{A}- \overrightarrow{B} \right)+\overrightarrow{A}\text{,}\) entonces \(\overrightarrow{A} \in m\text{,}\) es decir, \(\overrightarrow{A} \ \mathcal{I} \ m\text{.}\) Análogamente \(\overrightarrow{B}=(-1)\left( \overrightarrow{A}-\overrightarrow{B} \right)+ \overrightarrow{A}\text{,}\) es decir, \(\overrightarrow{B} \ \mathcal{I} \ m\text{.}\)
Unicidad: Supongamos que \(\exists t \in \mathcal{L}\) de modo que
\begin{equation*}
t=\left\{ \alpha \overrightarrow{w}+\overrightarrow{v} \ | \ \alpha \in \mathbb{K} \right\}
\end{equation*}
tal que \(\overrightarrow{A} \ \mathcal{I} \ t \text{ y } \overrightarrow{B} \ \mathcal{I} \ t\text{,}\) luego existe un \(\alpha_1,\alpha_2 \in \mathbb{K}\) distintos tales que
\begin{equation*}
\begin{array}{rcl|}
\overrightarrow{A} \amp = \amp \alpha_1 \overrightarrow{w}+\overrightarrow{v} \\
\overrightarrow{B} \amp = \amp \alpha_2 \overrightarrow{w}+\overrightarrow{v} \\ \hline
\end{array}
\end{equation*}
de lo cual
\begin{align*}
\overrightarrow{A}-\overrightarrow{B} \amp = \amp \alpha_1 \overrightarrow{w}-\alpha_2 \overrightarrow{w}+\overrightarrow{v}-\overrightarrow{v} \amp \\
\amp = \amp \alpha_1 \overrightarrow{w}-\alpha_2 \overrightarrow{w} \amp \\
\amp = \amp (\alpha_1-\alpha_2)\overrightarrow{w} \amp \\
\overrightarrow{A}-\overrightarrow{B} \amp = \amp \alpha_3 \overrightarrow{w} \amp \text{ con }\alpha_3 \neq 0 \\
\overrightarrow{w} \amp = \amp (\alpha_3)^{-1}\left( \overrightarrow{A}-\overrightarrow{B} \right) \amp
\end{align*}
Por lo tanto \(\left \langle \overrightarrow{w} \right\rangle = \left \langle \overrightarrow{A}-\overrightarrow{B} \right \rangle\) y \(\overrightarrow{A} \in t\cap m\text{,}\) luego \(t=m\text{.}\)
-
Sean \(\overrightarrow{A} \in \mathcal{V}, \ l \in \mathcal{L}\text{ y } \overrightarrow{A}\ {\not\mathcal{I}} \ l\text{.}\) Por demostrar que existe una recta \(m \in \mathcal{L}\) tal que \(\overrightarrow{A} \ \mathcal{I} \ m \wedge m \parallel l \text{.}\)
Sea \(l:\left\langle \overrightarrow{w}\right\rangle + \overrightarrow{v}\) la recta debe tener la misma dirección y contener al vector \(\overrightarrow{A}\text{,}\) entonces la recta \(m\) de define como:
\begin{equation*}
m:\left\langle \overrightarrow{w}\right\rangle + \overrightarrow{A}
\end{equation*}
Unicidad
Supongamos que \(\exists t \in \mathcal{L}\) tal que \(\overrightarrow{A}\mathcal{I}t , \ \overrightarrow{A}\mathcal{I}m\text{,}\) el cual definiremos como \(t:=\lt\overrightarrow{x}\gt + \overrightarrow{y}, m:=\lt\overrightarrow{w}\gt+\overrightarrow{A}\text{.}\)
Ya que \(\overrightarrow{A} \in t\) entonces \(t=\left\langle \overrightarrow{x}\right\rangle + \overrightarrow{A}\) pero \(t \parallel m\text{,}\) entonces \(\left\langle \overrightarrow{x}\right\rangle = \left\langle \overrightarrow{w}\right\rangle\) luego \(m=\left\langle \overrightarrow{x}\right\rangle+\overrightarrow{A}\) es decir,
\begin{align*}
t \amp = \amp \left\langle \overrightarrow{w}\right\rangle + \overrightarrow{A} \\
m \amp = \amp \left\langle \overrightarrow{w}\right \rangle + \overrightarrow{A}
\end{align*}
en consecuencia \(t=m\text{.}\)
-
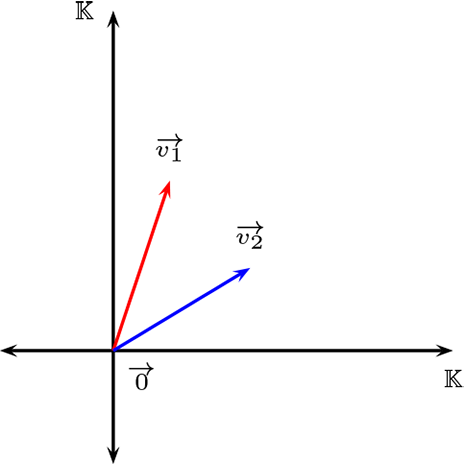
Por demostrar que existe un triángulo.
Sea \(B=\{\overrightarrow{v_{1}},\overrightarrow{v_{2}}\}\) base de \(\mathcal{V}\text{,}\) y \(\overrightarrow{0}\in \mathcal{V}\) entonces tenemos \(\overrightarrow{0},\overrightarrow{v_{1}},\overrightarrow{v_{2}}\) no son colineales, ya si \(l\) contiene a los tres elementos \(\overrightarrow{0} \in l\)
\begin{equation*}
l:\left\langle \overrightarrow{w}\right\rangle +\overrightarrow{0}
\end{equation*}
pero \(\overrightarrow{v_1},\overrightarrow{v_2}\in l\)
\begin{equation*}
\overrightarrow{v_1}=\alpha_1 \overrightarrow{w} \ , \ \overrightarrow{v_2}=\alpha_2 \overrightarrow{w}
\end{equation*}
luego \(\overrightarrow{v_1},\overrightarrow{v_2}\) son linealmente dependiente.
De este modo, existen tres puntos no colineales.
Por lo tanto \(\Pi=(\mathcal{V}, \mathcal{L},\mathcal{I}) \text{,}\) es un {\rm Plano Afín}
Ejemplo 1.2.8
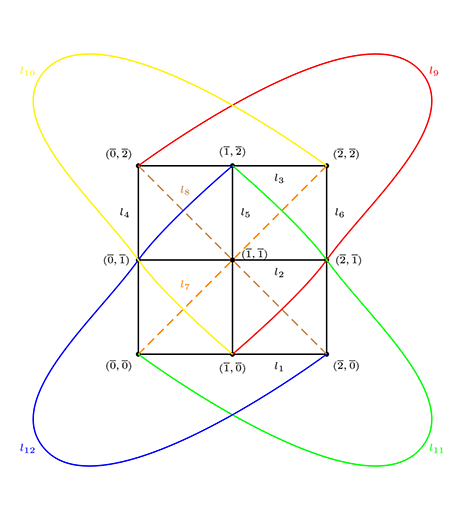
Sea \(\mathcal{P}=\mathbb{Z}_{3}\times\mathbb{Z}_{3}\text{.}\)
Determine las ecuaciones de las rectas y si existe paralelismo entre ellas.
Consideremos los puntos
\begin{equation*}
\mathcal{P}=\{(\overline{0},\overline{0}),(\overline{1},\overline{0}),(\overline{2},\overline{0}),
(\overline{0},\overline{1}),(\overline{1},\overline{1}),(\overline{2},\overline{1})
,(\overline{0},\overline{2}),(\overline{1},\overline{2}),(\overline{2},\overline{2})\}
\end{equation*}
las ecuaciones de las rectas son:
\begin{align*}
l_{1}:y=0, \amp\qquad \amp l_{4}:x=0, \amp\qquad\amp l_{7}: y=x, \amp\qquad \amp l_{10}:y=2x+1, \\
l_{2}:y=1, \amp \amp l_{5}:x=1, \amp \amp l_{8}: y=2x+3, \amp \amp l_{11}:y=2x, \\
l_{3}:y=2, \amp \amp l_{6}:x=2, \amp \amp l_{9}: y=x+2, \amp \amp l_{12}:y=x+1.
\end{align*}
Las rectas paralelas entre ellas son:
\begin{equation*}
l_{1}\|l_{2}\|l_{3}\text{ ; }l_{4}\|l_{5}\|l_{6}\text{ ; }l_{7}\|l_{9}\|l_{12} \text{ y }l_{8}\|l_{10}\|l_{11}
\end{equation*}
Definición 1.2.9
Dados los puntos \(P_1, P_2, \ldots, P_n\) se dice que los puntos son colineales si y sólo si existe \(l\in \mathcal{L}\) tal que \(P_i\mathcal{I}l\) para todo \(i=1,2,\ldots , n\text{.}\)