Sección 4.4 Funciones Trigonométricas en Triángulos
¶En esta sección veremos la utilidad de las funciones, para determinar los valores de los ángulos y la longitud de los lados en un triángulo cualquiera.
Subsección 4.4.1 Triángulo Rectángulo
¶Sean \(\alpha,a,b,c \in \mathbb{R}^{+}\text{,}\) tales que son las longitudes de un triángulo rectángulo, y \(\alpha\) es el ángulo de unos de los lados como en la figura.
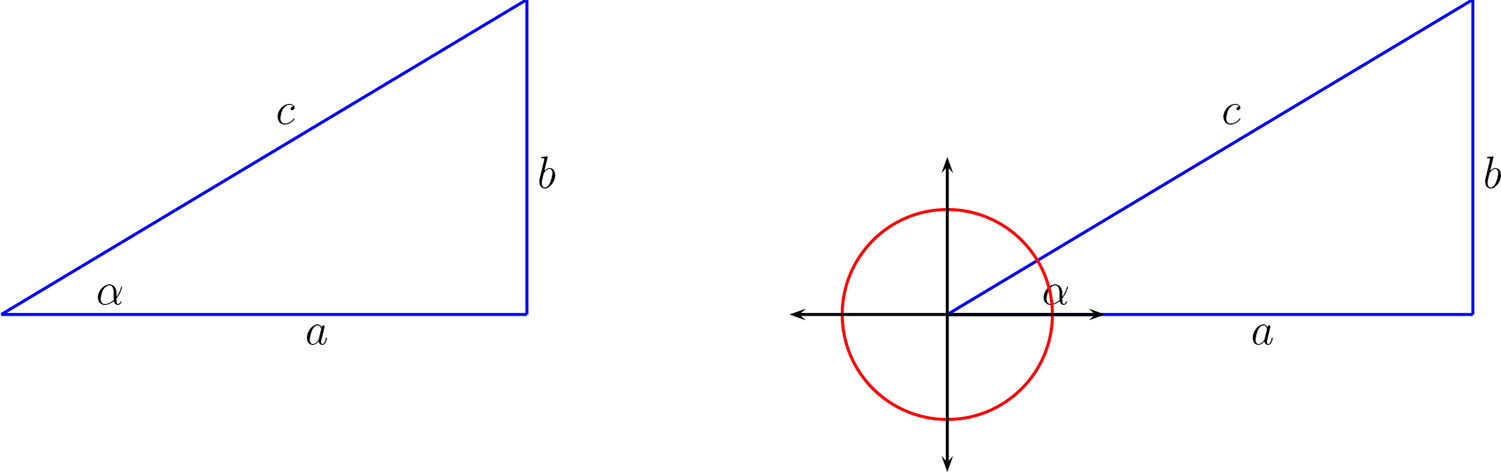
Podemos construir una circunferencia unitaria, con centro en el ángulo \(\alpha\) y por Thales tenemos
\begin{equation*}
\frac{\cos(\alpha)}{1} = \frac{a}{c}= \frac{cat.ady.}{hip.}
\end{equation*}
donde \(cat.ady.\) representa la longitud de cateto adyacente e \(hip\) es la longitud de la hipotenusa desde el ángulo \(\alpha\text{.}\)
Otra proporciones
\begin{equation*}
\frac{\sin(\alpha)}{1}=\frac{b}{c}
\end{equation*}
\begin{equation*}
\sin(\alpha) = \frac{b}{c}=\frac{cat.op.}{hip.}
\end{equation*}
donde \(cat.op.\) representa la longitud de cateto opuesto e \(hip.\) es la longitud de la hipotenusa en el triángulo desde el ángulo \(\alpha\text{.}\) y también tenemos otra proporciones
\begin{equation*}
\frac{\sin(\alpha)}{\cos(\alpha )}=\frac{b}{a}
\end{equation*}
\begin{equation*}
\tan(\alpha) = \frac{b}{a}=\frac{cat.op.}{cat.ady.}
\end{equation*}
La otras funciones las podemos describir por las siguientes proporciones:
\begin{equation*}
\cot(\alpha) = \frac{a}{b} = \frac{cat.ady.}{cot. op.} \ \ \ \ \
\sec(\alpha) = \frac{c}{a} = \frac{hip.}{cat.ady.} \ \ \ \ \
\csc(\alpha) =\frac{c}{b}= \frac{hip.}{cat.op.}
\end{equation*}
Los resultados anteriormente obtenidos nos sirven para poder resolver ejercicios como en el siguiente ejemplo.
En el rectángulo siguiente se ha inscrito la figura
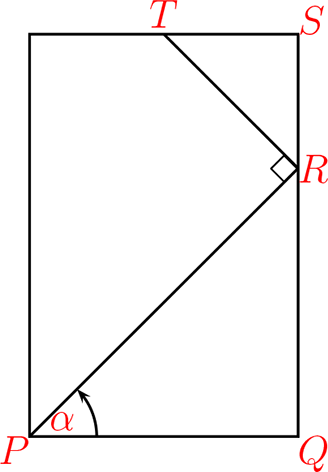
donde \(\overline{RS} = 1 cm, \ \overline{RQ} = 2 cm \) y el \(\measuredangle PRT = \frac{\pi}{2}\text{.}\)
Determine \(\alpha\) de manera que \(\overline{PR}\) sea el doble de \(\overline{TR}\text{.}\)
De la figura anterior, obtenemos
\begin{equation*}
\beta = \measuredangle \ TRS = \alpha
\end{equation*}
Para ello, notemos que \(\measuredangle \ PRQ = \frac{\pi}{2} - \alpha\) y \(\measuredangle \ TRS = \beta\) de donde tenemos
\begin{equation*}
\begin{array}{rcl}
\beta + \frac{\pi}{2} + \frac{\pi}{2} - \alpha \amp =\amp \pi
\end{array}
\end{equation*}
Luego \(\beta = \alpha\text{.}\) Entonces
\begin{equation*}
\begin{array}{rcl}
\cos(\alpha) = \cos(\beta) = \frac{\overline{RS}}{\overline{TR}}
= \frac{1}{\overline{TR}}
\end{array}
\end{equation*}
Por lo tanto
\begin{equation*}
\overline{TR}= \frac{1}{\cos(\alpha)}
\end{equation*}
Por otro lado tenemos
\begin{equation*}
\begin{array}{rcl}
\sin(\alpha) = \frac{\overline{RQ}}{\overline{PR}} = \frac{2}{\overline{PR}}
\end{array}
\end{equation*}
De lo cual
\begin{equation*}
\overline{PR} = \frac{2}{\sin(\alpha)}
\end{equation*}
Como debe tenerse que \(\overline{PR} = 2 \overline{TR}\) obtenemos
\begin{equation*}
\begin{array}{rcl}
\frac{2}{\sin(\alpha)} = 2 \frac{1}{\cos(\alpha)} \amp \text{de lo cual}, \amp \tan(\alpha) = 1
\end{array}
\end{equation*}
De este modo tenemos \(\alpha = \frac{\pi}{4}\text{.}\)
Subsección 4.4.2 Teorema del Seno
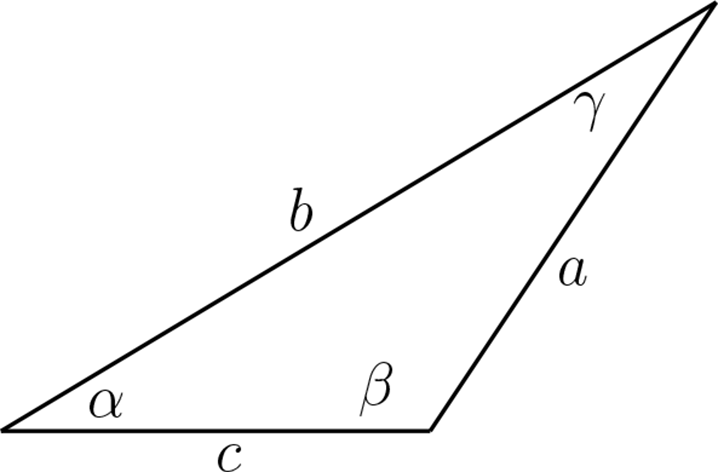
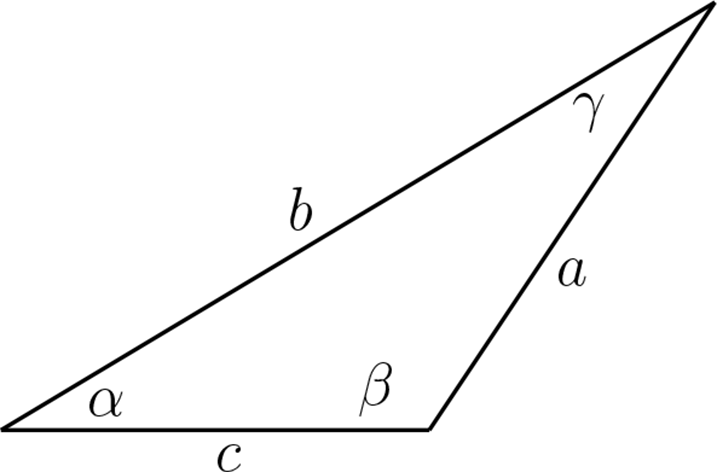
¶Sean \(\alpha,\beta,\gamma\) los ángulos internos de un triángulos arbitrario y \(a,b,c\) las longitudes de los lados como en la figura.
Tracemos una altura en el triángulo
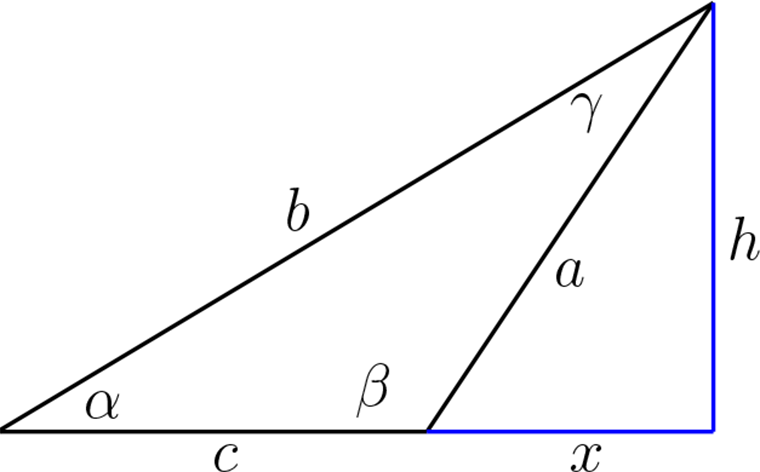
Sabemos que
\begin{equation*}
\sin(\alpha) = \frac{cat.op.}{hip.} = \frac{h}{b}
\end{equation*}
y además
\begin{equation*}
\sin (\pi-\beta) = \frac{cat.op}{hip.} = \frac{h}{a}
\end{equation*}
pero
\begin{equation*}
\sin(\pi-\beta)=\sin(\beta)
\end{equation*}
Despejando \(h\) e igualando tenemos
\begin{equation*}
h = b \sin(\alpha) =a\sin(\beta)
\end{equation*}
Por lo tanto
\begin{equation*}
\frac{\sin(\alpha)}{a} = \frac{\sin(\beta)}{b}
\end{equation*}
con un proceso similar obtenemos
\begin{equation*}
\frac{\sin(\alpha)}{a} = \frac{\sin(\gamma)}{c}
\end{equation*}
Igualando las dos expresiones obtenemos el teorema del seno
Teorema 4.4.2 [Teorema Ley del Seno]
Sean \(\alpha, \beta ,\gamma , a ,b,c \in \mathbb{R}\text{,}\) los ángulos interiores, y la longitudes de los lados de un triángulo, como en la figura
entonces se cumple que
\begin{equation*}
\frac{\sin(\alpha)}{a} = \frac{\sin(\beta)}{b} = \frac{\sin(\gamma)}{c}
\end{equation*}
o de igual manera
\begin{equation*}
\frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)}
\end{equation*}
Subsección 4.4.3 Teorema Ley del Coseno
¶Sean \(\alpha,\beta,\gamma\) los ángulos internos de un triángulos arbitrario y \(a,b,c\) las longitudes de los lados y además tracemos una altura como en la figura.
Usando el teorema de pitágoras en los triángulos tenemos
\begin{equation*}
a^{2} = h^{2} + x^{2}
\end{equation*}
y en el otro tenemos
\begin{equation*}
b^{2} = h^{2} + (c+x)^{2}
\end{equation*}
desarrollando el cuadrado de binomio,
\begin{equation*}
b^2=h^2+c^2+2cx+x^2
\end{equation*}
reemplazando obtenemos
\begin{equation*}
b^2=a^2+c^2+2cx
\end{equation*}
En el triángulo rectángulo se tiene
\begin{equation*}
-\cos(\beta)=\cos(\pi-\beta)=\frac{x}{a}
\end{equation*}
luego tenemos
\begin{equation*}
b^2=a^2+c^2+2c(-a\cos(\beta))
\end{equation*}
Teorema 4.4.3 [Ley del Coseno]
Sean \(\alpha, \beta ,\gamma , a ,b,c \in \mathbb{R}\text{,}\) los ángulos interiores, y la longitudes de los lados de un triángulo, como en la figura
entonces se cumple que
\begin{equation*}
\begin{array}{rcl}
a^{2} \amp =\amp b^{2} + c^{2} - 2bc \cos(\alpha) \\
b^{2} \amp =\amp a^{2} + c^{2} - 2ac \cos(\beta) \\
c^{2} \amp =\amp a^{2} + b^{2} - 2ab \cos(\gamma)
\end{array}
\end{equation*}
Subsección 4.4.4 Resolución de Triángulos
¶Es el proceso mediante el cual se obtiene las longitudes de los lados y la medida de los tres ángulos de un triángulo.
Por congruencia de triángulo, tenemos que las únicas cuatro posibilidades en que se obtiene un único triángulo son las siguientes.
Dados un lados y dos ángulos.
Dados dos lados y el ángulo comprendido entre ellos.
Dados dos lados y el ángulo opuesto al mayor.
Dados los tres lados.
En caso contrario, puede ocurrir que hay más de una solución o no existe el triángulo que cumpla las condiciones descrita en el problema.
Veamos ahora cada una de las esta situación, para ellos tengamos presente las notación de acuerdo a la siguiente figura:
Ejemplo 4.4.4 [Primer Caso]
Con las notaciones de la figura, sean \(a,\alpha,\beta\) conocidos.
Determinar \(b,c,\gamma\)
Como \(\alpha +\beta+\gamma = 180^\circ,\) luego \(\gamma = 180^\circ-\alpha -\beta.\)
Además por Ley de los Seno
\begin{equation*}
\frac{\sin(\alpha)}{a}=\frac{\sin(\gamma)}{c},\ \ \ \ \ \frac{\sin(\beta)}{b}=\frac{\sin(\gamma)}{c}.
\end{equation*}
de lo cual
\begin{equation*}
c=\frac{a\sin(\gamma)}{\sin(\alpha)},\ \ \ \ \ b=\frac{a\sin(\beta)}{\sin(\alpha)}.
\end{equation*}
Ejemplo 4.4.5 [Segundo Caso]
Con las notaciones de la figura, sean \(a,b,\gamma\) conocidos.
Determinar \(c,\alpha,\beta\)
Por la ley del Coseno tenemos
\begin{equation*}
c^{2} = a^{2} + b^{2} - 2ab \cos(\gamma)
\end{equation*}
luego
\begin{equation*}
c =\sqrt{a^{2} + b^{2} - 2ab \cos(\gamma)}
\end{equation*}
Además por Ley de los Seno
\begin{equation*}
\sin(\alpha)=\frac{a\sin(\gamma)}{c}
\end{equation*}
tiene dos soluciones menores que \(180^\circ\) y esta son
\begin{equation*}
\alpha=\arcsin\left(\frac{a\sin(\gamma)}{c}\right)\qquad \alpha=180^\circ- \arcsin\left(\frac{a\sin(\gamma)}{c}\right)
\end{equation*}
Además
\begin{equation*}
\beta=180^\circ-\alpha-\gamma,
\end{equation*}
que nos entregan el mismo triángulo.
Ejemplo 4.4.6 [Tercer Caso]
Con las notaciones de la figura, sean \(a,c,\gamma\text{,}\) \(a \lt c\) conocidos.
Determinar \(b,\alpha,\beta\)
Por ley del seno y además \(\frac{a\sin(\gamma)}{c} \lt 1\text{,}\) luego
\begin{equation*}
\alpha=\arcsin\left(\frac{a\sin(\gamma)}{c}\right)
\end{equation*}
de lo cual
\begin{equation*}
\beta = 180^\circ-\alpha -\gamma
\end{equation*}
Además por Ley de los Seno
\begin{equation*}
b=\frac{c\sin(\beta)}{\sin(\gamma)}
\end{equation*}
Ejemplo 4.4.7 [Cuarto Caso]
Con las notaciones de la figura, sean \(a,b,c\) conocidos.
Determinar \(\alpha,\beta,\gamma\)
Por la ley del Coseno tenemos
\begin{equation*}
c^{2} = a^{2} + b^{2} - 2ab \cos(\gamma)
\end{equation*}
luego
\begin{equation*}
\cos(\gamma) =\frac{a^{2} + b^{2} - c^2}{2ab}
\end{equation*}
\begin{equation*}
\gamma =\arccos\left(\frac{a^{2} + b^{2} - c^2}{2ab}\right)
\end{equation*}
análogamente
\begin{equation*}
\alpha=\arccos\left(\frac{b^{2} + c^{2} - a^2}{2bc}\right), \ \
\ \ \ \beta=\arccos\left(\frac{a^{2} + c^{2} - b^2}{2ac}\right).
\end{equation*}
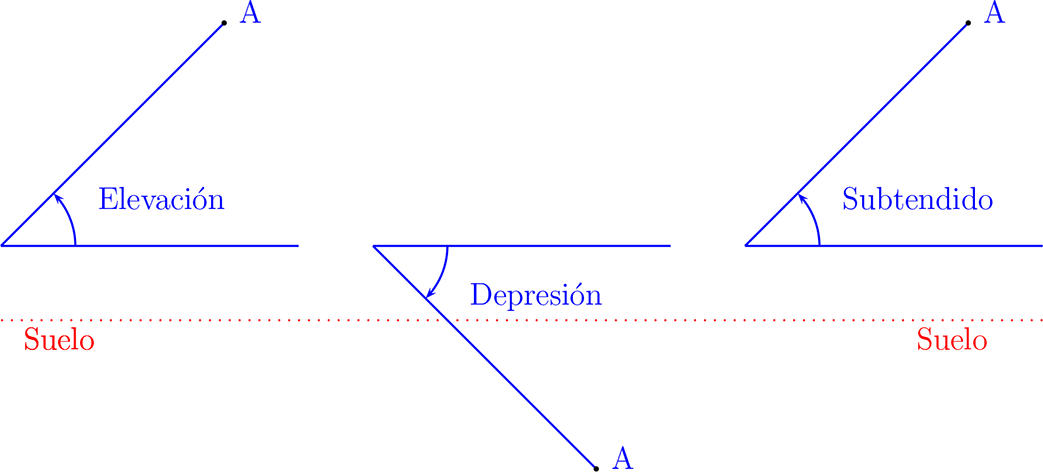
Observación: Para poder resolver algunos problemas de planteo es necesario tener claro algunos términos empleado al referirnos a ciertos ángulos.
ángulo de elevación: Es el ángulo formado por la línea del horizonte del observador y la línea formada por el observador y el objeto observado sobre el horizonte.
ángulo de depresión: Es el ángulo formado por la linea del horizonte del observador y la línea formada por el observador y el objeto observado bajo el horizonte.
ángulo subtendido: El ángulo subtendido por un objeto es el ángulo formado por la línea del horizonte del observador y la línea formada por el observador y el objeto observado.
Ejemplo 4.4.8
Cuando el sol esta a \(25^\circ 36'\) sobre el horizonte un silo da una sombra de \(28\) metros. Calcular la altura del silo.
Grafiquemos el problema,
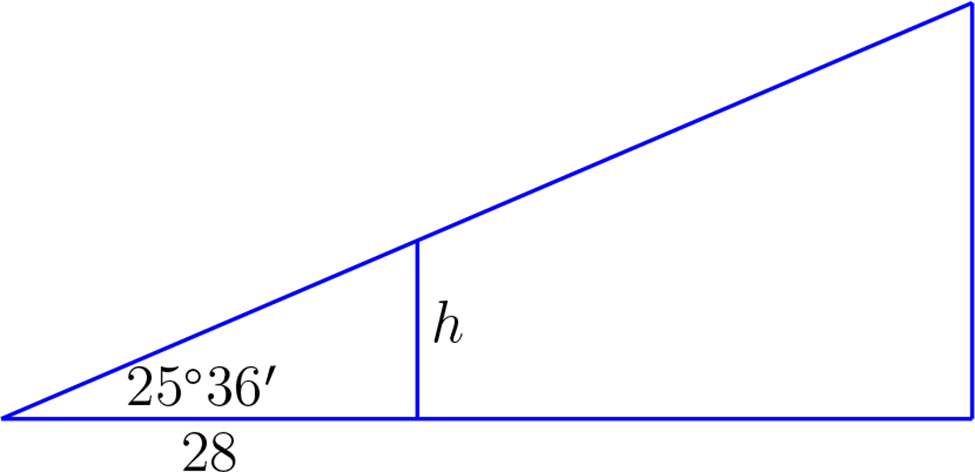
Calculando tangente se obtiene que
\begin{equation*}
\tan (25^\circ 36')= \frac{h}{28}
\end{equation*}
es decir, \(h= 28 \tan(25^\circ 36')=28\tan(25,6^\circ)\approx 13.4153. \)
La altura del silo aproximadamente es \(13.4153mts\)