Definición 2.2.1
Sean \(P,Q \in \mathbb{R}^{2}\text{,}\) con \(P=(x_{1},y_{1})\) y \(Q=(x_{2} , y_{2})\) entonces la distancia entre los dos puntos es
\begin{equation*}
dist(P,Q) = \sqrt{(x_{2}-x_{1})^{2} + (y_{2} - y_{1})^{2}}
\end{equation*}
Sección 2.2 Plano Cartesiano
¶Iniciamos este estudio, recordándonos las nociones básicas de plano cartesiano.
Para ello tenemos que el producto cartesiano esta dado por
\begin{equation*}
\mathbb{R} \times \mathbb{R} = \mathbb{R}^{2}
:= \{ (x,y) \mid x \ , y \in \mathbb{R} \}
\end{equation*}
Un elemento de \(\mathbb{R}^{2}\text{,}\) es un par ordenado \((x,y)\text{,}\) donde \(x\) es la primera coordenada o abscisa e \(y\) es la segunda coordenada u ordenada del punto \((x,y)\)
Además dos puntos en el producto cartesiano son iguales si y sólo si las abscisa y ordenadas son iguales, es decir, se cumple que
\begin{equation*}
(\forall x,y,x',y' \in \mathbb{R})\ (x,y)=(x',y') \Leftrightarrow (x=x' \wedge y=y')
\end{equation*}
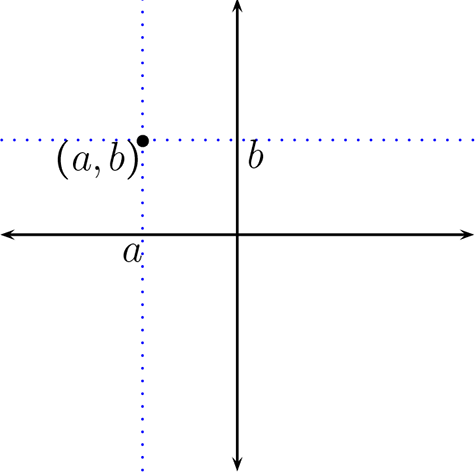
Un representación del producto cartesiano es el plano cartesiano, que se construye con dos rectas perpendiculares (ejes, un horizontal y otro vertical) que se intersecan en un punto(origen), un elemento del producto cartesiano, se representa con la intersecarse de la recta vertical que pasa por el eje horizontal en el valor de la abscisa y una horizontal que pasa por el eje vertical en el valor de la ordenada
Subsección 2.2.1 Distancia entre dos Puntos
¶La distancia entre dos puntos, corresponde asignarle un valor numérico no negativo al segmento que une estos dos puntos. Esta designación debería cumplir algunas propiedades, básicamente estas son que la distancia o longitud entre puntos iguales es cero, que la distancia no depende del sentido en que se mida y la longitud entre dos puntos es menor que la longitud que se obtiene por la vía de más segmentos.
En la recta real \(\mathbb{R}\text{,}\) la distancia entre dos puntos esta dada por
\begin{equation*}
dist(a,b) = \vert b - a \vert \hspace{1cm} \text{con} \ \ \ a,b
\in \mathbb{R}
\end{equation*}
la cual cumples las tres propiedades básicas anteriores.
Para extender esta definición al plano cartesiano, usaremos el teorema de Pitágoras de modo obtener una fórmula para la distancia entre dos puntos en el plano.
Sean \(P,Q \in \mathbb{R}^{2}\text{,}\) donde \(P=(x_{1},y_{1}), Q=(x_{2},y_{2})\text{.}\) La distancia entre ellos la denotaremos por \(dist(P,Q)\)
Grafiquemos los puntos \(P,Q\) en el plano cartesiano, y tracemos un triángulo rectángulo, con las rectas paralelas a los ejes coordenados.
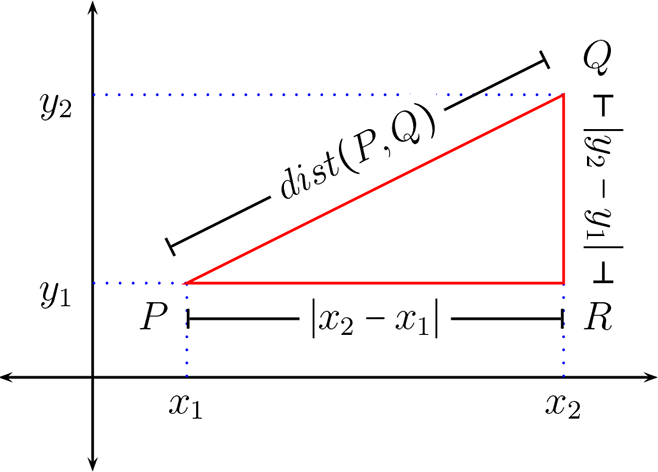
Luego por teorema de Pitágoras tenemos que
\begin{equation*}
(\mbox{hipotenusa})^{2} = (\mbox{cateto opuesto})^{2} + (\mbox{cateto adyacente})^{2}
\end{equation*}
Observación: Recordemos que la hipotenusa representa el lado que se encuentra opuesto al ángulo de \(90^\circ\) en la figura, el cateto opuesto que esta representado por la base del triángulo y cateto adyacente el lado restante.
\begin{equation*}
\begin{array}{lcclc}
\amp (\text{hipotenusa})^{2} \amp =\amp (\text{cateto opuesto})^{2} + (\text{cateto adyacente})^{2} \amp \\
\text{donde} \amp (dist(P,Q))^{2} \amp =\amp (x_{2}-x_{1})^{2} + (y_{2} - y_{1})^{2} \amp / \sqrt{} \\
\text{entonces} \amp \vert dist(P,Q) \vert \amp =\amp \sqrt{(x_{2}-x_{1})^{2} + (y_{2} - y_{1})^{2}} \\
\end{array}
\end{equation*}
Observación: La distancia representa una longitud, por lo cual está siempre es no negativa.
Ejemplo 2.2.2
Considere los puntos \((-2,-1)\) y \((2,2)\) en \(\mathbb{R}^{2}\text{,}\) calcule la distancia entre ellos.
Denotemos los puntos de la siguiente forma:
\begin{equation*}
A=(-2,-1) \ y \ B=(2,2)
\end{equation*}
luego calculemos la distancia entre ellos
\begin{equation*}
\begin{array}{rcl}
dist(A,B) \amp =\amp \sqrt{(2- (-2))^{2} + (2- (-1))^{2}} \\
\amp =\amp \sqrt{(2+2)^{2} + (2+1)^{2}} \\
\amp =\amp \sqrt{(4)^{2} + (3)^{2}} \\
\amp =\amp \sqrt{16 + 9} \\
\amp =\amp \sqrt{25} =5
\end{array}
\end{equation*}
Por lo tanto, la distancia que existe entre los puntos \(A=(-2,-1)\) y \(B=(2,2)\) es \(5\text{,}\) o bien
\begin{equation*}
dist(A,B)=5.
\end{equation*}
Proposición 2.2.3
Sean \(P,Q,R \in \mathbb{R}^{2}\) entonces
\(dist(P,Q) = 0\) es equivalente a \(P=Q\text{.}\)
\(dist(P,Q)= dist(Q,P)\text{.}\)
\(dist(P,Q) \leq dist(P,R) + dist(R,Q)\text{.}\)
Ejemplo 2.2.4
Demuestre que los puntos \((-2,-1),(2,2),(5,-2)\) son los vértices de un triángulo isósceles
Sean los puntos \(A=(-2,-1) , B=(2,2) \ \text{y} \ C=(5,-2)\) en \(\mathbb{R}^{2}\text{.}\)
Sabemos que \(dist(A,B)= 5\text{,}\) calculada en el ejemplo anteriormente, entonces ahora calcularemos las distancias faltantes para verificar si \(A,B\) y \(C\) son los vértices de un triángulo isosceles.
\begin{equation*}
\begin{array}{rcl}
dist(A,C) \amp =\amp \sqrt{(5-(-2))^{2} + (-2-(-1))^{2}} \\
\amp =\amp \sqrt{49 + 1} = \sqrt{50} = 5 \sqrt{2}
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{rcl}
dist(B,C) \amp =\amp \sqrt{(5-2)^{2} + (-2-2)^{2}} \\
\amp =\amp \sqrt{9 + 16}= \sqrt{25} = 5
\end{array}
\end{equation*}
En resumen se tiene lo siguiente
\begin{equation*}
dist(A,B) = dist(B,C)=5,\ \ dist(A,C)=5\sqrt{2}.
\end{equation*}
por lo tanto concluimos que los segmentos que se encuentran entre los puntos \(A,B\) y \(C\) forman un triángulo isósceles y no es equilátero.
Observación: Recordemos que un triángulo es isósceles cuando tiene dos lados de igual longitud.
Ejemplo 2.2.5
Encuentre todos los puntos que pertenecen a \(\mathbb{R}^{2}\) y que están a una distancia igual a \(1\) del origen \((0,0)\text{.}\)
Sea \(P=(x,y) \in \mathbb{R}^{2}\) tal que \(dist(Q,P) = 1\text{,}\) donde \(Q =(0,0)\text{.}\) Como
\begin{equation*}
\begin{array}{cccc}
dist(Q,P) \amp =\amp 1 \amp \\
\sqrt{(x-0)^{2} + (y-0)^{2}} \amp =\amp 1 \amp \\
\sqrt{x^{2} + y^{2}} \amp =\amp 1 \amp / ()^{2} \\
x^{2} + y^{2} \amp =\amp 1 \\
x^{2} \amp =\amp 1 - y^{2} \\
\end{array}
\end{equation*}
Ahora veremos cuales son esos punto, como \(x^{2} = 1 - y^{2}\text{,}\) donde \(x^{2}\) representa un número positivo, luego para que se cumpla la igualdad \(1- y^{2}\) también debe ser positivo, por lo tanto:
\begin{equation*}
\begin{array}{rcl}
1 - y^{2} \amp \geq \amp 0 \\
y^{2} \amp \leq \amp 1 \ \ \sqrt{} \\
\vert y \vert \amp \leq \amp 1
\end{array}
\end{equation*}
De este modo se tiene que \(y \in [-1,1]\) entonces
\begin{equation*}
\begin{array}{cccccc}
x^{2} \amp =\amp 1 - y^{2} \amp \sqrt{}\amp \\
x \amp =\amp \pm \sqrt{1 - y^{2}}
\end{array}
\end{equation*}
Por lo tanto
\begin{equation*}
P=(x,y)=(\sqrt{1-y^{2}} , y) \text{ o }\ P=(x,y)=(- \sqrt{1-y^{2}} , y) \ \ \text{con} \ y \in [-1,1].
\end{equation*}
Observación: La ecuación \(x^{2} + y^{2} = 1\) gráficamente corresponde a una circunferencia unitaria o de radio \(1\text{,}\) ya que son todos los puntos que están a una unidad de origen, figura que estudiaremos más adelante en este capítulo.
Subsección 2.2.2 Punto Medio
¶Definición 2.2.6
Dados \(P_{1},P_{2} \in \mathbb{R}^{2}\text{,}\) los extremos de un segmento, se dice que \(R\) es el punto medio del segmento \(\overline{PQ}\) si y sólo si
\begin{equation*}
dist(P_{1},R) = dist(R,P_{2})
\end{equation*}
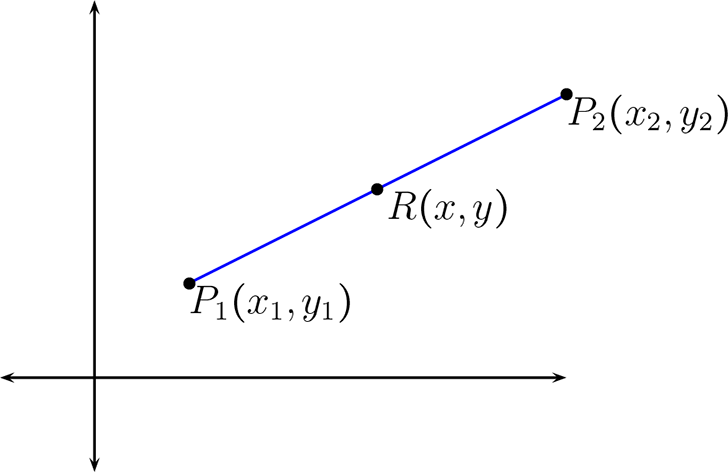
Aún más general, se tiene que
Definición 2.2.7
Sean \(P_{1},P_{2},R \in \mathbb{R}^{2} \text{,}\) se dice que \(R\) divide al segmento \(\overline{P_{1}P_{2}}\) en la razón \(r\) si y sólo si
\begin{equation*}
r = dist(P_{1},R) : dist(R,P_{2}).
\end{equation*}
Esto quiere decir:
\begin{equation*}
r = \frac{dist(P_{1},R)}{dist(R,P_{2})} .
\end{equation*}
Determine las coordenadas de punto que cumple tal condición
Sean \(P_{1}=(x_{1},y_{1}), P_{2}=(x_{2},y_{2})\) y \(R=(x,y)\text{,}\) de modo que satisface la siguiente razón
\begin{equation*}
r = \frac{dist(P_{1},R)}{dist(R,P_{2})}.
\end{equation*}
Apliquemos thales, en la siguiente figura
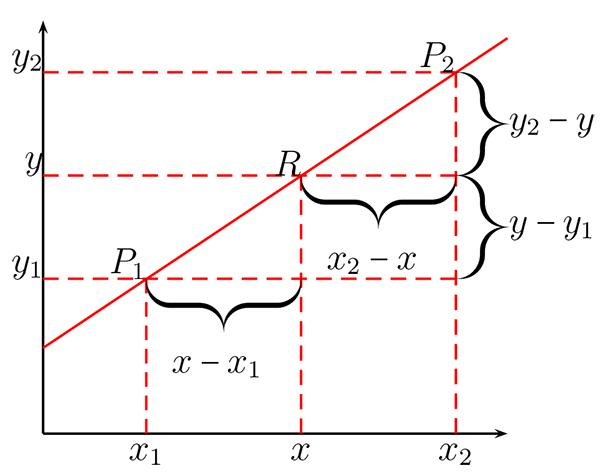
luego obtenemos que
\begin{equation*}
r = \frac{dist(P_{1},R)}{dist(R,P_{2})} = \frac{x - x_{1}}{x_{2}- x}.
\end{equation*}
Despejando \(x\) obtenemos
\begin{equation*}
\begin{array}{rcl}
r \amp =\amp \frac{x - x_{1}}{x_{2} - x} \\
r(x_{2} - x) \amp =\amp x - x_{1} \\
x + rx \amp =\amp r x_{2} + x_{1} \\
x(1+r) \amp =\amp r x_{2} + x_{1} \\
x \amp =\amp \frac{r x_{2} + x_{1} }{1+r}
\end{array}
\end{equation*}
Análogamente
\begin{equation*}
r = \frac{dist(P_{1},R)}{dist(R,P_{2})} = \frac{y- y_{1}}{y_{2} - y}
\end{equation*}
Despejando \(y\) obtenemos
\begin{equation*}
\begin{array}{rcl}
r \amp =\amp \frac{y - y_{1}}{y_{2} - y} \\
y \amp =\amp \frac{r y_{2} + y_{1} }{1+r}
\end{array}
\end{equation*}
Así obtenemos que las coordenadas de \(R\) son:
\begin{equation*}
R=(x,y) =\left( \frac{ rx_{2} + x_{1} }{1+r} ,\ \frac{ ry_{2} + y_{1} }{1+r} \right)
\end{equation*}
El caso particular en que \(r=1\text{,}\) se tiene el punto medio, y esta dado por:
\begin{equation*}
M=(x,y) = \left( \frac{ x_{2} + x_{1} }{2}, \ \frac{ y_{2} + y_{1} }{2} \right)
\end{equation*}
Proposición 2.2.8
Sean \(P_{1},P_{2} \ \text{y} \ M \in \mathbb{R}^{2}\text{,}\) tenemos que el punto medio del segmento \(\overline{P_{1}P_{2}}\) esta dado por:
\begin{equation*}
\label{punto medio}
M = \left( \frac{ x_{2} + x_{1} }{2} , \frac{ y_{2} + y_{1} }{2}
\right)
\end{equation*}
donde \(P_{1}=(x_{1},y_{1})\) y \(P_{2}=(x_{2},y_{2})\text{.}\)
Ejemplo 2.2.9
Encuentre el punto medio del segmento \(\overline{AB}\) donde \(A=(5,3)\) y \(B=(-10,-2)\)
Calculemos separadamente \(x\) e \(y\)
\begin{equation*}
x = \frac{ x_{2} + x_{1} }{2}=\frac{ -10 + 5}{2}=-\frac{5}{2}
\end{equation*}
\begin{equation*}
y = \frac{ y_{2} + y_{1} }{2} = \frac{ -2 + 3}{2} = \frac{ 1}{2}
\end{equation*}
Por lo tanto el punto medio del segmento \(\overline{AB}\) es el punto \((-\frac{5}{2},\frac{ 1}{2})\text{.}\)
Subsección 2.2.3 Puntos Colineales
¶Sean \(P_{1} =(x_{1},y_{1}) , P_{2} = (x_{2} , y_{2}) \) y \(P_{3} = (x_{3} , y_{3}) \in \mathbb{R}^{2}\text{,}\) por propiedad Proposición 2.2.3 de distancia obtenemos
\begin{equation*}
dist(P_{1},P_{3}) \leq dist(P_{1},P_{2}) + dist(P_{2},P_{3}) .
\end{equation*}
Observando la gráfica
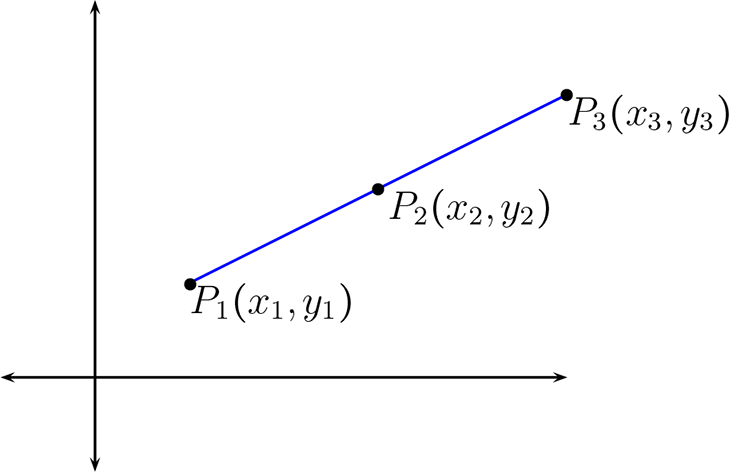
Se tiene que \(dist(P_{1},P_{3}) = dist(P_{1},P_{2}) + dist(P_{2},P_{3}) \text{,}\) luego
\begin{equation*}
\begin{array}{rcl}
dist(P_{1},P_{3}) \amp =\amp \sqrt{(x_{3} - x_{1})^{2} + (y_{3}-y_{1})^{2}} \\
dist(P_{1},P_{2}) \amp =\amp \sqrt{(x_{2} - x_{1})^{2} + (y_{2}-y_{1})^{2}} \\
dist(P_{2},P_{3}) \amp =\amp \sqrt{(x_{3} - x_{2})^{2} +
(y_{3}-y_{2})^{2}}
\end{array}
\end{equation*}
entonces
\begin{equation*}
\begin{array}{rcl}\label{a_11}
dist(P_{1},P_{3}) \amp =\amp dist(P_{1},P_{2}) + dist(P_{2},P_{3}) \\
\sqrt{(x_{3} - x_{1})^{2} + (y_{3}-y_{1})^{2}} \amp =\amp \!\!\!\!
\sqrt{(x_{2} - x_{1})^{2} + (y_{2}-y_{1})^{2}}\! + \!\!
\sqrt{(x_{3} - x_{2})^{2} + (y_{3}-y_{2})^{2}}
\end{array}
\end{equation*}
Consideremos los siguientes cambio de variables
\begin{equation*}
a = x_{2} - x_{1}, \qquad b = x_{3} - x_{2},
\end{equation*}
de lo cual se tiene que \(x_{3} - x_{1} = a+b\text{.}\)
De manera similar definimos
\begin{equation*}
c = y_{2} - y_{1}, \qquad d = y_{3} - y_{2}.
\end{equation*}
y obtenemos que \(y_{3} - y_{1} = c+d\)
Reemplazando, de modo de facilitar la simplificación, se obtiene
\begin{equation*}
\begin{array}{ccll}
\sqrt{(a+b)^{2} + (c+d)^{2}} \amp =\amp \sqrt{a^{2} + c^{2}} + \sqrt{b^{2} + d^{2}} \ \ /()^{2} \\
(a+b)^{2} + (c+d)^{2} \amp =\amp a^{2} +c^{2} +2 \sqrt{(a^{2} + c^{2})(b^{2} + d^{2})} + b^{2} + d^{2} \\
a^{2} + 2ab + b^{2} + c^{2} + 2cd + d^{2} \amp =\amp a^{2} + c^{2} + 2 \sqrt{(a^{2} + c^{2})(b^{2} + d^{2})} + b^{2} + d^{2} \\
2ab + 2cd \amp =\amp 2 \sqrt{(a^{2} + c^{2})(b^{2} + d^{2})} \amp / \frac{1}{2} \\
ab + cd \amp =\amp \sqrt{(a^{2} + c^{2})(b^{2} + d^{2})} \\
a^{2} b^{2} + 2abcd + c^{2}d^{2} \amp =\amp (a^{2} + c^{2})(b^{2} + d^{2}) \\
a^{2} b^{2} + 2abcd + c^{2}d^{2} \amp =\amp a^{2} b^{2} + a^{2}d^{2} + c^{2} b^{2} + c^{2} d^{2} \\
2abcd \amp =\amp a^{2}d^{2} + c^{2} b^{2} \\
a^{2}d^{2} - 2abcd + c^{2} b^{2} \amp =\amp 0 \\
(ad - cb)^{2} \amp =\amp 0
\end{array}
\end{equation*}
Entonces \(ad - cb = 0\text{,}\) volvemos a las variables originales que son
\begin{equation*}
a = x_{2} - x_{1}, \quad c = y_{2} - y_{1},\quad b = x_{3} - x_{2}, \quad d = y_{3} - y_{2}
\end{equation*}
Por lo tanto, obtenemos
\begin{equation*}
\begin{array}{rcl}
ad \amp =\amp cb \\
(x_{2} - x_{1})(y_{3} - y_{2}) \amp =\amp (y_{2} - y_{1})(x_{3} - x_{2})
\end{array}
\end{equation*}
Definición 2.2.10
Sean \(P_{1},P_{2},P_{3} \in \mathbb{R}^{2}\text{,}\) diremos que \(P_{1}=(x_{1},y_{1}) , P_{2}=(x_{2}, y_{2})\) y \(P_{3} =(x_{3},y_{3})\) son colineales si y sólo si
\begin{equation*}
dist(P_{1},P_{3}) = dist(P_{1},P_{2}) + dist(P_{2},P_{3}) \ \ \ \ \text{o bien} \ \ \ \ (x_{2} - x_{1})(y_{3} - y_{2}) = (y_{2} - y_{1})(x_{3} - x_{2})
\end{equation*}
Ejemplo 2.2.11
Encuentre el conjunto de todos los puntos colineales a \(P=(13,3)\) y \(Q=(9,15).\)
Sean \(P,Q\) y \(R\) colineales, luego por la definición anterior se tiene que
\begin{equation*}
dist(P,Q) = dist(P,R) + dist(R,Q)
\end{equation*}
\begin{equation*}
(x_{2} - x_{1})(y_{3} - y_{2}) = (y_{2} - y_{1})(x_{3} - x_{2})
\end{equation*}
En este ejemplo tenemos que \(P = (13,3) = (x_{1} , y_{1}); Q = (9,15) = (x_{3} , y_{3})\) y \(R = (x_{2} , y_{2}) = (x,y)\) entonces obtenemos
\begin{equation*}
\begin{array}{rcl}
(x - 13)(15 - y) \amp =\amp (y - 3)(9 - x) \\
15x - xy - 195 + 13y \amp =\amp 9y - xy -27 + 3x \\
12x + 4y \amp =\amp 168 \\
y \amp =\amp \frac{168 - 12x}{4} \\
y \amp =\amp 42 - 3x
\end{array}
\end{equation*}
Por lo tanto \(R \in \{ (x,y)\in\mathbb{R}\ | \ y= 42 - 3x \}\text{.}\)