Mat Ejercicios Propuestos

Sección 1.6 Ejercicios Propuestos

Grupos
1. En $\mathbb{Z}$ se define la operación $*$ por:
  
  \begin{equation*} x*y=xy+x+y. \end{equation*}
  
  Decida si $\mathbb{Z}$ bajo esta operación es un grupo.
2. Sean $G=\{(x,y)\,\,|\,\,x\in \mathbb{Q} \wedge y\in \mathbb{Z}\}$ y $*$ la operación definida por:
  
  \begin{equation*} (x,y)*(x^{'},y^{'})=(xx^{'},y+y^{'}) \end{equation*}
  
  Decida si $G$ bajo esta operación es un grupo.
3. Sea $G=\{ax^2+bx+c\,\,|\,\,a,b,c\in \mathbb{R}\}\text{,}$ se define la suma
  
  \begin{equation*} (ax^2+bx+c)+(a^{'}x^2+b^{'}x+c^{'})=(a+a^{'})x^2+(b+b^{'})x+(c+c^{'}) \end{equation*}
  
  Demuestre que $G$ bajo esta operación es un grupo abeliano.
4. Sea $G$ un grupo. Demuestre que para todo $a,b\in G\text{,}$ la ecuación
  
  \begin{equation*} ax=b \end{equation*}
  
  tiene única solución.
5. Sea $G$ un grupo y $H$ un subconjunto no vacío de $G\text{.}$ Se dice que $H$ es un subgrupo de $G$ si y sólo si las siguientes condiciones se satisfacen
  1. $(\forall a,b\in H)(ab\in H)$
  2. $(\forall a\in H)(a^{-1}\in H)$
  De acuerdo a esto demuestre que:
  1. $(\mathbb{Q},+)$ es un subgrupo de $(\mathbb{R},+)\text{.}$
  2. $Z=\{g\in G\,\,|\,\,(\forall h\in G)(gh=hg)\}$ es un subgrupo de $G\text{.}$
Resolver las siguientes ecuaciones
1. $\dfrac{x+1}{x-1} +\dfrac{x+2}{x+1}= \dfrac{1}{x+3}$
2. $\sqrt{x-3}+ x=6$
3. $\sqrt{4x^2-1}+\sqrt{27-3x^2}=|x|+ 5$
4. $\sqrt{x-5}+\sqrt{7-x}=|x-3|$
5. $\sqrt{\sqrt{x}+3}-\sqrt{\sqrt{x}-3}=\sqrt{2\sqrt{x}}$
6. $x+\sqrt{6-4x^2-x}=4x^2$
7. $\sqrt{|x+1|-6}= 8x-x^2-15$
8. $x-1=\sqrt{x^2-x+2}$
9. $||2x+3|-|x-3||=|3x+2|+ x$
10. $||2x+1||= 2x$
11. $\dfrac{x-5}{x^2-9}+\dfrac{x+3}{x-3}=1$
12. $\dfrac{x}{x^2-4}-\dfrac{x+2}{x-2}=1$
13. $\dfrac{x+m}{m}-\dfrac{x+n}{n}=\dfrac{m^2+n^2}{mn}-2$
14. $\left(\dfrac{x+\frac{b-x}{1+bx}}{1-\frac{x(b-x)}{1+bx}}- \dfrac{b-\frac{b-x}{1-bx}}{1- \frac{b(b-x)}{1-bx}}\right)^{-1} \cdot \left( \dfrac{b}{x}-\dfrac{x}{b}\right)=\dfrac{2}{b} $
Resolver los siguientes sistemas de ecuaciones
1. $\begin{array}{rcl|} x+3y \amp = \amp 4 \\ 2x+7y \amp = \amp 15 \\ \hline \end{array} $
2. $\begin{array}{rcl|} 2x+3z \amp = \amp 4 \\ 2x-6y+7z \amp = \amp 15 \\ x-2y+5z \amp = \amp 10 \\ \hline \end{array} $
3. $\begin{array}{rcl|} x+4y+3z \amp = \amp 1 \\ 2x+5y+4z \amp = \amp 4 \\ x-3y-2z \amp = \amp 5 \\ \hline \end{array} $
4. $\begin{array}{rcl|} 4x+y-2z \amp = \amp 0 \\ x-2y+z \amp = \amp 0 \\ 11x-4y+-z \amp = \amp 0 \\ \hline \end{array} $
5. $\begin{array}{rcl|} x^2+y^2 \amp = \amp 4 \\ 3x+4y \amp = \amp 9 \\ \hline \end{array} $
6. $\begin{array}{rcl|} x^2+xy+y^2 \amp = \amp 13 \\ x+y \amp = \amp 4 \\ \hline \end{array} $
7. $\begin{array}{rcl|} \dfrac{x}{y}+ \dfrac{y}{x} \amp = \amp \dfrac{25}{12} \\ x^2-y^2 \amp = \amp 7 \\ \hline \end{array}$
8. $\begin{array}{rcl|} x^2+y^2+2x \amp = \amp 13 \\ 3x+2y^2 \amp = \amp 4 \\ \hline \end{array} $
9. $\begin{array}{rcl|} x \amp = \amp 2wx \\ y \amp = \amp 4wy \\ z \amp = \amp wz \\ 2x^2+4y^2+z^2 \amp = \amp 8 \\ \hline \end{array} $
10. $\begin{array}{rcl|} 2x-wy \amp = \amp 0 \\ 2y-wx \amp = \amp 0 \\ z+wz \amp = \amp 0 \\ z^2+xy-4 \amp = \amp 0 \\ \hline \end{array} $
11. $\begin{array}{rcl|} 2(y+z)+wyz \amp = \amp 0 \\ 2(x+z)+wxz \amp = \amp 0 \\ 2(y+x)+wyx \amp = \amp 0 \\ xyz \amp = \amp 64 \\ \hline \end{array} $
12. $\begin{array}{rcl|} x+w(x-3) \amp = \amp 0 \\ y+w(y-4) \amp = \amp 0 \\ z \amp = \amp wz \\ (x-3)^2+(y-4)^2 \amp = \amp z^2 \\ \hline \end{array} $
13. $\begin{array}{rcl|} yz \amp = \amp w(y+z) \\ xz \amp = \amp w(x+z) \\ xy \amp = \amp w(y+x) \\ xy+xz+yz \amp = \amp 5 \\ \hline \end{array} $
Considere la igualdad

\begin{equation*} \dfrac{1}{\sqrt{1+x}}- \dfrac{1}{\sqrt{1-x}}=0 \end{equation*}
1. Determine para que valores de $x\in \mathbb{R}$ está definida.
2. Encuentre todos los $x\in \mathbb{R}$ que la satisfacen.
Determine el valor de verdad de las siguientes proposiciones:
1. $(\forall a\in \mathbb{R}^+)\left(\sqrt{a}+ \dfrac{1}{\sqrt{a}} \gt \dfrac{1}{2}\right)$
2. $(\forall a,b\in \mathbb{R})\left( a^2+b^2 \geq 2ab \right)$
3. $(\forall a\in \mathbb{R}) \left(0\leq a \Rightarrow \left(\frac{a}{a+1}\right)^2 \leq a \right)$
4. $(\forall a,b\in \mathbb{R}^+)\left( \dfrac{1}{a}+ \dfrac{1}{b}\geq \dfrac{4}{a+b}\right)$
5. $(\forall a,b\in \mathbb{R}^-)(a \lt b \Rightarrow a^2 \gt b^2)$
6. $(\forall x\in \mathbb{R})( \forall y\in \mathbb{R}-\{0\})\left(x \lt y \Rightarrow \dfrac{x}{y} \lt 1\right)$
7. $(\forall x\in \mathbb{R})(\forall y\in \mathbb{R}^+)(x\leq y \Rightarrow x\leq 2y)$
8. $(\forall x\in \mathbb{R})(\forall y\in \mathbb{R}^+)(x\leq y \Rightarrow y^{-1}\leq x^{-1})$
9. $(\forall x\in \mathbb{R})(\forall y\in \mathbb{R})(x+y= 1 \Rightarrow xy\leq \frac{1}{4})$
10. $(\forall x\in \mathbb{R})(\forall y\in \mathbb{R})(0\leq x\leq y \Rightarrow \frac{x}{y+1}\leq \frac{x}{y}\leq \frac{x+1}{y+1} )$
11. $(\forall x,y\in \mathbb{R})(|y-x|=|y+x|) \Rightarrow (x=0 \vee y=0)$
12. $(\forall x\in \mathbb{R})(\forall y\in \mathbb{R})(2x+4y=1 \Rightarrow x^2+y^2\geq \frac{1}{20})$
13. $(\forall x\in \mathbb{R})(\forall y\in \mathbb{R})((2\leq x\leq 3 \wedge 1\leq y\leq 2 ) \Rightarrow 1\leq \frac{x}{y} \leq 3)$
14. $(\forall x,y\in \mathbb{R})x^3+y^3\geq x^2-xy+y^2$
15. $(\forall a,b\in \mathbb{R}^+,a\neq b, n\in \mathbb{N})\left(\sqrt[n+1]{ab^n}\leq \dfrac{a+nb}{n}\right)$
16. $(\forall x,y,z\in \mathbb{R})(|x+y+z|\leq |x|+|y|+|z|)$
Considere en $\mathbb{R}$ la ecuación $m+\sqrt{x}=x\text{,}$ con $m\in \mathbb{R}\text{.}$
1. Determine todos los valores de $m\in \mathbb{R}$ para los cuales la ecuación tiene solución.
2. Encuentre la solución para $m=- \dfrac{1}{8}$
Determine en los siguientes casos condiciones sobre el parámetro $\lambda \in \mathbb{R}$ de modo que las ecuaciones
1. $x^2+\lambda x+3=0$
2. $x^2-2(\lambda+1)x+3=0$
3. $x^2+2(\lambda+1)x+3\lambda=0$
4. $\lambda x^2-2x+3\lambda=0$
tengan
1. Soluciones reales y distintas.
2. Soluciones reales e iguales.
3. No tengan solución.
Simplificar al máximo las siguientes expresiones
1. $\frac{a^2}{b}-\frac{a^2-b^2}{a+b}:\frac{a-b}{b} + \frac{b}{a}$
2. $\dfrac{1}{a+2-\frac{a+1}{a-\frac{1}{a}}} $
3. $(a^2-b^2):\left[\left( \dfrac{a^2+ab}{b^2+ab}\right): \left( \dfrac{a^2-ab}{b^2-ab}\right)\right]$
4. $\left( \dfrac{x^2-y^2}{x^3-y^3}\right)\left( \dfrac{x^2+xy+y^2}{x^2+2xy+y^2}\right)$
5. $\dfrac{\left(\frac{1}{a}+\frac{a^2}{b^3}\right) :\left(\frac{1}{a}-\frac{1}{b}+\frac{a}{b^2}\right)}{ \left(\frac{a+2b}{a+b}+\frac{a}{b}\right) :\left(\frac{a+2b}{a}-\frac{a}{a+b}\right)}$
6. $\left( \dfrac{ \dfrac{a+b}{2}-a}{ \dfrac{a+b}{2}-b}\right)^3- \dfrac{ \dfrac{a+b}{2}-2a+b}{ \dfrac{a+b}{2}+a-2b}$
7. $\dfrac{ \dfrac{1}{x}+ \dfrac{x}{x+1}}{x^3-1}- \dfrac{ \dfrac{x^2+1}{x^4-x^3}- \dfrac{1}{x^3-x^2}}{x^3+1}$
8. $\dfrac{\left(\frac{x(x+y)+y(y-x)}{y^2-x^2}\right) \left(\frac{(x+2y)x+y^2}{xy}\right)}{ \frac{y^2+x(x+2y)}{y(x+2y)}}$
9. $\dfrac{3x+2}{\sqrt[3]{2x+3}-\sqrt[3]{1-x}}$
10. $\dfrac{x-1}{\sqrt{x^2+x+2}-\sqrt{x+3}}$
11. $\dfrac{\sqrt{x+y}-\sqrt{x-y}}{\sqrt{x+y}+\sqrt{x-y}}$
12. $\dfrac{\sqrt[3]{8x^3+3x-1}-6x}{3x-\sqrt{x^2+x+1}}$
13. $\dfrac{x}{\sqrt{x+\sqrt{x-\sqrt{x}}}}$
14. $\dfrac{x}{\sqrt[n]{x^m}+\sqrt[m]{a^n}}\text{,}$ $n,m$ pares.
15. $\dfrac{\sqrt{\sqrt{x}-1}\cdot \sqrt{x+2\sqrt{x}+1}}{\sqrt{x-1}}$
Problemas de planteo
1. Si $a:b=2:3$ y $x= \dfrac{3a^2-2b+b^2}{3a+2b}\text{,}$ expresar $a$ en tanto $\%$ de $x\text{.}$
2. Para la altura del centro de gravedad de un tronco de cono rige la fórmula siguiente:
  
  \begin{equation*} X= \dfrac{R^2+2Rr+3r}{4(R^2+Rr+r^2)}\cdot b \end{equation*}
  
  ¿Qué tanto $\%$ de $b$ mide $X\text{,}$ si $r$ mide $50 \%$ de $R$ ?.
3. En un triángulo rectángulo se sabe que el cateto mayor mide $96\%$ de la hipotenusa. ¿Qué tanto $\%$ de la hipotenusa mide el cateto menor?.
4. La ley de Newton nos da $F=m\cdot a\text{.}$ ¿Qué tanto $\%$ aumenta la aceleración $a\text{,}$ si la fuerza $F$ aumenta en $42\%$ y la masa disminuye en $4\%$ ?.
5. Las áreas $A$ y $B$ de la figura (\ref{jojo}) están en la razón $2:3\text{.}$ Expresar $r$ en tanto $\%$ de $R\text{.}$
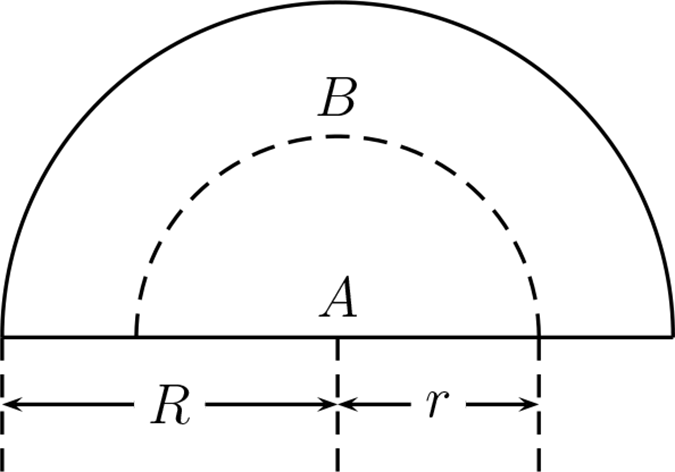
6. ¿En qué tanto $\%$ hay que aumentar el radio de una esfera para que su volumen aumente en $33.1\%$ ?.
7. Los diámetros de dos cilindros son entre si como $3:4$ y sus alturas como $5:6\text{.}$ ¿Qué tanto $\%$ del volumen del mayor mide el volumen del menor?.
8. Determinar dos números enteros consecutivos cuya suma de cuadrados se $128.525\text{.}$
9. Si $A$ hace un trabajo en tres horas y $B$ lo hace en cinco horas. ¿Cuánto tiempo demoran en hacer el trabajo ambos juntos?.
10. Hallar tres números consecutivos tales que si el menor se divide entre $20\text{,}$ el mediano entre $27$ y el mayor entre $41\text{,}$ la suma de los cocientes es $9\text{.}$
11. $A$ tiene el doble de dinero que $B\text{.}$ Si $A$ le da a $B$ $34$ pesos. $A$ tendrá los $5/11$ de lo que tenga $B\text{.}$ ¿Cuánto dinero tiene cada uno?.
12. Dos trabajadores uno de los cuales empieza a trabajar uno y medio días después que el otro, pueden completar un trabajo en $7$ días. Si cada uno de ellos hiciera el trabajo individualmente, el primero habría necesitado $3$ días más que el segundo que empezó después. ¿Cuántos días tardará cada obrero en realizar el trabajo individualmente?.
13. Un ingeniero contrata a un técnico para una cierta labor. Para esto le ofrece un sueldo anual de $\$ 500.000$ y un lingote de oro. Al cabo de siete meses el técnico termina su trabajo, por lo que recibe $\$250.000$ y el lingote de oro. ¿Cuál es el valor del lingote?.
14. Un cierto número de estudiantes deben acomodarse en una residencial. Si se ubicaran dos estudiantes por habitación entonces quedarían dos estudiantes sin pieza. Si se ubicaran tres estudiantes por habitación entonces sobrarían dos piezas. ¿Cuántas habitaciones disponibles hay en la residencial y cuántos estudiantes deben acodarse en ella?.
15. Cuando el precio de una marca popular de artículos de video es $\$ 300$ por unidad, una tienda vende $15$ unidades a la semana. Sin embargo cada vez que el precio se reduce en $\$10$ las ventas aumentan en $2$ unidades a la semana. ¿Qué precio de venta debe ponerse para obtener ingresos semanales de $\$ 7.000$ ?.
16. El cuerpo de la figura (\ref{jiji}) está formado por una semiesfera, un cilindro y un cono. Calcular $x\text{,}$ si el volumen total mide $112,5\pi [cm^3].$
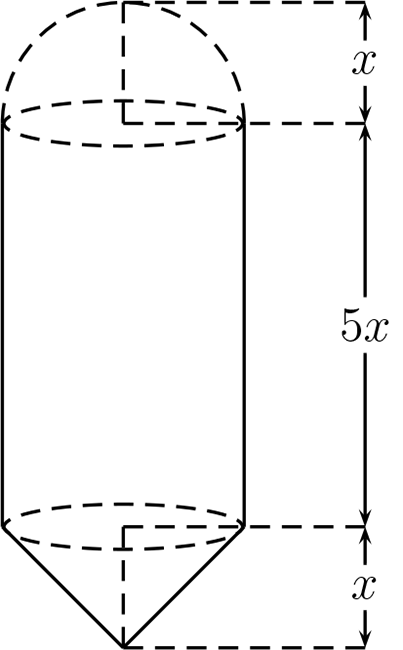
17. Un estanque con cierta cantidad de agua tiene forma de cono invertido. Al agregarle $10$ litros, como muestra la figura (\ref{juju}), el nivel de agua sube en un $20\%\text{.}$ Si la base del cono fuese reducida en un $40\%\text{,}$ manteniendo la misma altura resultaría un cono que estaría lleno con la cantidad de agua inicial.
  
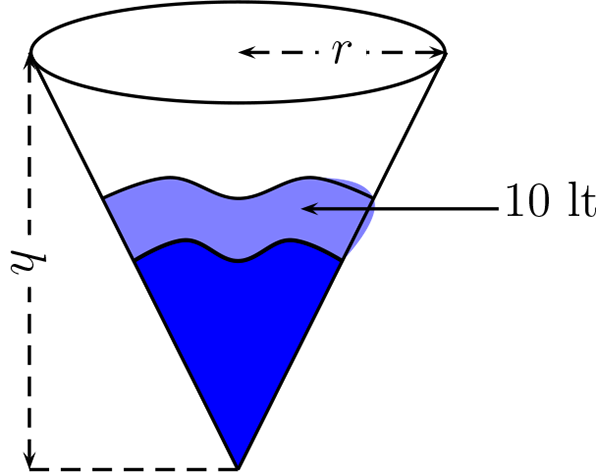
  Sabiendo que la altura del estanque es $50$ cm. Calcular el radio inicial y el volumen de agua contenido en un comienzo.
Resolver las siguientes inecuaciones
1. $\dfrac{x-1}{1-x}\leq 2x$
2. $(x+2)(x+1)\leq 0$
3. $\dfrac{x+3}{x}\leq 2$
4. $\dfrac{2}{x+2}+ \dfrac{x}{x+3}\leq 0$
5. $x- \dfrac{2x-3}{x}\geq 1-3x$
6. $\dfrac{34}{x-4}\leq \dfrac{2}{x-1}-5$
7. $\dfrac{x-2}{x+2}\geq \dfrac{x}{x+3}- \dfrac{x-1}{x^2-4}$
8. $\dfrac{13-5x}{x^2+x+1}\leq \dfrac{2}{x-2}$
Resolver las siguientes inecuaciones
1. $\dfrac{2(3|x+26|)}{155(x+6)} \lt \dfrac{533}{155(5x-1)}$
2. $\sqrt{-4x^2+25}\leq 3$
3. $\dfrac{\sqrt{2x-1}(x+1)}{(x^2+1)(x-2)}\geq 0$
4. $\sqrt{\sqrt{1-x}+1}\leq x-1$
5. $\sqrt{2-x}-2\sqrt{x}\leq \sqrt{x-2}$
6. $\sqrt{x-2}+3\sqrt{3x+1}\leq \sqrt{5x-2}$
7. $\sqrt{1-|x|} \gt 1-3x$
8. $\dfrac{x^2+2x+24}{\sqrt{2x+1}(x^2+x+5)}\geq 0$
9. $1-\left| \dfrac{1}{x}\right|\geq x$
10. $\sqrt{2-|x^2-x|}\leq \sqrt{3}$
11. $\dfrac{x}{|x+2|}\leq \dfrac{2}{x(x+2)}$
12. $|2-|x-1||\leq 1$
13. $\left|x+ \dfrac{1}{x}\right|\geq |x-3|$
14. $\dfrac{||x+3|-2|}{||x|-1|}\geq 2$
15. $|x+1|+||x-1|+3|\leq |x+2|+8$
16. $\left|1- \dfrac{1}{\sqrt{1-x}}\right|\geq 1$
17. $\dfrac{|x-1|-|x+1|}{|x^2-1|}\leq \dfrac{|x-1|}{x+1}$
18. $\dfrac{|x-1|(\sqrt{x+3}+|x|)}{|x+3|-|x-4|}\geq 0$
19. $3x +1 +|x-1| \lt \sqrt{x}$
Axioma del Supremo
1. Determine el supremo y el ínfimo de los siguientes conjuntos
  1. $A=[-2,3[\cup]5,\sqrt{42}[$
  2. $A=]-3,0[\cup]\sqrt{4},6]$
  3. $A=\{x\in \mathbb{R}\,\,|\,\,|x|\leq 5 \}$
  4. $A=\{x\in \mathbb{R}\ | \ x^2-3x+2\leq 0\}$
  5. $A=\left\{x\in \mathbb{R}\ |\ \sqrt{|x|+1} \lt 2 \right\}$
  6. $A=\left\{x\in \mathbb{R}\ |\ \frac{1}{x+1} \lt 2 \right\}$
  7. $A=\left\{x\in \mathbb{R}\ |\ \dfrac{x}{2}\leq |x-1|\leq \dfrac{9}{2} \right\}$
2. Sean
  1. $A=\{x\in \mathbb{R}\,\,|\,\,x^2-7 \lt 1 \}$ y $B=\{x\in \mathbb{R}\,\,|\,\,x^2-2x-3\leq 0\}$
  2. $A=\{x\in \mathbb{R}\,\,|\,\,|x|\leq 3 \}$ y $B=\left\{x\in \mathbb{R}\,\,\left|\,\,0 \lt \dfrac{-1-x(x+1)}{x+1}\right.\right\}$
  Encuentre en cada caso (si existen) el Supremo e ínfimo correspondientes a los conjuntos $A, B, A\cup B$ y $A\cap B\text{.}$
3. Sea $\alpha \in \mathbb{R}$ y $A\subset \mathbb{R}$ acotado. Se define
  
  \begin{equation*} \begin{array}{rcl} \alpha +A\amp =\amp \{\alpha +a\,\,|\,\,a\in A \}. \\ \alpha \cdot A\amp =\amp \{\alpha a\,\,|\,\,a\in A \}. \end{array} \end{equation*}
  
  Demuestre que
  1. $\alpha +\sup(A)=\sup(\alpha +A)$
  2. $\alpha +\inf(A)=\inf(\alpha +A)$
  3. Si $\alpha$ es positivo, entonces $\sup(\alpha A)=\alpha \sup(A) $
  4. Si $\alpha$ es positivo, entonces $\inf(\alpha A)= \alpha \inf(A)$
  5. Si $\alpha$ es negativo, entonces $\sup(\alpha A)=\alpha \inf(A)$
  6. Si $\alpha$ es negativo, entonces $\inf(\alpha A)=\alpha \sup(A)$
4. Sean $A,B$ dos subconjuntos acotados de $\mathbb{R}$ y
  
  \begin{equation*} A+B=\{a+b\,\,|\,\,a\in A \wedge b\in B\}. \end{equation*}
  
  Demuestre que:
  1. $\sup(A+B)=\sup(A)+\sup(B)$
  2. $\inf(A+B)=\inf(A)+\inf(B)$
5. Demuestre que si
  
  \begin{equation*} A=\left\{x_n\in \mathbb{R}\,\,\left|\,\,x_n= \dfrac{2n}{n+3},\ n\in \mathbb{N}\right.\right\} \end{equation*}
  
  entonces el $\sup(A)=2$ .
6. Demuestre que si
  
  \begin{equation*} A=\left\{x_n\in \mathbb{R}\,\,\left|\,\,x_n= \dfrac{2}{3n+1}, n\in \mathbb{N}\right.\right\} \end{equation*}
  
  entonces el $\inf(A)=0$ .
7. Determine y demuestre si existe el supremo y el ínfimo de
  
  \begin{equation*} A=\left\{x_n\in \mathbb{R}\,\,\left|\,\,x_n= \dfrac{2}{n+3}, n\in \mathbb{N}\right.\right\}. \end{equation*}
8. Determine y demuestre si existe el supremo y el ínfimo de
  
  \begin{equation*} A=\left\{x_n\in \mathbb{R}\,\,\left|\,\,x_n=(-1)^n \dfrac{5}{2n+3}, n\in \mathbb{N}\right.\right\}. \end{equation*}