Definición 3.2.1
Se dice que \(f\) es una función de números reales si y sólo si
\(f\) una relación en los números reales y
\((\forall x,y,z \in \mathbb{R})((x,y),(x,z)\in f \Rightarrow y=z)\)
Sección 3.2 Función
¶Una función \(f\) es una relación de \(A\) en \(B\) tal que a cada elemento del dominio de la relación, le corresponde un único elemento del recorrido de la relación.
Observación: En general, se dice que \(f \) es una función de \(A\) en \(B\) si y sólo si \(f\) es una relación entre \(A\) y \(B\) y \((\forall x\in A)(\exists ! y\in B)(x f y)\text{.}\)
Es decir, no es función cuando un el elemento tiene más de una imagen en el conjunto de llegada. Podemos graficar esta situación, donde \(f \) no es función, con el siguiente diagrama
En cambio el siguiente diagrama, representa una función.
Ejemplo 3.2.2
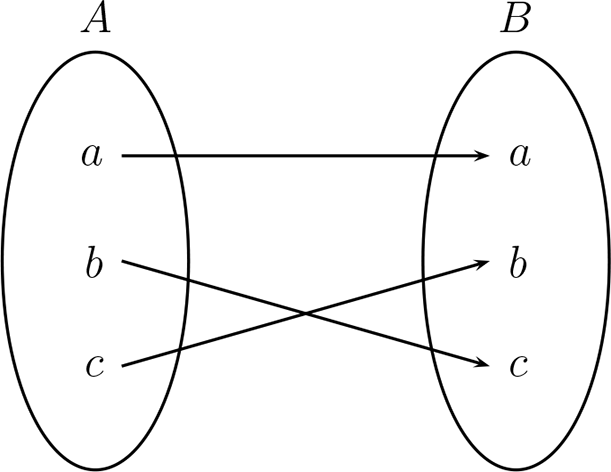
Determinar si la siguiente relación es una función
\begin{equation*}
\mathcal{L}=\{
(x,y)\in \mathbb{R}^2\ | \ 2x+3y=1 \}.
\end{equation*}
Sean \(a,b,c \in \mathbb{R}\) tales que \((a,b),(a,c)\in \mathcal{L}\)
Luego tenemos que
\begin{equation*}
2a+3b=1 \ \ \wedge \ \ 2a+3c=1
\end{equation*}
Reemplazando tenemos
\begin{equation*}
\begin{array}{rcl}
2a+3b\amp =\amp 2a+3c \\
3b\amp =\amp 3c\\
b\amp =\amp c
\end{array}
\end{equation*}
Luego \(\mathcal{L}\) es función.
Ejemplo 3.2.3
Determinar si la siguiente relación es una función
\begin{equation*}
\mathcal{P}=\{ (x,y)\in \mathbb{R}^2\ | \ y^2=4x+1 \}
\end{equation*}
Sean \(a,b,c \in \mathbb{R}\) tales que \((a,b),(a,c)\in \mathcal{P}\text{.}\) Luego tenemos que
\begin{equation*}
b^2=4a+1 \ \ \wedge \ \ c^2=4a+1
\end{equation*}
Reemplazando tenemos
\begin{equation*}
b^2=c^2
\end{equation*}
\begin{equation*}
b=c \ \ \vee \ \ b=-c
\end{equation*}
podemos considerar los pares ordenados \((1,5)\) y \((1,-5)\) ambos puntos pertenece a \(\mathcal{P}\) pero \(5\neq -5\text{,}\) luego \(\mathcal{P}\) no es una función.
Ejemplo 3.2.4
Determinar si la siguiente relación es una función
\begin{equation*}
\mathcal{H}=\{ (x,y)\in \mathbb{R}^2\ | \ y^2-3x^2=1 \wedge y \lt 0 \wedge x\geq 0 \}
\end{equation*}
Sean \(a,b,c \in \mathbb{R}\) tales que \((a,b),(a,c)\in \mathcal{H}\text{.}\) Luego tenemos que \(a \in \mathbb{R}^+_0,b,c \in \mathbb{R}^-\) además
\begin{equation*}
b^2-3a^2=1 \ \ \wedge \ \ c^2-3a^2=1
\end{equation*}
Reemplazando tenemos
\begin{equation*}
b^2-3a^2=c^2-3a^2
\end{equation*}
\begin{equation*}
b^2=c^2
\end{equation*}
\begin{equation*}
b=c \ \ \vee \ \ b=-c
\end{equation*}
pero \(b \lt 0\) y \(c \lt 0\text{,}\) luego es imposible que \(b=-c\) por lo tanto tenemos que
\begin{equation*}
b=c.
\end{equation*}
Así \(\mathcal{H}\) es una función.
[inlineexercise] 3.2.5
Determine si los siguientes conjunto son funciones
- \(F=\{ (x,y)\in \mathbb{R}\times \mathbb{R}\ | \ y=3x+2\ \}\)
- \(F=\{ (x,y)\in \mathbb{R}\times \mathbb{R}\ | \ x^2+y^2=4\ \} \)
- \(F=\{ (x,y)\in \mathbb{R}\times \mathbb{R}\ | \ (x-1)^2+(y-3)^2=4 \wedge y \geq 3 \ \}\)
- \(F=\{ (x,y)\in \mathbb{R}\times \mathbb{R}\ | \ \dfrac{(x+1)^2}{4}+\dfrac{(y-1)^2}{9}=1 \ \}\)
- \(F=\{ (x,y)\in \mathbb{R}\times \mathbb{R}\ | \ \dfrac{(x+1)^2}{4}+\dfrac{(y-1)^2}{9}=1 \wedge y \leq 1 \ \}\)
Observación: Tenga presente que una función es un conjunto, luego la igual de funciones es una igual de conjuntos.
Subsección 3.2.1 Dominio y Recorrido
¶Definición 3.2.6 Dominio y Recorrido de una Función
Sea \(f\) una función real.
Se define el Dominio de \(f\) igual a
\begin{equation*}
Dom(f)=\{x\in \mathbb{R}\ \ | \
\ (\exists y\in \mathbb{R} )((x, y)\in f) \}.
\end{equation*}
Se define el Recorrido de \(f\) igual a
\begin{equation*}
Rec(f)=\{y\in\mathbb{R}\ \ | \ \ (\exists x\in \mathbb{R})((x,y)\in f )\}
\end{equation*}
A continuación revisaremos los ejemplos anteriores.
Ejemplo 3.2.7
Determinar dominio y recorrido de
\begin{equation*}
\mathcal{L}=\{
(x,y)\in \mathbb{R}^2\ | \ 2x+3y=1 \}.
\end{equation*}
Sea \(x\in Dom(\mathcal{L})\text{,}\) luego existe \(y\in\mathbb{R}\) tales que \((x,y)\in \mathcal{L}\text{,}\) es decir,
\begin{equation*}
2x+3y=1.
\end{equation*}
Despejando obtenemos que
\begin{equation*}
y=\frac{1-2x}{3}.
\end{equation*}
De lo anterior tenemos que:
Dado \(x \in \mathbb{R}\text{,}\) existe \(y=\frac{1-2x}{3} \in \mathbb{R}\) tal que
\begin{equation*}
2(x)+3\frac{1-2x}{3}=1,
\end{equation*}
de lo cual, \((x,\frac{1-2x}{3})\in \mathcal{L}\text{.}\)
Luego
\begin{equation*}
Dom (\mathcal{L}) = \mathbb{R}
\end{equation*}
Para el recorrido tenemos que un desarrollo similar, dado por \(y \in \mathbb{R}\text{,}\) luego \(x=\frac{1-3y}{2}\) el cual es un número real, por lo tanto tenemos que el recorrido es:
\begin{equation*}
Rec (\mathcal{L}) =
\mathbb{R}
\end{equation*}
Ejemplo 3.2.8
Determinar dominio y recorrido de la siguiente función
\begin{equation*}
f=\{ (x,y)\in \mathbb{R}^2\ | \ y^2-3x^2=1 \wedge y \lt 0 \wedge x\geq 0 \}
\end{equation*}
Sea \(x\in Dom(f)\subseteq \mathbb{R}^+_0\text{,}\) luego existe \(y\in\mathbb{R}^-\) tales que \((x,y)\in f\text{,}\) es decir,
\begin{equation*}
y^2-3x^2=1.
\end{equation*}
Despejando obtenemos que
\begin{equation*}
\begin{array}{rcl}
y^2\amp =\amp 1+3x^2.\\
y^2\amp =\amp 1+3x^2.\\
|y|\amp =\amp \sqrt{1+3x^2} \\
y\amp =\amp - \sqrt{1+3x^2}, \ \ \ y \lt 0
\end{array}
\end{equation*}
De lo anterior tenemos que:
Dado \(x \in \mathbb{R}^+_0\) existe \(y=- \sqrt{1+3x^2} \in \mathbb{R}^-\) tal que
\begin{equation*}
(- \sqrt{1+3x^2})^2-3(x)^2=1,
\end{equation*}
es decir, \((x,- \sqrt{1+3x^2})\in f.\)
Luego
\begin{equation*}
Dom (f) = \mathbb{R}^+_0
\end{equation*}
Para el recorrido tenemos que un desarrollo similar, dado por \(y \in \mathbb{R}\text{,}\)
\begin{equation*}
\begin{array}{rcl}
y^2-3x^2\amp =\amp 1\\
3x^2 \amp =\amp y^2-1\ \ (*)\\
|x|\amp =\amp \sqrt{\frac{y^2-1}{3}} \\
x\amp =\amp \sqrt{\frac{y^2-1}{3}}, \ \ \ x\geq 0
\end{array}
\end{equation*}
luego la restricción \((*)\) esta dada por \(y^2-1\geq 0\text{,}\) por lo tanto \(|y|\geq 1 \) con lo cual \(y \leq -1\text{.}\) De este modo \(x=\sqrt{\frac{y^2-1}{3}}\) es un número real y por lo tanto tenemos que el recorrido es:
\begin{equation*}
Rec (f) = ]\infty, -1]
\end{equation*}
Ejemplo 3.2.9
Dada la relación \(f =\{(x,y)\in \mathbb{R}\times\mathbb{R} \mid y(x-4)=2x+5\}\subseteq \mathbb{R}\times\mathbb{R}\text{.}\)
Determine el dominio y el recorrido de la función.
Sean \(x,y\in \mathbb{R}\text{,}\) tales que \((x,y)\in f\text{,}\) por lo tanto tenemos
\begin{equation*}
y(x-4)=2x+5
\end{equation*}
Cuando \(x \neq 4\) tenemos que existe un único valor de \(y=\frac{2x+5}{x-4}\)
Para \(x=4\text{,}\) reemplazando y tenemos que \(0=13\text{,}\) lo que es una contradicción, luego el dominio de \(f\) es \(Dom(f)=\mathbb{R} -\{4\}\)
Sea \(y\in Rec (f)\text{,}\) luego existe \(x\in \mathbb{R}-\{4\}\) tal que \((x,y)\in f\text{,}\)
\begin{equation*}
\begin{array}{rcc}
y(x-4) = \amp 2x+5 \amp \\
yx - 4y = \amp 2x+5 \amp \\
yx - 2x = \amp 5+4y \amp \\
x(y-2) = \amp 5+4y \amp
\end{array}
\end{equation*}
Para \(y=2\text{,}\) reemplazamos obtenemos que \(0=13\text{,}\) lo es falso.
Por lo cual tenemos que \(y\neq 2\text{,}\) y por ende podemos despejar el valor de:
\begin{equation*}
x = \frac{5+4y}{y-2}.
\end{equation*}
Recordemos que \(x \in Dom(f)\text{,}\) para ello notemos lo siguiente
\begin{equation*}
\frac{5+4y}{y-2}= 4 \Leftrightarrow 5+4y = 4y -8 \Leftrightarrow 5 = -8
\end{equation*}
es decir,
\begin{equation*}
\frac{5+4y}{y-2}\neq 4 \Leftrightarrow 5 \neq -8
\end{equation*}
Luego el recorrido de la función es \(Rec (f)=\mathbb{R}-\{2\}\)
Ejemplo 3.2.10
Dada la función \(f =\{(x,y)\in \mathbb{R}^2 \mid y=\sqrt x \wedge x\geq 0 \}\subseteq \mathbb{R}^2.\)
Determine el dominio y el recorrido.
Ya que \(f =\{(x,y)\in \mathbb{R}^2\mid y=\sqrt x \wedge x\geq 0 \}\text{,}\)
Como la expresión \(y=\sqrt{x}\) está bien definida solamente cuando \(x\in \mathbb{R}^+_0.\)
Luego
\begin{equation*}
Dom (f)=\mathbb{R}^+_0.
\end{equation*}
Sea \(y\in Rec(f)\text{,}\) luego existe \(x \in Dom(f)= \mathbb{R}^+_0\text{,}\) tal que \((x,y) \in f\text{.}\)
\begin{equation*}
\begin{array}{rcl}
y \amp =\amp \sqrt{x} \\
y^2 \amp =\amp x \mbox{ con } x \in \mathbb{R}^+_0
\end{array}
\end{equation*}
sabemos que \(y^2 \geq 0\) es siempre verdadero.
Por lo tanto el recorrido de \(f\) es \(Rec(f)=\mathbb{R}_0^+\)
Ejemplo 3.2.11
Dada la relación \(f =\{(x,y)\in A\times \mathbb{R} \mid y(x-1)=x^2-1\}\)
Para \(A=\mathbb{R}\text{,}\) determine si \(f\) es una función.
Determine \(A \subseteq \mathbb{R}\) maximal, tal que \(f\) es función, además su \(Dom(f)\) y \(Rec(f)\)
Veremos si es función.
Si \(x\neq 1\text{,}\) tenemos que \(y= \frac{x^2-1}{x-1}=x+1\text{,}\) luego el valor de \(y\) es único.
Si \(x=1\text{,}\) se tiene que \(0=0\text{,}\) luego todo los valores de \(y\) satisfacen, de otro modo \((1,y) \in f\text{,}\) para todo \(y \in \mathbb{R}\text{,}\) por ende no es función.
El conjunto maximal tal que \(f\) es función esta dado por \(A = \mathbb{R}-\{1\}\text{,}\) y en este caso el dominio es \(Dom(f)= \mathbb{R}-\{1\}\)
Para determinar el recorrido, sea \(y\in Rec(f)\text{,}\) con \(x\in \mathbb{R}-\{1\}\text{,}\) tal que \((x,y) \in f\text{,}\) luego tenemos que
\begin{equation*}
\begin{array}{lrl}
\amp y = \amp \frac{x^2-1}{x-1} \\
\amp y = \amp (x+1) \\
\amp y -1 = \amp x
\end{array}
\end{equation*}
Falta analizar que \(y-1=x \neq 1\text{,}\) es decir,
\begin{equation*}
y-1 = 1 \Leftrightarrow y= 2
\end{equation*}
de otro modo
\begin{equation*}
y-1 \neq 1 \Leftrightarrow y\neq 2
\end{equation*}
Por lo tanto el recorrido de la función es: \(\mathbb{R}-\{2\}.\)
Subsección 3.2.2 Notación Funcional
¶Sea \(f\) una función de números real, luego existe el Dominio de \(f\) y el Recorrido de \(f\text{,}\) además a cada \(x\in Dom(f)\) existe un único elemento \(y\) en el recorrido, el cual denotamos por \(y=f(x)\text{.}\) Luego la función, la podemos codificar del siguiente modo:
\begin{equation*}
\begin{array}{rccl}
f:\amp Domf \amp \longrightarrow \amp B \\
\amp \text{ variable }\amp \longmapsto \amp \text{único valor asociada }
\end{array}
\end{equation*}
Donde \(B\) es llamado ''Conjunto de llegada'' y es un subconjunto de los Número Reales que contiene al recorrido, de otro modo \(Rec(f) \subseteq B \subseteq \mathbb{R}\text{,}\) la variable habitualmente empleada es \(x\text{,}\) por último note que el valor asociado debe pertenecer a \(B\text{.}\)
En los ejemplos usaremos los ejercicios anteriores.
En el primer ejemplo tenemos que
\begin{equation*}
\mathcal{L}=\{ (x,y)\in \mathbb{R}^2\ | \ 2x+3y=1 \}.
\end{equation*}
podemos escribirlo usando la notación:
\begin{equation*}
\begin{array}{cccc}
\mathcal{L}: \amp \mathbb{R} \amp \longrightarrow \amp \mathbb{R} \\
\amp x \amp \longmapsto \amp \frac{1-2x}{3}
\end{array}
\end{equation*}
En el siguiente ejemplo tenemos que
\begin{equation*}
f=\{(x,y)\in \mathbb{R}^2\ |\ y^2-3x^2=1\wedge y \lt 0\wedge x\geq 0\}
\end{equation*}
podemos escribirlo usando la notación:
\begin{equation*}
\begin{array}{cccc}
f: \amp \mathbb{R}^+_0 \amp \longrightarrow \amp ]-\infty, 0[ \\
\amp x \amp \longmapsto \amp -\sqrt{1+3x^2}
\end{array}
\end{equation*}
El el tercer ejemplo se tiene que
\begin{equation*}
f =\{(x,y)\in \mathbb{R}\times\mathbb{R} \mid y(x-4)=2x+5\}.
\end{equation*}
en forma abreviada tenemos:
\begin{equation*}
\begin{array}{cccc}
f: \amp \mathbb{R}-\{4\} \amp \longrightarrow \amp \mathbb{R}\\
\amp x \amp \longmapsto \amp \frac{2x+5}{x-4}
\end{array}
\end{equation*}
o bien
\begin{equation*}
\begin{array}{cccc}
f: \amp \mathbb{R}-\{4\} \amp \longrightarrow \amp \mathbb{R}-\{2\} \\
\amp x \amp \longmapsto \amp \frac{2x+5}{x-4} \\
\end{array}
\end{equation*}
En el cuarto ejemplo se tiene que
\begin{equation*}
f =\{(x,y)\in \mathbb{R}^2 \mid y=\sqrt x \wedge x\geq 0 \},
\end{equation*}
en forma abreviada tenemos:
\begin{equation*}
\begin{array}{cccc}
f: \amp \mathbb{R}^+_0 \amp \longrightarrow \amp \mathbb{R}^+_0\\
\amp x \amp \longmapsto \amp \sqrt{x}
\end{array}
\end{equation*}
En el último ejemplo se tiene que
\begin{equation*}
f =\{(x,y)\in \mathbb{R}^2 \mid y(x-1)=x^2-1, x\neq 1\},
\end{equation*}
en forma abreviada tenemos:
\begin{equation*}
\begin{array}{cccc}
f: \amp \mathbb{R}-\{1\} \amp \longrightarrow \amp \mathbb{R}-\{2\}\\
\amp x \amp \longmapsto \amp \frac{x^2-1}{x-1}
\end{array}
\end{equation*}
o bien
\begin{equation*}
\begin{array}{cccc}
f: \amp \mathbb{R}-\{1\} \amp \longrightarrow \amp \mathbb{R}-\{2\}\\
\amp x \amp \longmapsto \amp x+1
\end{array}
\end{equation*}
Observación: La igualdad de funciones corresponde solamente a una igualdad de conjuntos, pero ahora es importante, revisar esta noción de igualdad de funciones con esta nueva notación.
Definición 3.2.12
Dadas dos funciones \(f:A\longrightarrow B\) y \(g:C\longrightarrow D\) se dice que \(f=g\) si y sólo si se cumple que:
- \(A=C\)
- \((\forall x\in A)(f(x)=g(x))\)
o bien, dos funciones son iguales si tienen el mismo dominio, y para cada elemento del dominio tiene idénticas imágenes.
Ejemplo 3.2.13
Sean \(\begin{array}[t]{lccl} f: \amp \mathbb{R}\amp \longrightarrow \amp \mathbb{R}\\ \amp x \amp \longmapsto \amp x+1\\ \end{array}\) y \(\begin{array}[t]{lccl} g:\amp \mathbb{R}-\{0\}\amp \longrightarrow \amp \mathbb{R}\\ \amp x \amp \longmapsto \amp \frac{x^2 + x}{x} \\ \end{array}\)
En este caso tenemos que \(f\neq g\) ya que \(Dom(f)\neq Dom (g).\)
Subsección 3.2.3 Ejercicios Resueltos
¶Ejemplo 3.2.14
Sea \(\begin{array}[t]{rccl} f: \amp D \amp \longrightarrow \amp [1,9[ \\ \amp x \amp \longmapsto \amp f(x)=\sqrt{|x|-2}-1 \\ \end{array}\)
Determine el dominio de la función.
Para determinar el dominio de la función, primero debemos restringirla, es decir, determinar para qué valores de \(x\) la imagen son números reales.
\begin{equation*}
\begin{array}{rll}
|x|-2 \amp \geq \amp 0 /+2 \\
|x| \amp \geq \amp 2 \\
x\geq 2 \amp \vee \amp x \leq -2 \\
\end{array}
\end{equation*}
entonces
\begin{equation*}
x\in ]-\infty,-2]\cup [2, +\infty[
\end{equation*}
Como la función tiene como conjunto de llegada el intervalo \([1,9[\text{,}\) debemos encontrar los valores de \(x\) para los cuales la imagen está en este conjunto.
\begin{equation*}
\begin{array}{rcl}
y\in [1,9[ \amp \Leftrightarrow \amp 1\leq y \lt 9 \\
\sqrt{|x|-2}-1\in [1,9[ \amp \Leftrightarrow \amp 1\leq \sqrt{|x|-2}-1 \lt 9 /+1\\
\amp \Leftrightarrow \amp 2\leq\sqrt{|x|-2} \lt 10 / ( )^2 \\
\amp \Leftrightarrow \amp 4\leq |x|-2 \lt 100 / +2\\
\amp \Leftrightarrow \amp 6\leq |x| \lt 102
\end{array}
\end{equation*}
Luego tenemos
\begin{equation*}
\begin{array}{rcl}
6\leq |x| \amp \Leftrightarrow\amp x \leq -6 \vee 6 \leq x \\
|x| \lt 102 \amp \Leftrightarrow \amp -102 \lt x \wedge x \lt 102
\end{array}
\end{equation*}
De lo cual tenemos
\begin{equation*}
x\in ]-102,-6]\cup [6,102[.
\end{equation*}
Entonces el dominio de \(f\)
\begin{equation*}
Dom(f)=(]-\infty,-2]\cup[2,+\infty[)\cap(]-102,-6]\cup[6,102[)
\end{equation*}
Por lo tanto
\begin{equation*}
Dom(f)= ]-102,-6]\cup [6,102[.
\end{equation*}
Ejemplo 3.2.15
Sea \(\begin{array}[t]{rccc} f:\amp ]-\infty,-2[ \amp \longrightarrow \amp \mathbb{R}\\ \amp x\amp \longmapsto \amp \frac{1}{\sqrt{|x|-1}}+1. \end{array}\)
Determine el recorrido de \(f.\)
Sean \(x \in ]-\infty,-2[\) \(y \in Rec(f)\text{,}\) luego
\begin{equation*}
\begin{array}{rll}
y= \amp f(x)\\
y= \amp \frac{1}{\sqrt{|x|-1}}+1 \amp /-1\\
y-1 = \amp \frac{1}{\sqrt{|x|-1}} \amp /()^2 \text{, } y-1 \geq 0\\
(y-1)^2 = \amp \frac {1}{|x|-1} \amp \\
|x|-1 = \amp \frac{1}{(y-1)^2} \amp /+1 \text{, } y\neq 1\\
|x| = \amp \frac{1}{(y-1)^2} +1 \amp \\
\end{array}
\end{equation*}
Como \(x \in ]-\infty,-2[\text{,}\) tenemos que \(|x|=-x\) y nos queda
\begin{equation*}
\begin{array}{cll}
-x = \amp \frac{1}{(y-1)^2}+1 \amp /\cdot(-1) \\
x = \amp -1 -\frac{1}{(y-1)^2}\\
\end{array}
\end{equation*}
por otro lado tenemos que \(x\leq -2\text{,}\) entonces
\begin{equation*}
\begin{array}{cll}
-1 - \frac{-1}{(y-1)^2} \leq -2 \amp \Leftrightarrow \frac{-1}{(y-1)^2}\leq -1 \amp / \cdot(-1)\\
\amp \Leftrightarrow \frac{1}{(y-1)^2} \geq 1 \amp \\
\amp \Leftrightarrow 1 \geq (y-1)^2 \amp /\sqrt{}\\
\amp \Leftrightarrow 1\geq |y-1| \amp \\
\amp \Leftrightarrow -1\leq y-1 \leq 1 \amp \\
\amp \Leftrightarrow 0\leq y \leq 2 \amp
\end{array}
\end{equation*}
antes de concluir debemos considerar las anteriores restricciones, luego el recorrido de la función nos queda:
\begin{equation*}
Rec(f)=[0,2] \cap ]1,+\infty[ = ]1,2].
\end{equation*}
Ejemplo 3.2.16
Sea \(f(x)=1-x-x^2\) una función real.
Determine el dominio máximo y su recorrido de \(f\text{.}\)
Como la expresión \(f(x)=1-x-x^2\text{,}\) siempre esta bien definida o siempre podemos evaluar, luego \(Dom(f) =\mathbb{R}.\)
Ahora, para encontrar el recorrido de \(f\text{.}\) Sea \(x\in \mathbb{R}\text{,}\) tal que
\begin{equation*}
\begin{array}{rcl}
y\amp = \amp f(x) \\
y\amp = \amp 1-x-x^2 \\
x^2+x+(y-1)\amp = \amp 0
\end{array}
\end{equation*}
La cual es una ecuación de segundo grado, para determinar si existe \(x\) debemos calcular su discriminante es \(1-4(y-1) \geq 0\text{,}\) luego aplicando la formula de segundo grado tenemos
\begin{equation*}
x = \frac{-1\pm\sqrt{5-4y}}{2}
\end{equation*}
Entonces, la única restricción es el discriminante
\begin{equation*}
\begin{array}{rcl}
5-4y \amp \geq 0 \amp \\
\frac{5}{4} \amp \geq y \amp \\
\end{array}
\end{equation*}
Luego
\begin{equation*}
Rec(f)=]-\infty,\frac{5}{4}]
\end{equation*}
Ejemplo 3.2.17
Sea \(\begin{array}[t]{rccl} f:\amp A\subseteq\mathbb{R} \amp \longrightarrow \amp \mathbb{R}\\ \amp x\amp \longmapsto \amp \left \{ \begin{array}{rcc} 2+x \amp si \amp x\leq 1\\ x^2+1 \amp si \amp x \gt 1 \end{array} \right. \end{array}\)
Determinar \(A\) igual al dominio máximo y el recorrido de la función.
El dominio máximo de ésta función es \(\mathbb{R}.\)
Como \(f\) es una función definida en tramos, para determinar el recorrido consideraremos primero el tramo en que la función está definida para todos los \(x\leq 1\) y la llamaremos \(f_1\text{,}\) es decir
\begin{equation*}
\begin{array}{cccl}
f_1\amp ]-\infty,1] \amp \rightarrow \amp \mathbb{R} \\
\amp x\amp \mapsto \amp 2+x
\end{array}
\end{equation*}
Sea \(y \in \mathbb{R}\) tal que existe \(x \leq 1\text{,}\) tal que
\begin{equation*}
y= 2+x \Leftrightarrow y-2= x
\end{equation*}
como \(x\leq 1\text{,}\) luego
\begin{equation*}
y-2 \leq 1 \Leftrightarrow y \leq 3
\end{equation*}
Por lo tanto
\begin{equation*}
Rec(f_1)=]-\infty,3]
\end{equation*}
Ahora veremos que pasa con el recorrido cuando \(x \gt 1.\) Llamaremos \(f_2\) al segundo tramo de la función, es decir,
\begin{equation*}
\begin{array}{cccl}
f_2\amp ]1,\infty[ \amp \rightarrow \amp \mathbb{R} \\
\amp x\amp \mapsto \amp x^2+1
\end{array}
\end{equation*}
Sea \(y \in \mathbb{R}\) tal que existe \(x \gt 1\text{,}\) tal que
\begin{equation*}
y = x^2+1 \Leftrightarrow y-1= x^2,
\end{equation*}
de lo cual \(y-1 \geq 0\) y \(\sqrt{y-1}= |x|\text{,}\) pero \(x \gt 1\)
\begin{equation*}
\sqrt{y-1} \gt 1 \Leftrightarrow y-1 \gt 1
\end{equation*}
De este modo tenemos
\begin{equation*}
Rec(f_2)=]-\infty,2[
\end{equation*}
Finalmente el recorrido de la función \(f\) es
\begin{equation*}
Rec(f)=Rec(f_1)\cup Rec(f_2)=]-\infty,3]
\end{equation*}
Subsección 3.2.4 Representación Gráfica
¶La gráfica de una función \(f:A\longrightarrow B\text{,}\) se define como el conjunto de pares ordenados siguiente:
\begin{equation*}
Graf(f)=\{(x,f(x))\in A\times B\mid y=f(x),x\in A\}\subset\mathbb{R}^2
\end{equation*}
Note que hemos vuelto a la notación de relación de números reales.
La representación gráfica de \(f\text{,}\) se llama curva y se consigue marcando los puntos del conjunto en el producto cartesiano \(A\times B\) y en el caso real en el plano cartesiano.
De lo anterior, tenemos en el eje \(x\) los elementos del dominio y en el eje \(y\) los elementos del conjunto de llegada.
Observación: Se dice que \(x\) es un cero de \(f\text{,}\) si y sólo si \(f(x)=0\text{.}\) Geométricamente los ceros de una función son los puntos en que la gráfica intersecan o corta al eje \(x\text{.}\)
Ejemplo 3.2.18
En la función real \(f(x)=2x+2\text{,}\) se tiene que \(-1\) es un cero de \(f\) y por lo tanto el punto \((-1,0)\) pertenece a la intersección del gráfico de \(f\) con el eje \(x\text{.}\)
Ejemplo 3.2.19
Graficar la función \(f(x)=2x+5\text{.}\)
Para graficar la función podemos hacer una tabla, que contengan las variables independiente y dependiente, asignándole posibles valores a la variable independiente obtenemos los valores de la variable dependiente al reemplazar los valores dados y así podemos representar algunos puntos en el plano. Además conociendo que la curva, en este caso, se trata de una recta, luego nos bastan dos puntos, ellos pueden ser \((0,5),(1,7)\in f\text{.}\)
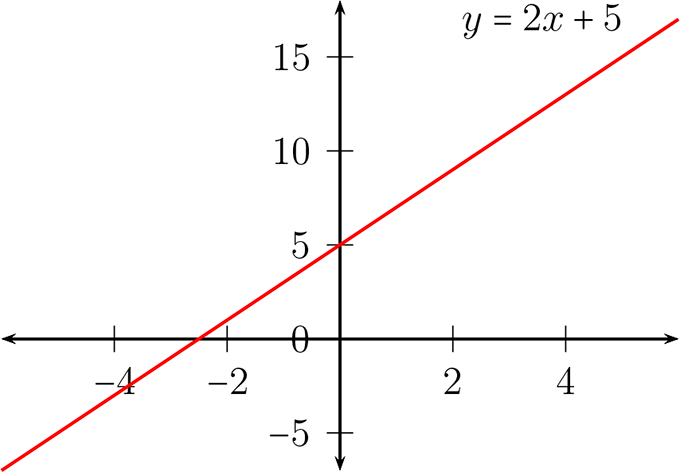
Observación: La gráfica de una función, nos ayuda a poder determinar el dominio y el recorrido de ella
Ejemplo 3.2.20
Graficar la función \(f(x)=x^2-5x+6\text{.}\)
Para graficar, usamos el hecho que \(y=x^2-5x+6\) es una parábola, para determinar los elementos distinguidos completemos cuadrado y obtenemos
\begin{equation*}
(x-\frac{5}{2})^2= 4\frac{1}{4}(y+\frac{1}{4}),
\end{equation*}
cuyo vértice es \(\left( \frac{5}{4},-\frac{1}{4} \right)\text{,}\) para tener una mejor gráfica, construyamos una tabla con algunos valores, para ello
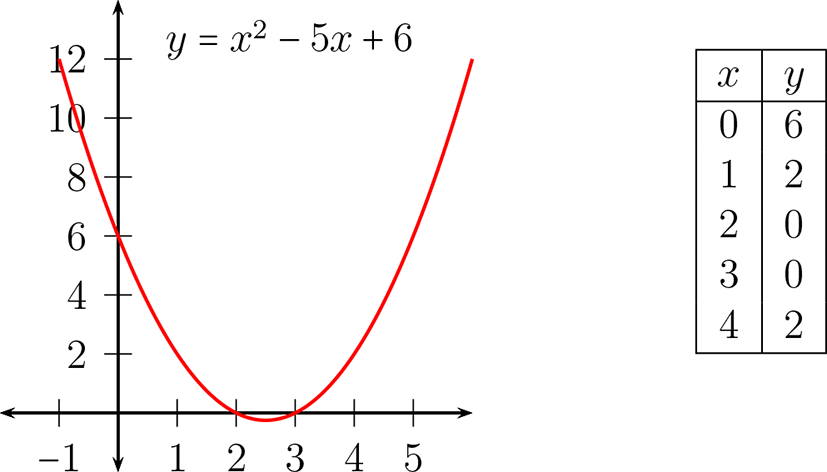
Usando la gráfica podemos constatar que el dominio es \(\mathbb{R} \) y el recorrido es \([-\frac{1}{4},\infty[\text{.}\)
Revisemos el recorrido para ello consideremos la ecuación de segundo grado
\begin{equation*}
\begin{array}{rll}
x^2-5x+6-y = \amp 0 \amp \\
x = \amp \frac{5\pm \sqrt{25-4(6-y)}}{2} \amp \\
x = \amp \frac{5\pm \sqrt{1+4y}}{2} \amp
\end{array}
\end{equation*}
Luego la única restricción es que el discriminante debe ser no negativo, es decir
\begin{equation*}
1+4y \geq 0 \Leftrightarrow y \geq -\frac{1}{4}
\end{equation*}
Por lo tanto el recorrido de \(f\) es \([-\frac{1}{4},\infty[\) .