[skip-to-content]

Sección 2.6 Elipse

Definición 2.6.1

Una elipse es el conjunto de todos los puntos tales que la suma de las distancias a dos puntos fijos es constante, los dos puntos fijos son llamados focos.

Sean \(F_{1} , F_{2} \in \mathbb{R}^{2}\) donde \(F_{1}\) y \(F_{2}\) representan los focos de la elipse y \(P\) un punto de la elipse, luego

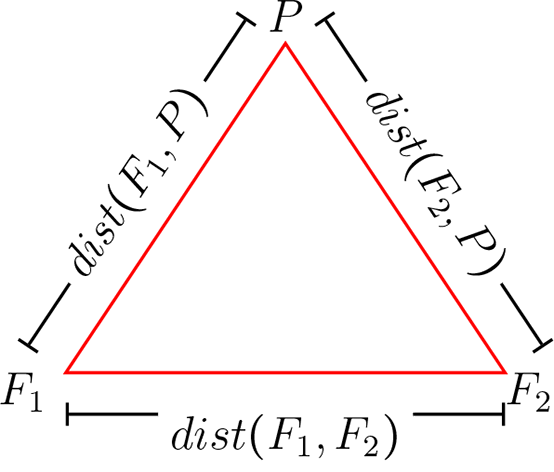
\begin{equation*} dist(P,F_{1}) + dist(P,F_{2}) = r \end{equation*}

Repitiendo el proceso para todos los puntos del plano que satisfacen la definición de la elipse tenemos el conjunto

\begin{equation*} \mathcal{E}_{F_{1}, F_{2}} = \{ P \in \mathbb{R}^{2} \mid dist(P,F_{1}) + dist(P,F_{2}) =r \} \end{equation*}

Si graficamos todos los puntos que pertenecen a \(\mathcal{E}_{F_{1}, F_{2}}\) tenemos lo siguiente:

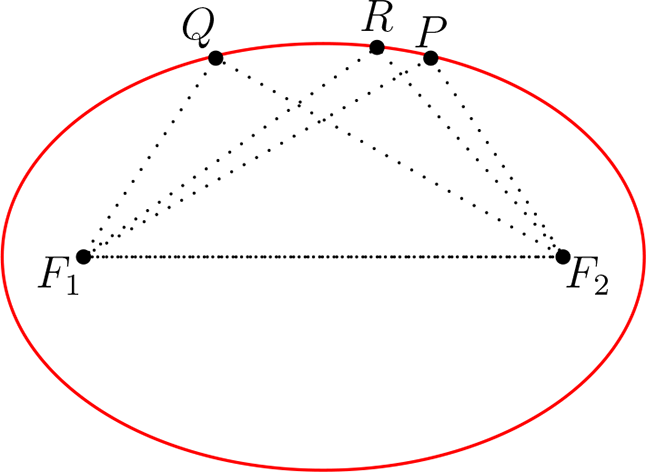
Consideremos la distancia entre los focos \(dist(F_{1},F_{2})\) y el punto medio que hay entre ellos que llamaremos centro de la elipse que denotaremos con la letra \(C\) y \(l \in \mathbb{R}^{2}\) la recta que pasa por ambos focos llamada el eje focal de la elipse. Por último, la longitud de la sumas de las distancias se llama longitud del eje mayor

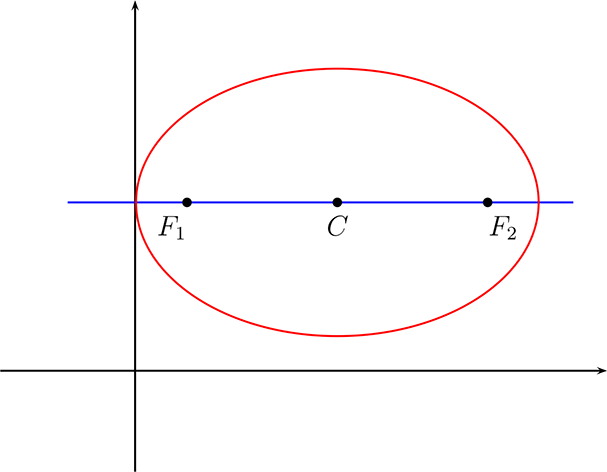
Subsección 2.6.1 Ecuación de la elipse con eje focal paralelo al eje \(X\)

Sea \(C,F_{1},F_{2} \in \mathbb{R}^{2}\text{,}\) con \(C = (h,k)\) el centro de la elipse, \(F_{1}\) y \(F_{2}\) los focos y \(P = (x,y) \in \mathcal{E}_{F_{1}, F_{2}}\) un punto cualquiera que pertenece a la elipse.

Como \(C = (h,k)\) y el eje focal paralelo al eje \(X\) luego \(F_{1}=(h+c,k)\text{,}\) \(F_{2}=(h-c,k)\text{,}\) de este modo tenemos la gráfica de la elipse para este caso.

A continuación, describiremos la ecuación de la elipses, para ellos consideremos los siguiente

\begin{equation*} \begin{array}{rcl} dist(F_{1},P) + dist(F_{2},P) \amp =\amp 2a \\ \sqrt{(x-h-c)^{2}+(y-k)^{2}} + \sqrt{(x-h+c)^{2}+(y-k)^{2}} \amp =\amp 2a \end{array} \end{equation*}

Realizando el cambio de variable \(u=x-h\) y \(v= y-k\text{,}\) para simplificar el calculo obtenemos

\begin{equation*} \begin{array}{rcl} 2a \amp =\amp dist(P,F_{1}) + dist(P,F_{2}) \\ 2a \amp =\amp \sqrt{(u-c)^{2} + v^{2}} + \sqrt{(u+c)^{2} + v^{2}} \\ 2a - \sqrt{(u+c)^{2} + v^{2}} \amp =\amp \sqrt{(u-c)^{2} + v^{2}} \ \ \ /()^{2} \ \ (*)\\ (2a - \sqrt{(u+c)^{2} + v^{2}})^{2} \amp =\amp (\sqrt{(u-c)^{2} + v^{2}})^{2} \\ 4a^{2} - 4a \sqrt{(u+c)^{2} +v^{2}} + (u+c)^{2} + v^{2} \amp =\amp (u-c)^{2} +v^{2} \\ (u+c)^{2} -(u-c)^{2}+4a^2 \amp =\amp 4a \sqrt{(u+c)^{2} +v^{2}} \\ 4a^2+4uc \amp =\amp 4a \sqrt{(x+c)^{2}+v^{2}} \ \ \ / \frac{1}{4}\\ a^{2} + uc \amp =\amp a \sqrt{(u+c)^{2} +v^{2}} \ \ \ /()^{2} \ \ \ (\ast) \\ a^{4} + 2a^{2}uc + u^{2}c^{2} \amp =\amp a^{2}((u+c)^{2} + v^{2}) \\ a^{4} + 2a^{2}uc + u^{2}c^{2} \amp =\amp a^{2}(u^{2} + 2uc +c^{2} + v^{2}) \\ a^{4} + 2a^{2}uc + u^{2}c^{2} \amp =\amp a^{2}u^{2} + 2a^{2}uc +a^{2}c^{2} + a^{2}v^{2} \\ a^{2}u^{2} - u^{2}c^{2} + a^{2}c^{2} + a^{2}v^{2} - a^{4} \amp =\amp 0 \\ u^{2} (a^{2} - c^{2}) + a^{2}v^{2} \amp =\amp a^{4} - a^{2}c^{2} \\ u^{2} (a^{2} - c^{2}) + a^{2}v^{2} \amp =\amp a^{2}(a^{2} - c^{2}) \ \ / \frac{1}{a^{2}(a^2-c^{2})} \\ \frac{u^{2}}{a^{2}} + \frac{v^{2}}{a^{2} - c^{2}} \amp =\amp 1 \end{array} \end{equation*}

Como \(2a \gt 2c\) entonces \(a^{2} - c^{2} \gt 0\text{,}\) sea \(b^{2} = a^{2} - c^{2} \lt a^{2}\text{,}\) luego \(b \lt a\text{.}\)

Reemplazando tenemos

\begin{equation*} \begin{array}{rcl} \frac{u^{2}}{a^{2} } + \frac{ v^{2}}{b^{2}} \amp =\amp 1 \end{array} \end{equation*}

Observación: Para lograr este resultado debemos considerar las dos restricciones (*), la primera de ella es:

\begin{equation*} 2a -\sqrt{(u+c)^{2} + v^{2}} \geq 0 \Leftrightarrow (u+c)^{2} +v^{2}\leq (2a)^2 \end{equation*}

y corresponde a circunferencias con centro en \(F_2\) y de radio menor que \(2a\text{,}\) la segunda restricción es

\begin{equation*} 4a^2+4uc \geq 0 \Leftrightarrow -\frac{a^2}{c}\leq u, \end{equation*}

y son rectas paralelas al eje \(v\text{,}\) formando el semiplano derecho, además note que \(-\frac{a^2}{c}\lt -a \text{,}\) es decir, es el semiplano a la derecha de \(-a \) .

Encuentre la ecuación de la elipse de centro en el origen, el valor de \(a=4\text{,}\) eje focal paralelo al eje \(X\) y pasa por el punto \(P=(3,2)\text{.}\)

Solución 1

Como su centro esta en el origen y \(a=4\) tenemos que la ecuación de la elipse esta dada por:

\begin{equation*} \begin{array}{rcl} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}\amp =\amp 1\\ \frac{x^{2}}{4^{2}} + \frac{y^{2}}{b^{2}}\amp =\amp 1\\ \frac{x^{2}}{16} + \frac{y^{2}}{b^{2}}\amp =\amp 1 \end{array} \end{equation*}

Luego la elipse pasa por el punto \(P=(3,2)\) entonces satisface su ecuación

\begin{equation*} \begin{array}{rcl} \frac{x^{2}}{16} + \frac{y^{2}}{b^{2}}\amp =\amp 1 \\ \frac{3^{2}}{16} + \frac{2^{2}}{b^{2}}\amp =\amp 1 \\ \frac{9}{16} + \frac{4}{b^{2}}\amp =\amp 1 \ \ / \cdot 16b^{2}\\ 9b^{2} + 4 \cdot 16 \amp =\amp 16b^{2} \\ 64 \amp =\amp 16b^{2}-9b^{2} \\ 64 \amp =\amp 7b^{2} \end{array} \end{equation*}

Luego el valor de \(b^{2}\) es:

\begin{equation*} \begin{array}{rcl} b^{2} \amp =\amp \frac{64}{7} \lt a^2=16 \end{array} \end{equation*}

Por lo tanto, la ecuación de la elipse es

\begin{equation*} \frac{x^{2}}{16} + \frac{y^{2}}{\frac{64}{3}}=1 \end{equation*}

Encuentre la ecuación de la elipse de centro en el punto \((1,3)\text{,}\) el valor de \(a=4\text{,}\) eje focal paralelo al eje \(X\) y pasa por el punto \(P=(2,5)\text{.}\)

Solución 2

Como su centro esta en el origen y \(a=4\) tenemos que la ecuación de la elipse esta dada por:

\begin{equation*} \begin{array}{rcl} \frac{(x-1)^{2}}{a^{2}} + \frac{(y-3)^{2}}{b^{2}}\amp =\amp 1\\ \frac{(x-1)^{2}}{16} + \frac{(y-3)^{2}}{b^{2}}\amp =\amp 1 \end{array} \end{equation*}

Luego la elipse pasa por el punto \(P=(2,7)\) entonces satisface su ecuación

\begin{equation*} \begin{array}{rcl} \frac{(x-1)^{2}}{16} + \frac{(y-3)^{2}}{b^{2}}\amp =\amp 1 \\ \frac{1^{2}}{16} + \frac{2^{2}}{b^{2}}\amp =\amp 1 \ \ / \cdot 16b^{2}\\ b^{2} + 4 \cdot 16 \amp =\amp 16b^{2} \\ 64 \amp =\amp 15b^{2} \end{array} \end{equation*}

Luego el valor de \(b^{2}\) es:

\begin{equation*} \begin{array}{rcl} b^{2} \amp =\amp \frac{64}{15} \lt a^2 =16 \end{array} \end{equation*}

Por lo tanto, la ecuación de la elipse es

\begin{equation*} \frac{(x-1)^{2}}{16} + \frac{(y-3)^{2}}{\frac{64}{15}}=1 \end{equation*}

Subsección 2.6.2 Ecuación de la elipse con eje focal en el eje \(Y\)

Sea \(C,F_{1},F_{2} \in \mathbb{R}^{2}\) y \(P \in \mathcal{E}_{F_{1}, F_{2}} \text{,}\) donde \(C = (h,k)\) representa el centro de la elipse, \(F_{1}\) y \(F_{2}\) los focos y \(P = (x,y)\) un punto cualquiera que pertenece a la elipse.

Como el centro es \(C = (h,k)\) y el eje focal paralelo al eje \(Y\) luego \(F_{1}=(h,k+c)\) y \(F_{2}=(h,k-c)\text{,}\) por lo cual tenemos

\begin{equation*} \begin{array}{rcl} dist(F_{1},P) + dist(F_{2},P) \amp =\amp 2a \\ \sqrt{(x-h)^{2}+(y-k-c)^{2}} + \sqrt{(x-h)^{2}+(y-k+c)^{2}} \amp =\amp 2a \end{array} \end{equation*}

Observemos la gráfica de la elipse para este caso.

Realizando el cambio de variable \(v = x-h \ \ \ \text{y} \ \ \ u=y-k \)

\begin{equation*} \begin{array}{rcl} dist(F_{1},P) + dist(F_{2},P) \amp =\amp 2a \\ \sqrt{(x-h)^{2}+(y-k-c)^{2}} + \sqrt{(x-h)^{2}+(y-k+c)^{2}} \amp =\amp 2a \\ \sqrt{(v)^{2}+(u-c)^{2}} + \sqrt{(v)^{2}+(u+c)^{2}} \amp =\amp 2a \end{array} \end{equation*}

Y es un expresión igual a la obtenida en el caso anterior \((\ast)\) de la sección anterior, luego usando el mismo desarrollo tenemos

\begin{equation*} \begin{array}{rcl} u^{2} (a^{2} - c^{2}) + v^{2}x^{2} \amp =\amp a^{2}(a^{2} - c^{2}) \end{array} \end{equation*}

de manera similar definimos \(b^{2} = a^{2} - c^{2} \lt a^{2} \) con lo cual

\begin{equation*} \frac{u^{2}}{a^{2} } + \frac{ v^{2}}{b^{2}} = 1 \end{equation*}

volviendo a las variables originales obtenemos

\begin{equation*} \frac{(x-h)^{2}}{b^{2} } + \frac{ (y-k)^{2}}{a^{2}} = 1 \end{equation*}

Encuentre la ecuación de la elipse de centro en el origen, el valor de \(a=6\text{,}\) eje focal paralelo al eje \(Y\) y pasa por el punto \(P=(2,5)\text{.}\)

Solución 1

Como su centro esta en el origen y \(a=6\) tenemos que la ecuación de la elipse esta dada por:

\begin{equation*} \begin{array}{rcl} \frac{x^{2}}{b^{2}} + \frac{y^{2}}{a^{2}}\amp =\amp 1\\ \frac{x^{2}}{b^{2}} + \frac{y^{2}}{36}\amp =\amp 1 \end{array} \end{equation*}

Luego la elipse pasa por el punto \(P=(2,5)\) entonces satisface su ecuación

\begin{equation*} \begin{array}{rcl} \frac{x^{2}}{b^{2}} + \frac{y^{2}}{36}\amp =\amp 1 \\ \frac{4}{b^{2}} + \frac{25}{36}\amp =\amp 1 \ \ / \cdot 36b^{2}\\ 4 \cdot 36 + 25b^{2} \amp =\amp 36b^{2} \\ 144 \amp =\amp 36b^{2}-25b^{2} \\ 144 \amp =\amp 11b^{2} \\ b^{2} \amp =\amp \frac{144}{11} \end{array} \end{equation*}

Por lo tanto la ecuación de la elipse es

\begin{equation*} \frac{x^{2}}{\frac{144}{11}} + \frac{y^{2}}{36}=1 \end{equation*}

Encuentre la ecuación de la elipse de centro \((4,3)\text{,}\) el valor de \(a=6\text{,}\) eje focal paralelo al eje \(Y\) y pasa por el punto \(P=(2,5)\text{.}\)

Solución 2

Como su centro esta en \((h,k)=(4,3)\) y \(a=6\) tenemos que la ecuación de la elipse esta dada por:

\begin{equation*} \begin{array}{rcl} \frac{(x-h)^{2}}{b^{2}} + \frac{(y-k)^{2}}{a^{2}}\amp =\amp 1\\ \frac{(x-h)^{2}}{b^{2}} + \frac{(y-k)^{2}}{6^{2}}\amp =\amp 1\\ \frac{(x-4)^{2}}{b^{2}} + \frac{(y-3)^{2}}{36}\amp =\amp 1 \end{array} \end{equation*}

Luego la elipse pasa por el punto \(P=(2,5)\) entonces satisface su ecuación

\begin{equation*} \begin{array}{rcl} \frac{(x-4)^{2}}{b^{2}} + \frac{(y-3)^{2}}{36}\amp =\amp 1 \\ \frac{(4-2)^{2}}{b^{2}} + \frac{(3-5)^{2}}{36}\amp =\amp 1 \\ \frac{4}{b^{2}} + \frac{4}{36}\amp =\amp 1 \ \ / \cdot 36b^{2}\\ 4 \cdot 36 + 4b^{2} \amp =\amp 36b^{2} \\ 144 \amp =\amp 36b^{2}-4b^{2} \\ 144 \amp =\amp 32b^{2} \end{array} \end{equation*}

Luego el valor de \(b^{2}\) es:

\begin{equation*} \begin{array}{rcl} b^{2} \amp =\amp \frac{144}{32}=\frac{9}{2} \end{array} \end{equation*}

Por lo tanto la ecuación de la elipse es

\begin{equation*} \frac{(x-4)^{2}}{\frac{9}{2}} + \frac{(y-3)^{2}}{36}=1 \end{equation*}

Observación: Consideremos la ecuación de la elipse donde el eje focal es paralelo al eje \(X\text{,}\) para ello sean \(C = (h,k)\) el centro de la elipse, \(F_{1}\) y \(F_{2}\) los focos y \(P = (x,y)\) un punto cualquiera que pertenece a la elipse.

\begin{equation*} \begin{array}{rcl} \frac{(x-h)^{2}}{a^{2} } + \frac{ (y-k)^{2}}{b^{2}} = 1 \end{array} \end{equation*}

Luego desarrollando la ecuación obtenemos

\begin{equation*} \begin{array}{rcl} \frac{(x-h)^{2}}{a^{2} } + \frac{ (y-k)^{2}}{b^{2}} \amp =\amp 1 \ \ /(a^{2}b^{2}) \\ b^{2}[(x-h)^{2}] + a^{2} [(y-k)^{2}] \amp =\amp a^{2} b^{2} \\ b^{2}[x^{2} - 2xh + h^{2}] + a^{2}[y^{2} - 2yk + k^{2}] \amp =\amp a^{2}b^{2} \\ x^{2}b^{2} - 2xhb^{2} + h^{2}b^{2} + y^{2}a^{2} - 2yka^{2} + k^{2}a^{2} \amp =\amp a^{2}b^{2} \\ x^{2}b^{2} - 2xhb^{2} + y^{2}a^{2} - 2yka^{2} + k^{2}a^{2} + h^{2}b^{2} - a^{2}b^{2} \amp =\amp 0 \end{array} \end{equation*}

Definimos las siguientes constantes \(A_{1},B_{1},C_{1},D_{1},E_{1} \in \mathbb{R}\) dadas por

\begin{equation*} \begin{array}{rcl} A_{1} = b^{2}; \ \ B_{1} = -2hb^{2}; \ \ C_{1} = a^{2}; \ \ D_{1} = -2ka^{2}; \ \ E_{1} = k^{2}a^{2} + h^{2}b^{2} - a^{2}b^{2}. \end{array} \end{equation*}

Entonces tenemos que la ecuación general de la elipse para este caso está dada por:

\begin{equation*} \begin{array}{rcl} A_{1}x^{2} + B_{1}x + C_{1}y^{2} + D_{1} y + E_{1} = 0 \end{array} \end{equation*}

Ahora consideremos la ecuación de la elipse, con el eje focal es paralelo al eje \(Y\) dada por:

\begin{equation*} \begin{array}{rcl} \frac{(x-h)^{2}}{b^{2} } + \frac{ (y-k)^{2}}{a^{2}} = 1 \end{array} \end{equation*}

Haciendo un desarrollo similar al anterior, podemos definir \(A_{2},B_{2},C_{2},D_{2},E_{2} \in \mathbb{R}\) tales que

\begin{equation*} \begin{array}{rcl} A_{2} = a^{2}; \ \ B_{2} = -2ha^{2}; \ \ C_{2} = b^{2}; \ \ D_{2} = -2kb^{2}; \ \ E_{2} = k^{2}b^{2} + h^{2}a^{2} - a^{2}b^{2}. \end{array} \end{equation*}

Entonces tenemos que la ecuación general de la elipse para este caso está dada por:

\begin{equation*} \begin{array}{rcl} A_{2}x^{2} + B_{2}x + C_{2}y^{2} + D_{2} y + E_{2} = 0 \end{array} \end{equation*}

Observación: En algunos textos considera la primer condiciones solamente, pero debe notar que la ecuación \(x^2+4y^2+1=0\text{,}\) en el plano real tiene conjunto solución vacío, por ello no es fácil aceptar que es una elipse, ya que las suma de positivos es positiva, nunca cero.

Hallar la ecuación de la elipse de centro \((1,2)\text{,}\) uno de los focos es \((6,2)\) y que pasa por el punto \((4,6)\)

Solución 3

Como su centro es \((1,2)\) y el eje focal es paralelo al eje \(X\text{.}\) Luego su ecuación esta dada por:

\begin{equation*} \begin{array}{rcl} \frac{(x-h)^{2}}{a^{2}} + \frac{(y-k)^{2}}{b^{2}} \amp =\amp 1 \\ \frac{(x-1)^{2}}{a^{2}} + \frac{(y-2)^{2}}{b^{2}} \amp =\amp 1 \end{array} \end{equation*}

Ya que pasa por el punto \((4,6)\)

\begin{equation*} \begin{array}{rcl}\label{ambar} \frac{(x-1)^{2}}{a^{2}} + \frac{(y-2)^{2}}{b^{2}} \amp =\amp 1 \\ \frac{(3)^{2}}{a^{2}} + \frac{(4)^{2}}{b^{2}} \amp =\amp 1 \\ \frac{9}{a^{2}} + \frac{16}{b^{2}} \amp =\amp 1 \end{array} \end{equation*}

Tenemos que la distancia del centro al foco es:

\begin{equation*} \begin{array}{rcl} c= dist(C,F) = \sqrt{(1-6)^{2}+(2-2)^{2}} = \sqrt{(-5)^{2}} = \sqrt{25} =5. \end{array} \end{equation*}

Entonces tenemos

\begin{equation*} \begin{array}{rcl} c^{2}\amp =\amp a^{2}-b^{2} \\ b^{2}\amp =\amp a^{2}-25 \end{array} \end{equation*}

reemplazando en la siguiente ecuación

\begin{equation*} \begin{array}{rcl} \frac{9}{a^{2}} + \frac{16}{b^{2}} \amp =\amp 1\\ \frac{9}{a^{2}} + \frac{16}{a^{2}-25} \amp =\amp 1 \ / \cdot (a^{2}-25)a^{2} \\ 9(a^{2}-25) + 16a^{2} \amp =\amp a^{2}(a^{2}-25) \\ a^{4}-25a^{2}-16a^{2}-9a^{2} + 225\amp =\amp 0 \\ a^{4}-50a^{2}+225\amp =\amp 0 \end{array} \end{equation*}

Sea \(u=a^{2}\) entonces

\begin{equation*} u^{2}-50u+225 =0 \end{equation*}

Luego

\begin{equation*} \begin{array}{rcl} u \amp =\amp \frac{50 \pm \sqrt{2500 - 900}}{2}= \frac{50 \pm \sqrt{1600}}{2}= \frac{50 \pm 40}{2} \end{array} \end{equation*}

Entonces

\begin{equation*} \begin{array}{rcl} u_{1} = \frac{50+40}{2} \amp \text{y} \amp u_{2}= \frac{50-40}{2} \\ u_{1} = \frac{90}{2} \amp \text{y} \amp u_{2}= \frac{10}{2} \\ u_{1} = 45 \amp \text{y} \amp u_{2}= 5 \end{array} \end{equation*}

Por lo tanto

\begin{equation*} \begin{array}{rcl} a^{2}=45 \amp \text{o} \amp a^{2}=5 \end{array} \end{equation*}

Si \(a^{2}=5\) tenemos

\begin{equation*} \begin{array}{rcl} b^{2}\amp =\amp a^{2}-25 = 5-25 = -20 \ (\Rightarrow \Leftarrow) \end{array} \end{equation*}

Entonces \(a^{2}=45\text{,}\) luego

\begin{equation*} b^{2}=a^{2}-25= 45-25=20 \end{equation*}

Por lo tanto, al reemplazar los valores obtenido \(a^{2}\) y \(b^{2}\text{,}\) se tiene la ecuación de la elipse solicitada

\begin{equation*} \frac{(x-1)^{2}}{45}+\frac{(y-2)^{2}}{20}=1 \end{equation*}

Subsección 2.6.3 Ejercicios Propuestos

  1. Grafique y encuentre todos los elementos de la elipse de la ecuación.

    1. \(9x^{2}+2y^{2}+36x+4y+20=0\)
    2. \(16x^{2}+9y^{2}-64x+54y+1=0\)
    3. \(25x^{2}+16y^{2}+150x-64y=102\)
    4. \(4x^{2}+6y^{2}=12\)
    5. \(x^{2}+4y^{2}-6x+16y+21=0\)
    6. \(4x^{2}+9y^{2}+32x-18y+37=0\)
    7. \(x^{2}+4y^{2}-10x-40y+109=0\)

  2. Obtener la ecuación de la elipse cuyos focos son \((-1,0)\) y \((1,0)\) y su diámetro mayor es \(6\text{.}\)

    [Resp. \(\frac{x^{2}}{9} + \frac{y^{2}}{8}=1\)]

  3. Hallar la ecuación de la elipse de centro \((1,2)\text{,}\) uno de los focos es \((6,2)\) y que pasa por el punto \((4,6)\text{.}\)

    [Resp. \(\frac{(x-1)^{2}}{45} + \frac{(y-2)^{2}}{20}=1\) ]

  4. Determinar las coordenadas de los focos de la elipse \(2x^{2}+7y^{2}=3\)

    [Resp.\ \(F_{1}= (\sqrt{\frac{15}{14}},0) \ , \ F_{2} = (-\sqrt{\frac{15}{14}},0)\) ]

  5. Hallar los vértices y el área de un cuadrado con lados paralelos a los ejes de coordenados inscrito en la elipse de ecuación \(9x^{2}+16y^{2}=100\text{.}\)

    [Resp. \(A= 16\) , \(V_{1}=(0,-0_\cdot4) \ , \ V_{2}=(0,0_\cdot4) \ , \ V_{3}=(-0_\cdot3,0) \ , \ V_{4}=(0_\cdot 3,0)\)]

  6. El centro de una elipse esta en el punto \((2,-4)\) el vértice y foco de un mismo lado del centro están en los puntos \((-2,-4)\) y \((-1,-4)\) respectivamente. Hallar la ecuación de la elipse.

    [Resp. \(\frac{(x-2)^{2}}{16} + \frac{(y+4)^{2}}{7}=1\) ]

  7. Una elipse tiene su centro en el origen y su eje mayor coincide con el eje \(X\) . Hallar su ecuación sabiendo que pasa por los puntos \((\sqrt{6} , -1)\) y \((2 , \sqrt{2})\text{.}\)

    [Resp. \(\frac{x^{2}}{8} + \frac{y^{2}}{4}=1\) ]

  8. Hallar la ecuación de la elipse que pasa por el punto \((\frac{\sqrt{7}}{2},3)\text{,}\) tiene su centro en el origen, su eje menor coincide con el eje \(X\) y la longitud de su eje mayor es el doble de la de su eje menor.

    [Resp. \(\frac{x^{2}}{4} + \frac{y^{2}}{16}=1\) ]

  9. Hallar la ecuación de la elipse que contiene a los siguientes puntos \((1,3)\text{,}\) \((-1,4)\text{,}\) \((0, 3-\frac{\sqrt{3}}{2})\) y \((-3,3)\) y tiene sus ejes paralelos a los coordenados.

    [Resp. \(x^{2}+4y^{2}+2x-24y+33=0\) ]

  10. Hallar e identificar la ecuación del lugar geométrico de un punto que se mueve de tal manera que su distancia del eje \(Y\) es siempre igual al doble de su distancia del punto \((3,2)\text{.}\)

    [Resp. \(3x^{2}+4y^{2}-24x-16y+52=0\) ]

  11. Desde cada punto de la circunferencia \(x^{2}+y^{2}+4x+4y-8=0\text{,}\) se traza una perpendicular al diámetro paralelo al eje \(X\text{.}\) Hallar e identificar la ecuación del lugar geométrico de los puntos medios de estas perpendiculares.

    [Resp. \(x^{2}+4y^{2}+4x+16y+4=0\) ]