Proposición 4.1.1
Sean \(\alpha,\beta \in \mathbb{R}\text{,}\) donde \(\beta\) es el ángulo medido en grados sexagesimales y \(\alpha\) el ángulo medido en radianes entonces
\begin{equation*}
\frac{\beta}{180} = \frac{\alpha}{\pi}
\end{equation*}
Sección 4.1 Introducción
¶Un concepto previo y muy importante para introducir las funciones trigonométricas es el de ángulo, que es una figura geométrica plana que consiste en un sector del plano limitado por dos semirrectas con el punto extremo en común. Para medir un ángulo, situamos el punto extremo en el centro de circunferencia y uno de los lados en el semi-eje positivo \(X\text{,}\) decimos que el ángulo es positivo si se mide en sentido del contrario al movimiento del manecillas del reloj en caso contrario es {ángulo es negativo.
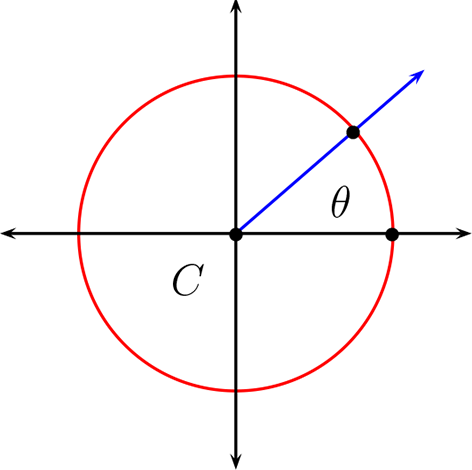
Existen varias formas de medir un ángulo, entre las más conocida están: Radianes, Sexagesimal y Centesimal, cada una de ella consiste en dividir, la circunferencia en \(2\pi\text{,}\) \(360\) o \(400\) partes iguales respectivamente.
Observación: Por medio de esta relación obtenemos
\begin{equation*}
\begin{array}{rcl}
\theta = \frac{180 \cdot \alpha}{\pi} \amp y \amp \alpha = \frac{\pi
\cdot \theta}{180}
\end{array}
\end{equation*}