[skip-to-content]

Sección 2.4 La Circunferencia

Definición 2.4.1

La circunferencia es el conjunto de todos los puntos que se encuentran a una misma distancia (radio) de otro punto fijo (centro) en el plano.

Denotaremos el centro de la circunferencia por \(Q=(h,k) \in \mathbb{R}^{2}\) y al radio por \(r \in \mathbb{R}^{+}\) que representa una longitud entre los puntos.

Sea \(P = (x_{1} , y_{1}) \in \mathbb{R}^{2}\text{.}\) Luego la distancia entre \(P\) y \(Q\) esta dada por

\begin{equation*} dist(Q,P) = \sqrt{(x_{1} - h)^{2} +(y_{1} - k)^{2}}. \end{equation*}

simplificando la expresión

\begin{equation*} \begin{array}{rcl} dist(Q,P) \amp =\amp r \\ \sqrt{(x_{1} - h)^{2} + (y_{1} - k)^{2}} \amp =\amp r \hspace{0.5cm} /()^{2} \\ (x_{1} - h)^{2} + (y_{1} - k)^{2} \amp =\amp r^{2} \end{array} \end{equation*}

lo cual debe cumplir cualquier punto que pertenece a la circunferencia. Así obtenemos

\begin{equation*} \begin{array}{rcl} \mathcal{C}_r(Q) \amp =\amp \{ P \in \mathbb{R}^{2}\;\;\; \mid \; dist(Q,P)=r \} \\ \mathcal{C}_r(Q) \amp =\amp \{ (x,y) \in \mathbb{R}^{2}\;\;\; \mid \; (x - h)^{2} + (y - k)^{2} = r^{2}\} \end{array} \end{equation*}

Observación: Al igual que el ejemplo Ejemplo 2.2.5 la ecuación de la circunferencia que tiene su centro en el origen, \((h,k) = (0,0)\text{,}\) y radio \(r\) esta dada por:

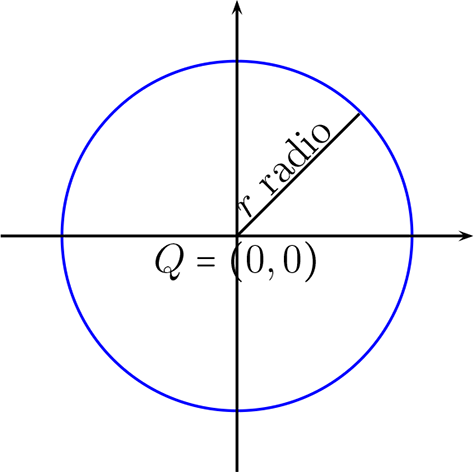
\begin{equation*} x^{2}+y^{2}= r^{2} \end{equation*}

Observación: Sean \(T \in \mathcal{C}_r(Q) , Q \in \mathbb{R}^{2} \) y \(r \in \mathbb{R}\) donde \(T = (x,y)\) , \(Q = (h,k)\) es el centro y \(r\) que es el radio entonces la ecuación de la circunferencia, la ecuación de la circunferencia la obtenemos de la propiedad Proposición 2.4.2 y es:

\begin{equation*} \begin{array}{rcl} (x - h)^{2} + (y - k)^{2} \amp =\amp r^{2} \end{array} \end{equation*}

Entonces

\begin{equation*} \begin{array}{rcl} (x - h)^{2} + (y - k)^{2} \amp =\amp r^{2} \\ x^{2} - 2xh + h^{2} + y^{2} - 2yk + k^{2} \amp =\amp r^{2} \\ x^{2} + y^{2} - 2xh - 2yk + k^{2}+ h^{2} - r^{2} \amp =\amp 0 \end{array} \end{equation*}

Definamos las siguientes variables

\begin{equation*} A = -2h, \quad B = -2k, \quad C= k^{2} + h^{2} - r^{2}. \end{equation*}

luego reemplazando obtenemos

\begin{equation*} x^{2} + y^{2} +Ax + By + C = 0 \end{equation*}

llama ecuación general de la circunferencia.

Subsección 2.4.1 Tangencia de una recta a la circunferencia

Una recta \(l\) es tangente a una circunferencia \(\mathcal{C}_r\) en el punto \(P \in l \cap \mathcal{C}_r \text{,}\) si la recta es perpendicular al radio de la circunferencia en el punto \(P\text{.}\)

Sean \(Q=(h,k)\) el centro de la circunferencia, \(P\in \mathbb{R}^{2}\) el punto de tangencia entre la recta \(l\) y la circunferencia. Por lo tanto \(l_{PQ}\) es perpendicular a \(l\text{,}\) lo que gráficamente tenemos dado por:

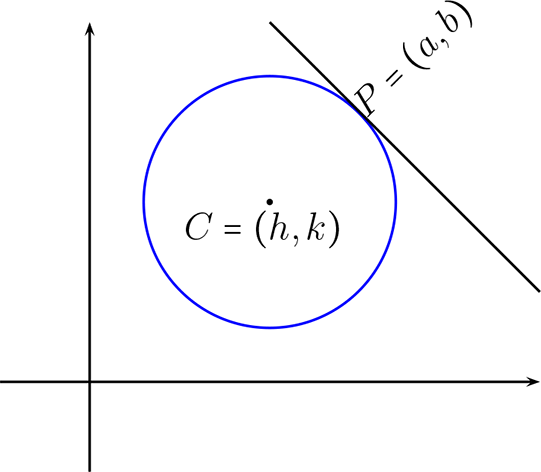
Encuentre la recta tangencia a la circunferencia \((x-1)^2+(y+3)^2=25\) en el punto \((4,1)\text{.}\)

Solución 1

Sea \(C:(x-1)^2+(y+3)^2=25\) y \(P=(4,1)\text{.}\)

Primero notemos que el punto \(P\) pertenece a la circunferencia, ya que \(3^2+4^2=25\text{,}\) además el centro de la circunferencia es \(Q=(1,-3)\text{.}\)

La recta que une el centro \(Q(1,-3)\) y el punto \(P\) tiene pendiente

\begin{equation*} m=\frac{-3-1}{1-4}=\frac{-4}{-3}=\frac{4}{3} \end{equation*}

Luego la recta perpendicular, tiene pendiente \(m'=-\frac{3}{4}\text{.}\)

Así tenemos que su ecuación es

\begin{equation*} y-1= -\frac{3}{4}(x-4) \end{equation*}

Por lo tanto, la recta tangente a \(C\) en el punto \(P\) es

\begin{equation*} 3x+4y=16. \end{equation*}

Encuentre \(P\) el punto de tangencia entre la circunferencia de radio \(\sqrt{17}\) y centro \((3,6)\text{,}\) con la recta \(l\) de pendiente \(m=\frac{1}{4}\) y que pasa por el punto \((12,4)\text{.}\)

Solución 2

Como el centro de la circunferencia es \((3,6)\) y su radio es \(\sqrt{17}\) tenemos que la ecuación de la circunferencia es:

\begin{equation*} \begin{array}{rcl} (x - 3)^{2} + (y - 6)^{2} \amp =\amp 17 \end{array} \end{equation*}

Ya que la recta tiene pendiente \(m=\frac{1}{4}\) y el punto \((12,4)\) pertenece a esta, entonces su ecuación es:

\begin{equation*} \begin{array}{rcl} y - b \amp =\amp m (x - a) \\ y - 4 \amp =\amp \frac{1}{4} (x - 12) \\ 4y-x \amp =\amp 4 \end{array} \end{equation*}

Luego, el punto \(P\) pertenece a la recta y a la circunferencia y de este modo tenemos el sistema

\begin{equation*} \begin{array}{rcc|} (x - 3)^{2} + (y - 6)^{2} \amp =\amp 17 \\ 4y-x\amp =\amp 4\\ \hline \end{array} \end{equation*}

Despejando tenemos que \(x=4y-4\text{,}\) reemplazando obtenemos

\begin{equation*} (4y-4 - 3)^{2} + (y - 6)^{2} = 17 \end{equation*}

Simplificando se obtiene que

\begin{equation*} y^2-4y+4=0 \end{equation*}

Que tiene las dos soluciones iguales, de este modo obtenemos que \(y=2\text{,}\) de ello se obtiene que \(x= 8-4=4\text{.}\)

Por lo tanto el punto de intersección es \((4,2)\text{,}\) el cual es fácil verificar que pertenece a la circunferencia \((4-3)^2+(2-6)^2=17\) y a la recta. Luego el punto pedido es \(P=(4,2)\text{.}\)

Subsección 2.4.2 Intersección entre una recta y una circunferencia

La intersección de una recta con una circunferencia da como resultado un conjunto que a lo más tiene dos puntos que se encuentran en el plano cartesiano, los cuales se pueden obtener a través de un sistema ecuaciones, es decir, un punto que pertenece a la recta y a la circunferencia satisfacen ambas ecuaciones.

Sean \((x - h)^{2} + (y - k)^{2} = r^{2}\) una circunferencia de radio \(r\) y centro \(Q=(h,k)\) y la recta de ecuación \(l: Ax+By+C=0\text{.}\)

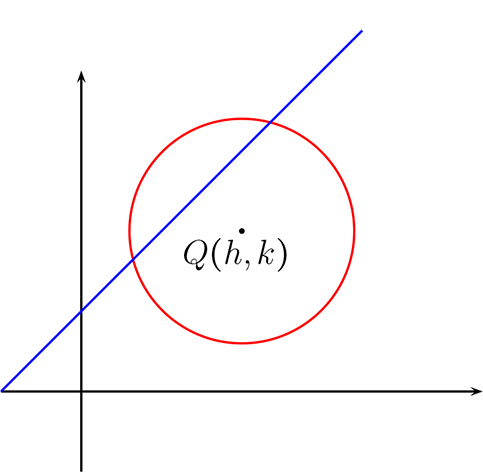
Sea \(P=(x,y) \in \mathbb{R}^{2}\) un punto de la intersección de la recta con la circunferencia:

\begin{equation*} \begin{array}{rcl|} (x - h)^{2} + (y - k)^{2} \amp = \amp r^{2} \\ Ax+By+C\amp =\amp 0\\ \hline \end{array} \end{equation*}

Veremos sólo el caso \(B \neq 0\text{,}\) despejando \(y\) en la ecuación segunda ecuación tenemos

\begin{equation*} y = m_1x + b_{1} \end{equation*}

Luego reemplazando en la ecuación en la segunda, obtenemos

\begin{equation*} (x - h)^{2} + ([m_1x + b_{1}] - k)^{2} = r^{2} \end{equation*}
\begin{equation*} x^{2} -2xh + h^{2} + [m_1x + b_{1}]^{2}- 2k [m_1 x + b_{1}] + k^{2} = r^{2} \end{equation*}
\begin{equation*} x^{2} -2xh + h^{2} + m_1^{2}x^{2} +2m_1b_{1}x + b^{2}_{1} -2km_1x - 2km_1b_{1} + k^{2} = r^{2} \end{equation*}
\begin{equation*} x^{2}(1 + m_1^{2}) + x(-2h + 2m_1 b_{1} -2km_1) + (h^{2} + b^{2}_{1} -2km_1b_{1} + k^{2} - r^{2}) =0 \end{equation*}

Sean

\begin{equation*} \begin{array}{ccl} a \amp =\amp 1 + m_1^{2} \\ b \amp =\amp -2h - 2 m_1^{2} x_{1} +2m_1 y_{1} -2km_1 \\ c \amp =\amp h^{2} + m_1^{2}x^{2}_{1}- 2m_1y_{1}x_{1} + y^{2}_{1} +2km_1x_{1} -2m_1y_{1} +k^{2} - r^{2} \end{array} \end{equation*}

reemplazando obtenemos

\begin{equation*} a x^{2} + bx + c = 0 \end{equation*}

Luego consideremos el discriminante de la ecuación que denotaremos por \(\Delta\text{.}\)

  1. Si \(\Delta \lt 0\text{,}\) se tiene que la ecuación tiene solución vacía en los reales, es decir, no hay puntos comunes a la recta y la circunferencia.

  2. Si \(\Delta = 0\text{,}\) se tiene que la ecuación tiene una única solución real, es decir, la intersección de la recta con la circunferencia es único el punto, lo cual indica que la recta \(l\) es tangente a la circunferencia.

  3. Si \(\Delta \gt 0\text{,}\) se tiene que la ecuación tiene dos soluciones reales, es decir, la intersección de la recta con la circunferencia tiene dos puntos, es una recta secante.

Dada la circunferencia de ecuación \((x-2)^{2}+(y-3)^{2}=4\text{.}\)

Determine cuales puntos de la circunferencia pertenecen a la recta, en cada uno de los siguientes casos.

  1. \(l_{1}: 3 \sqrt{3}+6-x=\sqrt{3}y \)

  2. \(l_{2}: x=y\)

  3. \(l_{3}: x-y=-5\)

Solución

Consideremos la circunferencia \((x-2)^{2}+(y-3)^{2}=4\) e interceptemos con la recta, luego se obtiene un sistema de ecuaciones, que debemos resolver en cada una de las alternativas

  1. \begin{equation*} \begin{array}{rcl|} (x-2)^{2}+(y-3)^{2}\amp =\amp 4 \\ 3 \sqrt{3}+6-x\amp =\amp \sqrt{3}y \\ \hline \end{array} \end{equation*}

    Despejando

    \begin{equation*} \begin{array}{cccccc} \sqrt{3}y \amp =\amp 3 \sqrt{3}+6-x \\ y \amp =\amp \frac{3\sqrt{3}+6-x}{\sqrt{3}} \\ y \amp =\amp 3 + \frac{6-x}{\sqrt{3}} \\ \end{array} \end{equation*}

    Reemplazando la variable obtenida, en la ecuación de la circunferencia obtenemos

    \begin{equation*} \begin{array}{rcl} (x-2)^{2}+(y-3)^{2}\amp =\amp 4 \\ (x-2)^{2}+\left(3 + \frac{6-x}{\sqrt{3}}-3\right)^{2}\amp =\amp 4 \\ (x-2)^{2}+\left( \frac{6-x}{\sqrt{3}}\right)^{2}\amp =\amp 4 \\ x^{2}-4x+4+ \frac{x^{2}-12x+36}{3}\amp =\amp 4 \ \ /\cdot 3 \\ 3x^{2}-12x + x^{2}-12x+36\amp =\amp 0 \\ 4x^{2} -24x+36\amp =\amp 0 \ \ / \cdot \frac{1}{4} \\ x^{2}-6x+9 \amp =\amp 0 \end{array} \end{equation*}

    Luego el discriminante \(\Delta= (6)^{2}-4 \cdot 1 \cdot 9=0\text{,}\) despejando \(x\) tenemos

    \begin{equation*} \begin{array}{rcl} x \amp =\amp \frac{6 \pm \sqrt{0}}{2} = \frac{6}{2} =3 \end{array} \end{equation*}

    Reemplazando en la recta, encontremos el valor de \(y\)

    \begin{equation*} y = 3+ \frac{6-x}{\sqrt{3}} = 3+ \frac{6-3}{\sqrt{3}} = 3 + \frac{3}{\sqrt{3}}= 3 + \frac{3 \sqrt{3}}{3} = 3 + \sqrt{3} \end{equation*}

    Por lo tanto el punto de intersección, cuando \(\Delta=0\text{,}\) es

    \begin{equation*} P = (3,3+ \sqrt{3}) \end{equation*}

  2. Consideremos ahora el segundo sistema de ecuaciones

    \begin{equation*} \begin{array}{rcl|} (x-2)^{2}+(y-3)^{2}\amp =\amp 4 \\ x \amp =\amp y \\ \hline \end{array} \end{equation*}

    Reemplazando la variable \(y\) ecuación de la recta, en la ecuación de la circunferencia obtenemos

    \begin{equation*} \begin{array}{rcl} (x-2)^{2}+(y-3)^{2}\amp =\amp 4 \\ (x-2)^{2}+(x-3)^{2}\amp =\amp 4 \\ x^{2}-4x+4+x^{2} -6x+9-4\amp =\amp 0 \\ 2x^{2} -10x+9\amp =\amp 0 \end{array} \end{equation*}

    Luego el discriminante \(\Delta = (10)^{2}-4 \cdot 2 \cdot 9= 28\text{,}\) y determinado las soluciones de la ecuación de segundo grado obtenemos

    \begin{equation*} \begin{array}{rcl} x \amp =\amp \frac{10 \pm \sqrt{28}}{4} = \frac{5 \pm \sqrt{7}}{2} \end{array} \end{equation*}

    Por lo tanto

    \begin{equation*} \begin{array}{rcl} x_{1} = \frac{5 + \sqrt{7}}{2} \amp \ \text{y} \ \amp x_{2} = \frac{5 - \sqrt{7}}{2} \end{array} \end{equation*}

    Reemplazando en la ecuación de la recta, encontremos \(y\)

    1. Si \(x = \frac{5 + \sqrt{7}}{2}\) entonces \(y = \frac{5+\sqrt{7}}{2}\)

    2. Si \(x = \frac{5 - \sqrt{7}}{2}\) entonces \(y= \frac{5 - \sqrt{7}}{2}\)

    Por lo tanto los puntos de intersección, cuando \(\Delta \lt 0\text{,}\) son

    \begin{equation*} \begin{array}{rcl} P_{1} = \Big( \frac{5 + \sqrt{7}}{2},\frac{5 + \sqrt{7}}{2} \Big) \amp \ y \ \amp P_{2}= \Big( \frac{5 - \sqrt{7}}{2},\frac{5 - \sqrt{7}}{2} \Big) \end{array} \end{equation*}

  3. Consideremos el sistema de ecuaciones

    \begin{equation*} \begin{array}{rcl|} (x-2)^{2}+(y-3)^{2}\amp =\amp 4 \\ x-y\amp =\amp -5 \\ \hline \end{array} \end{equation*}

    Despejando, obtenemos

    \begin{equation*} x = y-5 \end{equation*}

    Reemplazando ahora en la ecuación de la circunferencia obtenemos

    \begin{equation*} \begin{array}{rcl} (x-2)^{2}+(y-3)^{2}\amp =\amp 4 \\ (y-5-2)^{2}+(y-3)^{2}\amp =\amp 4 \\ (y-7)^{2}+(y-3)^{2}\amp =\amp 4 \\ y^{2}-14y+49+y^{2} -6y+9-4\amp =\amp 0 \\ 2y^{2} -20y+54\amp =\amp 0 \end{array} \end{equation*}

    Análogamente calculamos el discriminante y tenemos que \(\Delta = -2\text{,}\) luego la intersección de la circunferencia con la recta \(l_{3}\) es vacía, es decir no tiene puntos.

Gráficamente nos encontramos en la siguiente situación:

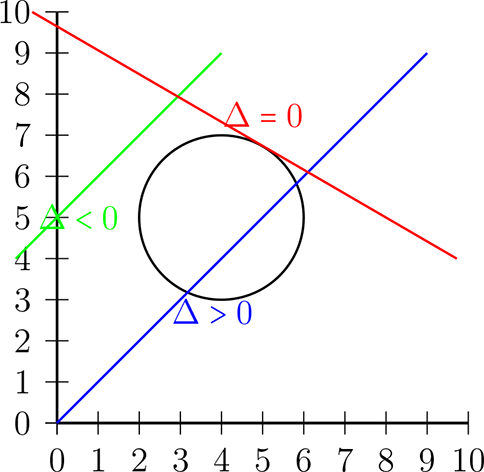
Subsección 2.4.3 Ejercicios Propuestos

  1. Considere la recta \(y-2x-c = 0\) y la circunferencia \(x^{2}+y^{2}= \frac{1}{4}\text{.}\) Determine el valor de \(c\) en cada caso

    1. La recta es tangente a la circunferencia. \([ Resp.\ \ c= \frac{-\sqrt{5}}{2} \ o \ c = \frac{\sqrt{5}}{2} ]\)

    2. La recta y circunferencia tienen intersección. \([ Resp.\ \ c \in \mathbb{R}- [\frac{-\sqrt{5}}{2}, \frac{\sqrt{5}}{2}] ]\)

  2. Encuentre la ecuación de la circunferencia que contiene al punto \((-1,-8)\) y que es tangente a \(3x-4y-4=0\) en el punto \((0,-1)\text{.}\)

    \([ Resp.\ x^{2}+y^{2} -6x+10y=-9 ]\)

  3. Hallar la ecuación de la circunferencia de radio es \(9\) y cuyo centro esta en la intersección de las rectas \(x-4y=1\) y \(2x-y=2\text{.}\)

    \([ Resp.\ x^{2}+y^{2}-2x=82 ]\)

  4. Hallar la ecuación de la circunferencia cuyo centro es \((0,-2)\) y es tangente a la recta \(5x-12y+2=0\text{.}\)

    \([ Resp.\ \ x^{2}+y^{2}+4y=0 ]\)

  5. Hallar la ecuación de la circunferencia cuyo centro es el vértice \(A=(-1,0)\) del triángulo \(ABC\) y es tangente a \(l_{BC}\) con \(B=(2, \frac{9}{4})\) y \(C=(5,0)\text{.}\)

    \([ Resp. \ x^{2}+y^{2}+2x = 323 ]\)

  6. Hallar la ecuación de la circunferencia que es tangente a las rectas \(l_{1}: x+y+4=0\) y \(l_{2}: 7x-y+4=0\text{,}\) y su centro se encuentra en la recta \(l_{3}: 4x+3y-2=0\text{.}\)

    \([ Resp.\ \ (x- \frac{11}{4})^{2} + (y+3)^{2}= \frac{225}{32} \ o \ (x+1)^{2} + (y-2)^{2}= \frac{1}{2} ]\)

  7. Considere la circunferencia de ecuación \(x^{2}+y^{2}+2ky=0\text{,}\) desde el punto \(A=(5,4)\) se traza la tangente a la circunferencia siendo \(Q\) el punto de tangencia. Determine el valor de \(k\) para que la longitud del segmento \(\overline{AQ}\) sea \(1\text{.}\)

    \([ Resp.\ \ k=-5 ]\)

  8. Considere la ecuación de la circunferencia \(x^{2}+y^{2}=8x+6y\text{.}\) Determine en cada caso la ecuación de la recta \(l\) que es tangente a la circunferencia y que pasa por:

    1. \(P=(8,6)\) . \([ Resp.\ \ l: 3y=-4x+50 ]\)

    2. \(Q=(11,4)\text{.}\) \([ Resp.\ \ l: 3y-4x+32=0 \ o \ l: 4y+3x-49 =0]\)

  9. Encuentre la ecuación de la recta que es tangente a la circunferencia de ecuación \(x^{2}-2x=2y-y^{2}\) en el punto \((2,2)\text{.}\)

    \([ Resp.\ \ x+y-4=0 ]\)

  10. Determine la ecuación de la circunferencia que pasa por los puntos \((2,-2),(-1,4)\) y \((4,6)\text{.}\)

    \([ Resp.\ \ (x- \frac{8}{3})^{2} + (y- \frac{25}{12})^{2} = \frac{2465}{144} ]\)

  11. Hallar la ecuación de la circunferencia cuyo centro esta sobre la recta \(x-2y-2=0\) y es tangente a cada una de las rectas \(x-y+2=0\) y \(x+y-1=0\text{.}\)

    \([ Resp.\ \ (x-5)^{2} + (y- \frac{3}{2})^{2} = \big( \frac{11}{2 \sqrt{2}} \big)^{2} \ o \ (x+ \frac{1}{2})^{2} + (y + \frac{5}{4})^{2} = \big( \frac{4}{\sqrt{2}} \big)^{2} ]\)

  12. Encuentre la ecuación de la circunferencia de radio \(\sqrt{13}\) que es tangente a la circunferencia \(x^{2}+y^{2}-4x+2y-47=0\) en el punto \((6,5)\text{.}\)

    \([ Resp.\ \ (x-8)^{2}+(y-8)^{2}=13 \ o \ (x-4)^{2}+(y-2)^{2} = 13 ]\)

  13. Hallar la ecuación de la circunferencia de radio \(\frac{5 \sqrt{2}}{2}\) y que pasa por la intersección de las circunferencias \(x^{2}+y^{2}+2x-6y-16=0\) y \(x^{2}+y^{2}-6x+2y=0\text{.}\)

    \([ Resp.\ \ x^{2}+y^{2}-x-3y-10=0 \ o \ x^{2}+y^{2}-7x+3y+2=0 ]\)