[skip-to-content]

Sección 3.3 Modelación

Modelar matemáticamente una situación de la vida cotidiana se refiere a identificar en un problema una expresión matemática concreta que represente algunos aspecto del problema, de modo que esta expresión nos permita obtener información actual o futura.

Esta expresión matemática puede expresarse mediante un enunciado o mediante una ecuación. En el siguiente ejemplo encontramos una situación la cual se puede modelar mediante una función.

Cuando hablamos del impuesto a la venta de ciertos artículos, nos referimos a una situación de la vida diaria, la cual podemos modelar de la siguiente forma; si \(x\) representa el valor del artículo en pesos sin impuesto y \(T\) es el impuesto a la venta del articulo, el cual es de un 19% sobre el valor de \(x\text{,}\) entonces podemos expresar \(T\) en función de \(x\) de la siguiente modo:

\begin{equation*} T(x)=\frac{19}{100}\cdot x \end{equation*}

con \(x \gt 0\)

Es decir, si tenemos un artículo cuyo valor es de 200 sin IVA, el impuesto a la venta se puede calcular usando la expresión matemática encontrada:

\begin{equation*} T(200)=\frac{19}{100}\cdot 200 =38 \end{equation*}

Observación: En el caso que el impuesto ya este incluido en el valor, tenemos que la función no es la misma, ya que

\begin{equation*} P= x+ 0,19x= 1,19x \end{equation*}

Luego si pagamos \($ 200\text{,}\) el costo del producto sin impuesto es \(1,19x=200\text{,}\) o bien \(x= \frac{200}{1.19}\approx 168.1 \) y el impuesto es

\begin{equation*} 0,19\frac{200}{1.19}\approx 31,9. \end{equation*}

Cuando las personas pagan y le extiende una factura tenemos el primer caso, y el segundo posibilidad es cuando se extiende una boleta, donde no figura los impuestos, sólo el valor final.

Considere un rectángulo ABCD con sus lados paralelos a los ejes, inscrito en la elipse \(9x^2+4y^2=36\text{.}\) Sea \(z\) la distancia entre un lado vertical del rectángulo y el eje \(y\text{.}\)

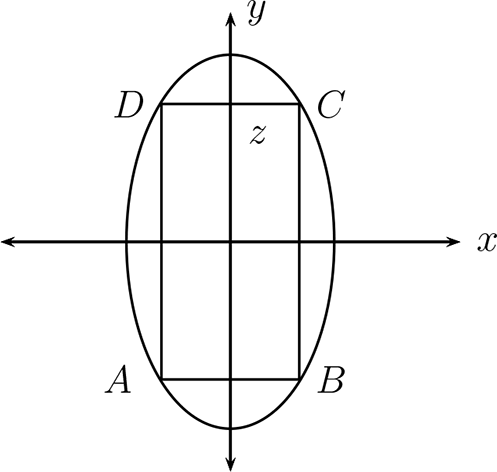
Determine el área del rectángulo en función de \(z\text{,}\) expresando claramente el dominio.

Solución 1

El área del rectángulo, es el producto de las longitudes de los lados, para ello sean

\begin{equation*} |\overline{AB}|=2z\wedge |\overline{BC}|=2y \end{equation*}

Luego el área del rectángulo en función de \(z\) y de \(y\) es la siguiente:

\begin{equation*} A=2z\cdot 2y=4zy \end{equation*}

Como el punto C pertenece a la elipse entonces satisface la ecuación \(9x^2+4y^2=36\text{,}\) despejamos \(y\)

\begin{equation*} \begin{array}{rll} 9z^2+4y^2 = \amp 36 \amp \\ 4y^2 =\amp 36-9z^2 \amp / (\frac{1}{4})\\ y^2 =\amp \frac{36}{4}-\frac{9}{4}z^2 /\sqrt{} \amp \frac{36}{4}-\frac{9}{4}z^2 \gt 0\\ |y|=\amp \sqrt{\frac{36}{4}-\frac{9}{4}z^2} \amp \\ |y|=\amp \frac{1}{2}\sqrt{36-9z^2} \amp \\ |y|=\amp \frac{1}{2}\sqrt{9(4-z^2)} \amp \\ \end{array} \end{equation*}

Como \(y\) representa una distancia, entonces el valor es positivo

\begin{equation*} y=\frac{3}{2}\sqrt{4-z^2} \end{equation*}

donde \({4-z^2} \gt 0.\)

Por lo tanto, el área en función de \(z\) queda determinada como sigue

\begin{equation*} A(z)=4z\cdot \frac{3}{2}\sqrt{4-z^2}=6z\sqrt{4-z^2} \end{equation*}

Ahora veremos cual es el dominio.

\begin{equation*} \begin{array}{rll} 4-z^2 \amp \geq 0 \amp \\ 4 \amp \geq z^2 \amp / \sqrt{}\\ 2 \amp \geq |z| \amp \\ \end{array} \end{equation*}
\begin{equation*} -2\leq z \leq 2 \end{equation*}

Como \(z\) es una distancia entonces

\begin{equation*} Dom (A)=]0,2[. \end{equation*}

Los extremos no se incluye, ya que las linea, no forma un rectángulo

Se desea construir una caja con tapa de base cuadrada con área no mayor de 100 \({cm}^2\) como en la figura, de volumen 252 \({cm}^3\text{.}\) Si el costo de la tapa es $2 por \({cm}^2\text{,}\) la base $5 por \({cm}^2\) y el costo de los lados es de $3 por \({cm}^2\text{,}\) exprese el costo \(C\) como función de \(x\) y el dominio de \(C\)

Solución 2

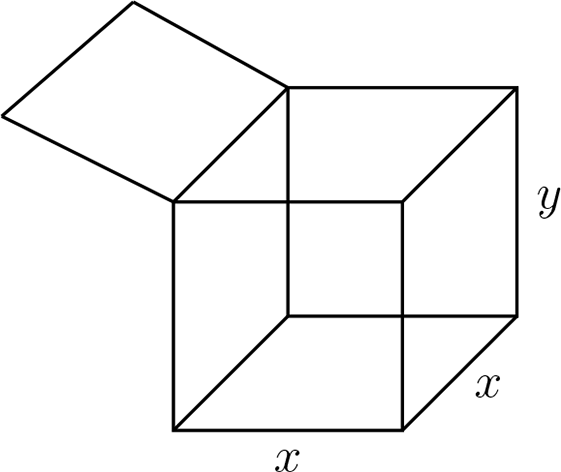
Dado que el volumen es \(V=252 cm^3\text{,}\) luego \(x^2y=252\text{,}\) ahora veremos el costo por lado

El costo de la tapa es de $2 por \(cm^2\text{.}\) La tapa tiene \(x^2cm^2\text{,}\) por lo tanto el costo de la tapa es $\(2x^2\text{.}\)

El costo de la base es de $5 por \(cm^2\text{.}\) La base tiene \(x^2cm^2\text{,}\) por lo tanto el costo de la base es \(5x^2\text{.}\)

El costo de los lados es de $3 por \(cm^2\text{.}\) Cada lado tiene \(xy cm^2\text{,}\) por lo tanto el costo de los lados es de $\(12xy\text{.}\)

El costo total de la caja es:

\begin{equation*} C=2x^2+5x^2+12xy \end{equation*}

pero \(y=\frac{252}{x^2}\)

Entonces la función queda determinada como

\begin{equation*} C(x)=7x^2+12x\cdot\frac{252}{x^2} \end{equation*}
\begin{equation*} C(x)=7x^2+\frac{3024}{x} \end{equation*}

donde el dominio de \(C\) es \(]0,10] \)

Subsección 3.3.1 Ejercicios Propuestos

  1. Si el radio basal \(r\) de un cono circular recto aumenta en un \(x\% \text{,}\) mientras que su altura \(h\) disminuye en un \(20\% \) formule una función en términos de \(x\) que permita obtener en qué porcentaje varían:

    1. El área basal del cono.

    2. Si el radio aumenta en \(15\% \) ¿en qué porcentaje varían el área basal y el volumen del cono?

  2. Una caja rectangular con la parte superior abierta tiene un volumen de \(10 m^3\text{.}\) La longitud de su base es el doble de su ancho. El material de la base tiene un costo de 10 dólares por \(m^2\text{,}\) el material de las caras laterales tiene un costo de 6 dólares por \(m^2\text{.}\)

    Expresar el costo de los materiales en función del ancho de la base.

  3. En una parcela, se desea encerrar dos porciones de terreno de igual área (como en la figura) con una malla de longitud \(L\text{.}\) Expresar el área de la parcela en función de \(x\text{.}\)

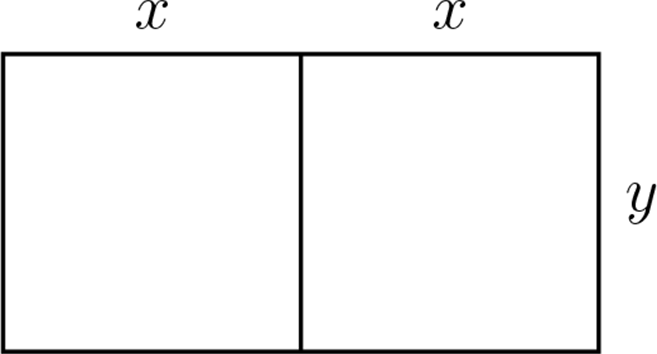
  4. El área de una piscina rectangular con bordes es de \(18 cm^2\text{.}\) Si el borde superior e inferior miden \(\frac{1}{3} m\) y los bordes laterales miden \(\frac{1}{4} m\text{.}\) Expresar el área comprendida entre los bordes en función de uno de los lados de la piscina.

  5. La asistencia media en un cine en el que la entrada vale $\(1200\) es de 100 personas. El empresario cree que cada vez que se reduce el precio en $\(80\text{,}\) el número de espectadores aumenta en 20.

    1. Determine la recaudación \(R\) en función del precio \(p\text{.}\)

    2. ¿Qué precio y número de espectadores producirán la mayor asistencia?

    3. ¿Cuál es la recaudación máxima por sesión?