Sección 3.7 Funciones Exponenciales
¶
Teorema 3.7.1
Sea \(a\in \mathbb{R}^+\text{,}\) \(x\in\mathbb{R} \text{,}\) entonces para cada \(a\) existe una función \(f:\mathbb{R}\longrightarrow \mathbb{R} \) tal que
\begin{equation*}
f(x)=a^x
\end{equation*}
y cumple con las siguientes propiedades.
Sean \(a,b \in\mathbb{R}^+\) y \(x, y,\in \mathbb{R}.\) Entonces
- \(a^0=1\)
- \(a^{(x+y)}=a^xa^y\)
- \(\frac{a^x}{a^y}=a^{x-y} \)
- \(a^{yx}=(a^x)^y = (a^y)^x\)
- \(a^{-x}=\frac{1}{a^x} \)
- \((ab)^x=a^xb^x\)
- \((\frac{a}{b})^x=\frac{a^x}{b^x} \)
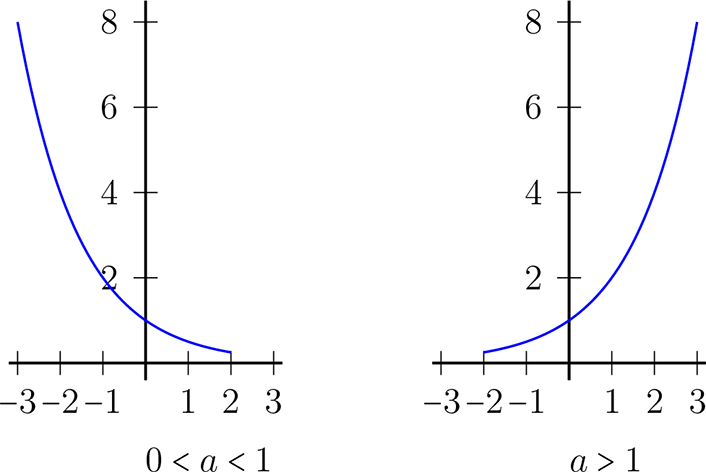
Si \(0 \lt a \lt 1\) entonces \(f(x)=a^x\) es una función decreciente.
Si \(a \gt 1\) entonces \(f(x)=a^x\) es una función creciente
Definición 3.7.2
Para cada \(a\in \mathbb{R}^+\text{,}\) la función
\begin{equation*}
\begin{array}[t]{rl}
\exp_a : \mathbb{R} \amp \longrightarrow \mathbb{R}^+\\
x \amp \longmapsto a^x \\
\end{array}
\end{equation*}
se llama función exponencial en base \(a.\)
Su gráfica es la siguiente:
Ejemplo 3.7.3
Algunos ejemplos numéricos
- \((3^3)(3^4)=3^{3+4}=3^7\)
- \(\frac{2^5}{2^3}=2^{5-3}=2^2\)
- \(\frac{2^3}{2^5}=2^{3-5}=2^{-2}=\frac{1}{2^2} \)
- \((3^x)^4=3^{4x} \)
- \((\frac{1}{3})^{-x}=(3^{-1})^{-x}=3^x\)
Subsección 3.7.1 Funciones Logarítmicas
¶
Teorema 3.7.4
Sea \(a\in\mathbb{R}^{+}-\{1\}\) entonces la función exponencial en base \(a\) es biyectiva, por lo tanto existe la función inversa.
Definición 3.7.5
La función inversa de la exponencial en base \(a\) se llama función logaritmo en base \(a\) y la denotaremos como \(\log_a\text{,}\) es decir:
\begin{equation*}
\log_a x = y\Longleftrightarrow \exp_a(y)=x
\end{equation*}
Si \(a\in\mathbb{R}^{+}-\{1\}\) podemos definir la función como:
\begin{equation*}
\begin{array}{rl}
\log_a : \amp \mathbb{R}^+\longrightarrow \mathbb{R}\\
\amp x \longmapsto \log_a(x)=y
\end{array}
\end{equation*}
Las Gráfica correspondiente son:
Ejemplo 3.7.6
De algunos cálculos numéricos
\(\log_{10} 10^3=3\text{,}\) pues \(10^3=1000\)
\(\log_2 1 = 0\text{,}\) pues \(2^0=1\)
Proposición 3.7.7
Sean \(a\in\mathbb{R}^+-\{1\}, x,y\in\mathbb{R}^+,r\in \mathbb{R} \) entonces
- \(\log_a(xy)=\log_a x+\log_a y\)
- \(\log_a\left(\frac{x}{y}\right)=\log_a x -\log_a y\)
- \(\log_a(x^r)=r\log_a x\)
- \(\log_a(1)=0\)
- \(\log_a(a^r)=r\)
- \(\log_a(x)=\log_a(y)\Longleftrightarrow x=y\)
Si \(0 \lt a \lt 1\) entonces \(\log_a\) es una función decreciente.
Si \(a \gt 1\) entonces \(\log_a\) es una función creciente.
Demostración
Sea \(u=\log_a x\) y \(v=\log_a y\) entonces \(a^u=x\) y \(a^v=y\)
Para (1) tenemos que
\begin{equation*}
\log_a(xy)=\log_a(a^u a^v)=\log_a a^{u+v}=u+v
\end{equation*}
Luego
\begin{equation*}
\log_a(xy)=\log_a x+\log_a y
\end{equation*}
En (2)
\begin{equation*}
\log_a\left(\frac{x}{y}\right)=\log_a(a^u a^{-v})=\log_a a^{u-v}=u-v
\end{equation*}
\begin{equation*}
\log_a\left(\frac{x}{y}\right)=\log_a x - \log_a y
\end{equation*}
En (3)
\begin{equation*}
\log_a x^r=\log_a(a^u)^r=\log_a a^{ru}=ru
\end{equation*}
\begin{equation*}
\log_a x^r=r\log_a x
\end{equation*}
Las propiedades siguientes quedan como tarea para el lector.
Ejemplo 3.7.8
- \(\log_{10} x^2y=2\log_{10} x+\log_{10} y\)
- \(\log_2\frac{1}{x}=\log_2 x^{-1}=-\log_2 x\)
Teorema 3.7.9 [Cambio de Base]
Sean \(a,b\in\mathbb{R}^+-\{1\},x\in\mathbb{R}\text{,}\) entonces
\begin{equation*}
\log_b x=\frac{\log_a x}{\log_a b}
\end{equation*}
Demostración
Sea \(u=\log_a x,v=\log_b x\text{,}\) entonces \(a^u=x\) y \(b^v=x\) así tenemos que
\begin{equation*}
\begin{array}{rcl}
a^u \amp = \amp b^v\\
\log_a a^u \amp = \amp \log_a b^v\\
u \amp = \amp v\log_a b\\
\log_a x \amp = \amp \log_b x\log_a b\\
\log_b x \amp = \amp \frac{\log_a x}{\log_a b}
\end{array}
\end{equation*}
Ejemplo 3.7.10
Resolver la siguientes ecuaciones
- \(y=\log_2 8.\)
Luego \(2^y=8\text{,}\) por lo tanto \(y=3\text{.}\)
-
\(\log_a \frac{1}{16}=4\text{.}\)
Lo cual significa que \(a^4=\frac{1}{16}\text{,}\) de este modo se tiene \(a=\frac{1}{2}\)
-
\(\log_a x=-2\text{.}\)
Traduciendo tenemos \(3^{-2}=y\text{,}\) luego \(\frac{1}{9}=y\text{.}\)
Subsección 3.7.2 Ecuaciones Exponenciales y Logarítmicas
¶Una ecuación que contiene una o más funciones logarítmicas con una o más incógnitas se llama ecuación logarítmica. Análogamente para las ecuaciones exponenciales.
Ejemplo 3.7.11
Resolver la ecuación
\begin{equation*}
\log (x-2)+\log(x+1)+1=\log 40
\end{equation*}
Primeros veremos la restricción, esta son,
\begin{equation*}
x-2 \gt 0 \wedge x+1 \gt 0
\end{equation*}
Entonces \(\mathcal{R}=[2,+\infty[\)
Ahora despejemos la variable, teniendo presente las propiedades de logaritmo
\begin{equation*}
\begin{array}{rcl}
\log (x-2)+\log(x+1)+1 \amp = \amp \log 40\\
\log (x-2)+\log(x+1)+\log 10 \amp = \amp \log 40\\
\log (x-2)(x+1)10 \amp = \amp \log 40\\
(x-2)(x+1)10 \amp = \amp 40\\
(x-2)(x+1) \amp = \amp 4\\
x^2-x-6 \amp = \amp 0\\
(x+2)(x-3) \amp = \amp 0\\
x=-2 \amp \vee \amp x=3
\end{array}
\end{equation*}
pero \(x=-2\text{,}\) por restricción no es admisible. Por lo tanto el conjunto solución es \(\{3\}\text{.}\)
Ejemplo 3.7.12
Resolver la ecuación
\begin{equation*}
\log 2+\log (4^{x-2}+9)=1+\log
(2^{x-2}+1)
\end{equation*}
Veamos el conjunto restricción
\begin{equation*}
4^{x-2} + 9 \gt 0 \wedge 2^{x-2}+1 \gt 0
\end{equation*}
Entonces \(\mathcal{R}=\mathbb{R}\text{.}\)
Luego resolviendo la ecuación nos queda
\begin{equation*}
\begin{array}{rcl}
\log 2+\log (4^{x-2}+9) \amp = \amp 1+\log (2^{x-2}+1)\\
\log 2(4^{x-2}+9) \amp = \amp \log 10(2^{x-2}+1)\\
2(4^{x-2}+9) \amp = \amp 10(2^{x-2}+1)\\
2^{2x}-20\cdot2^{x}+64 \amp = \amp 0
\end{array}
\end{equation*}
Consideremos la variable auxiliar \(u=2^x\text{,}\) reemplazando obtenemos la ecuación cuadrática.
\begin{equation*}
\begin{array}{rcl}
u^2- 20u+64 \amp = \amp 0\\
(u - 16)(u - 4)\amp = \amp 0\\
u=16 \amp \vee \amp u=4\\
2^x = 16 \amp \vee \amp 2^x=4\\
x=4 \amp \vee \amp x=2
\end{array}
\end{equation*}
Luego el conjunto solución de la ecuación es \(\{2,4\}\)
Subsección 3.7.3 Inecuaciones Exponenciales y Logarítmicas
¶Debemos tener presente que para resolver inecuaciones con logaritmo o exponenciales es importante recordar que cuando la base es menor que 1, exponencial y logaritmo son decreciente y en el caso que la base sea mayor que 1, se tiene que es creciente.
Ejemplo 3.7.13
Resolver la inecuación
\begin{equation*}
\log_\frac{1}{2}(x^2 - 1)\leq 2
\end{equation*}
Primero veremos la Restricciones
\begin{equation*}
x^2 - 1 \gt 0
\end{equation*}
\begin{equation*}
(x+1)(x-1) \gt 0
\end{equation*}
Por lo tanto
\begin{equation*}
x\in ]-\infty,-1[ \cup ]1,+\infty[=\mathcal{R}
\end{equation*}
Veremos los elementos que la satisface
\begin{equation*}
\begin{array}{lrl}
\amp \log_\frac{1}{2}(x^2 - 1) \amp \leq 2 \ / \exp_\frac{1}{2} \downarrow \\
\amp x^2 - 1 \amp \geq \frac{1}{4}\\
\amp x^2 - \frac{5}{4} \amp \geq 0 \\
\amp (x-\frac{\sqrt{5}}{2})(x+ \frac{\sqrt{5}}{2}) \amp \geq 0 \\
\end{array}
\end{equation*}
\begin{equation*}
x\in \left]-\infty,-\frac{ \sqrt{5}}{2}\right[ \cup \left]\frac{\sqrt{5}}{2},+\infty
\right[=S_1
\end{equation*}
Luego la solución de la inecuación es:
\begin{equation*}
S = \mathcal{R} \cap S_1
\end{equation*}
\begin{equation*}
x\in \left]-\infty,\frac{-\sqrt{5}}{2}\right[ \cup \left]\frac{\sqrt{5}}{2},
+\infty\right[
\end{equation*}
Ejemplo 3.7.14
Resuelva la siguiente inecuación
\begin{equation*}
\log_{\frac{1}{3}}(\log_5
(x^2-4) \gt -2
\end{equation*}
El conjunto restricción para la inecuación cumple con:
\begin{equation*}
\begin{array}{rcl}
x^2-4 \gt 0 \amp \wedge \amp \log_5 (x^2-4) \gt 0\\
x^2 \gt 4 \amp \wedge \amp x^2-4 \gt 1\\
|x| \gt 2 \amp \wedge \amp |x| \gt \sqrt{5}\\
\end{array}
\end{equation*}
Luego \(x\in ]-\infty,-\sqrt{5}[\cup]\sqrt{5},+\infty[=\mathcal{R}.\)
Ahora resolvamos la inecuación,
\begin{equation*}
\begin{array}{rcl}
\log_{\frac{1}{3}}(\log_5 (x^2-4) \amp \gt \amp -2\ / \exp_\frac{1}{3} \downarrow \\
\log_{5}(x^2-4) \amp \lt \amp (\frac{1}{3})^{-2}\ / \exp_5 \uparrow \\
x^2-4 \amp \lt \amp 5^9\\
|x| \amp \lt \amp \sqrt{5^9+4}\\
-\sqrt{5^9+4} \amp \lt x \lt \amp \sqrt{5^9 +4}
\end{array}
\end{equation*}
Luego el conjunto solución es:
\begin{equation*}
S=]-\sqrt{5^9+4},\sqrt{5^9+4}[ \cap\mathcal{R}= ]-\sqrt{5^9+4},-\sqrt{5}[\cup
]\sqrt{5},\sqrt{5^9+4}[.
\end{equation*}
Ejemplo 3.7.15
Resolver la inecuación
\begin{equation*}
\log_{3x} (9x)+\log_3(x^3)\leq 2
\end{equation*}
El conjunto restricción de la inecuación es \(\mathbb{R}^+ -\{\frac{1}{3}\}\)
\begin{equation*}
\begin{array}{rcl}
\log_{3x} (9x)+\log_3(x^3)\amp \leq \amp 2\\
\frac{\log_3 (9x)}{\log_3(3x)} + \log_3(x^3) \amp \leq \amp 2\\
\frac{\log_3 9+\log_3 x}{\log_3 3 +\log_3 x} + 3\log_3(x) \amp \leq \amp 2\\
\end{array}
\end{equation*}
Sea \(u=\log_3 x\) entonces
\begin{equation*}
\begin{array}{rcl}
\frac{2+u}{1+u}+3u \amp \leq \amp 2\\
\frac{2u+3u^2}{1+u} \amp \leq \amp 0\\
\frac{u(2+3u)}{1+u} \amp \leq \amp 0
\end{array}
\end{equation*}
Resumamos en una tabla
\begin{equation*}
\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
\amp \amp -1 \amp \amp -2/3\amp \amp 0 \amp \\ \hline
1+u \amp - \amp 0 \amp + \amp \amp + \amp \amp + \\ \hline
u \amp - \amp \amp - \amp \amp - \amp 0 \amp + \\ \hline
2+3u \amp - \amp \amp - \amp 0 \amp + \amp \amp + \\ \hline
\amp - \amp \amp + \amp \amp - \amp \amp + \\ \hline
\end{array}
\end{equation*}
Luego tenemos \(u\leq-1\ \vee - \frac{2}{3}\leq u \leq 0 \text{,}\) reemplazando
\begin{equation*}
\begin{array}{rcl}
\log_3 x \leq-1 \amp \vee \amp -\frac{2}{3}\leq \log_3 x \leq 0 \ / \exp_3 \uparrow \\
x\leq 3^{-1} \amp \vee \amp 3^{-\frac{2}{3}}\leq x \leq 1
\end{array}
\end{equation*}
Pero, por restricción tenemos que \(x \gt 0\) y \(x\not = \frac{1}{3}\) entonces
\begin{equation*}
0 \lt x \lt \frac{1}{3} \ \ \vee \ \ \frac{1}{\sqrt[3]{3^2}} \leq x \leq 1
\end{equation*}
El conjunto solución es
\begin{equation*}
S=\left]0,\frac{1}{3}\right[\cup\left[\frac{1}{\sqrt[3]{3^2}},1\right]
\end{equation*}
Subsección 3.7.4 Ejercicios Propuestos
¶
-
Exprese como un solo logaritmo.
- \(\frac{1}{3}\log \frac{1}{3}+\frac{1}{5}\log\frac{1}{2}-\log{1}{5}\)
- \(1+\log_3 a+\frac{1}{2}\log_3 a^3-4\log_3 a^6\)
- \(2\log y-\frac{1}{4}\log(c-x)+\frac{1}{2}\log(x-2y+c)\)
-
Resolver las siguientes ecuaciones.
- \(7^{2x}-7^{x+1}-8=0\)
- \(2^{2x+1}+2^{x+3}=10\)
- \(5^{2x+2} +1=(10+5^{x})5^x\)
- \(\dfrac{10^{x}-10^{-x}}{10^x+10^{-x}}=\frac{1}{3}\)
- \(\left(\dfrac{4}{9}\right)^x \left(\dfrac{27}{8}\right)^{(x-1)}=\dfrac{\log 4}{\log 8}\)
- \(\log x^5+\log^2 x+6=0\)
- \((\log_2 x)(\log_2 x+1)=2\)
- \(\log(7x-9)^2+\log(3x-4)^2=2\)
- \(3\log_5 x-\log_5 32=2\log_{25} (\frac{x}{2})\)
- \(\log_5 (5^x-7)-\log_{25} 324=2-x\)
- \(\log \sqrt{7-x})=\log \sqrt{ \log(100)+10}- \log\sqrt{x+1}\)
- \(\log_\frac{1}{2} (\log_{4}(|x|-1)=2\)
- \(\log_{1/3} (x)+\log_{9}(x) =1\)
- \(\log_x(5x^2)(\log_5 x)^2=1\)
-
Resolver las siguientes ecuaciones.
- \(a^{x^2}a^x=a^{3x+1} \) con \(a \neq 1, a\in \mathbb{R}^+\)
- \(a^{x^2+2x}=a^{6x-3} \) con \(a\in ]1, \infty [\)
- \(b^{5x-6}=b^{x^2}\) con \(b\in ]0,1 [\)
- \(\dfrac{\log_2 x}{(\log_2 a)^2}-\dfrac{2\log_a x}{\log_{1/2} a } = (\log_{\sqrt[3]{a}} x)( \log_a x) \) con \(a \neq 1, a\in \mathbb{R}^+\)
- \(\dfrac{\log_{4\sqrt{x}}2}{\log_{2x} 2} +(\log_{2x} 2)(\log_{1/2} 2x) = 0\)
-
Resolver las siguientes inecuaciones.
- \(\log_{\frac{1}{2}}(x^2-1)\leq 2\)
- \(\log_3(x^2-3x-4) \lt 1\)
- \(\log_{\frac{x}{3}}(x(4-x))\leq 1\)
- \(\log_4x+\log_4(x+1) \lt \log_4(2x+6)\)
- \(\log_{1/2}x+\log_{1/2}(2x) \gt 1\)
- \(\dfrac{\log_2 (x-\frac{1}{2})}{\log_2 x} \lt 2\)
- \(\log_9(\log_\frac{1}{2} (x^2-1)-\log_\frac{1}{2} (x+1)) \lt 0\)
- \(7^{2x}-7^{x+1}-8\leq 0\)
- \(\log_2(\log_{\frac{1}{2}}(x+1)) \gt 1\)
- \(\log_\frac{1}{2} (\log_{4}(|x|-1) \lt 2\)
- \(\log_x (3x-5) \lt 2\)
- \(\log_x (3x+5) \leq 2\)
- \(\log_{x+3} (x^2-x) \lt 2\)
-
Hallar la función inversa de
\begin{equation*}
y=\log_b x-\log_b (1+x),\quad b \gt 0
\end{equation*}
-
Demostrar que
\begin{equation*}
\log_b(\sqrt{x+2}-\sqrt{x+1})=-\log_b(\sqrt{x+2}+\sqrt{x+1})
\end{equation*}
-
Resolver el sistema
\begin{equation*}
\begin{array}{rcl|}
\log_{12}x\left( \dfrac{1}{\log_x 2} + \log_2 y \right) \amp = \amp \log_2 x \\
\log_{2}x \log_3 (x+y) \amp = \amp 3\log_3 x \\ \hline
\end{array}
\end{equation*}