Sección 2.7 Hipérbola
¶
Definición 2.7.1
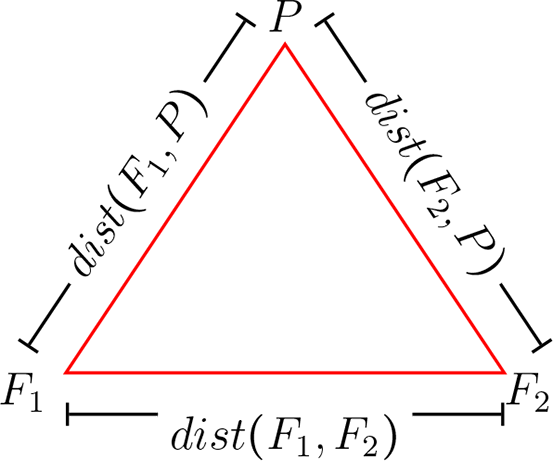
Una hipérbola es una figura geométrica plano y corresponde al conjunto de todos los puntos que se encuentran en el plano tales que el valor absoluto de la diferencia de las distancias a dos puntos fijos es constante, los puntos fijos se llaman focos.
Sean \(F_{1}, F_{2} \in \mathbb{R}^{2}\) donde \(F_{1}\) y \(F_{2}\) son puntos fijos en el plano que denotaremos como focos y \(P \in
\mathbb{R}^{2}\) un punto que satisface la definición de la hipérbola
entonces consideremos las distancias que hay entre estos \(3\) puntos
Como \(P\) satisface la definición de la hipérbola tenemos
\begin{equation*}
\begin{array}{rcl}
\mid dist(P,F_{1}) - dist(P,F_{2}) \mid = r
\end{array}
\end{equation*}
Luego \(\mathcal{H}_{F_{1},F_{2}}\) representa al conjunto de todos los puntos que pertenecen a la hipérbola, es decir,
\begin{equation*}
\begin{array}{rcl}
\mathcal{H}_{F_{1},F_{2}} = \{ P \in \mathbb{R}^{2} \;\;\; \mid \;\;
\mid dist(P,F_{1}) - dist(P,F_{2}) \mid =r \}
\end{array}
\end{equation*}
Subsección 2.7.1 Ecuación de la hipérbola con eje focal paralelo al eje \(X\)
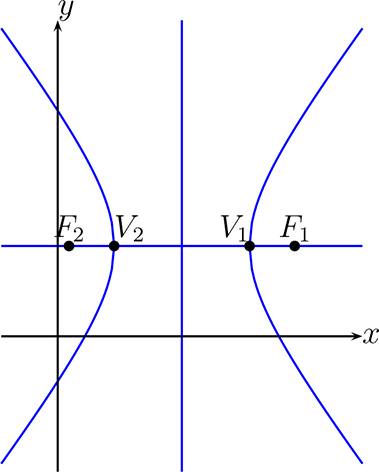
¶Sean \(V_{1},V_{2},F_{1},F_{2} \in \mathbb{R}^{2}\) y \(P \in
\mathcal{H}_{F_{1}, F_{2}} \text{,}\) donde \(V_{1} , V_{2}\) representan los vertices de la hipérbola, \(F_{1}\) y \(F_{2}\) los focos y \(P =
(x,y)\) un punto cualquiera que pertenece a la hipérbola.
Sea \(C=(h,k)\) el centro entonces los focos para nuestro caso están dados por:
\begin{equation*}
F_{1} = (h-c, k) \ \ \ y \ \ \ F_{2} = (h+c,k)
\end{equation*}
luego
\begin{equation*}
\begin{array}{rcl}
\mid dist(P,F_{1}) - dist(P,F_{2}) \mid \amp =\amp 2a \\
\mid \sqrt{(x-h+c)^{2} + (y-k)^{2}} - \sqrt{(x-h-c)^{2}+ (y-k)^{2}}
\mid \amp =\amp 2a
\end{array}
\end{equation*}
usando el cambio de variable \(u = x - h \) y \(v= y - k\)
\begin{equation*}
\begin{array}{rcl}
\mid \sqrt{(x-h+c)^{2} + (y-k)^{2}} - \sqrt{(x-h-c)^{2}+ (y-k)^{2}}
\mid \amp =\amp 2a\\
\mid \sqrt{(u+c)^{2} + v^{2}} - \sqrt{(u-c)^{2} + v^{2}} \mid \amp =\amp 2a
\end{array}
\end{equation*}
De lo cual obtenemos los siguientes casos
\begin{equation*}
\sqrt{(u+c)^{2} + v^{2}} - \sqrt{(u-c)^{2} + v^{2}} = 2a
\end{equation*}
\begin{equation*}
\sqrt{(u+c)^{2} + v^{2}} - \sqrt{(u-c)^{2} +
v^{2}} = - 2a
\end{equation*}
Si \(P\) está en la parte izquierda de los focos tenemos que la primera ecuación es verdadero y si \(P\) se encuentra en la parte derecha de los focos tenemos que la segunda ecuación es verdadero, luego podemos trabajar las dos ecuaciones del siguiente modo
\begin{equation*}
\begin{array}{rcl}
\sqrt{(u\pm c)^{2} + v^{2}} - \sqrt{(u\mp c)^{2} + v^{2}} \amp =\amp 2a \ \ \ \ (*) \\
\sqrt{(x \pm c)^{2} + y^{2}} \amp =\amp 2a + \sqrt{(u \mp c)^{2} + y^{2}} \hspace{0.5cm} /()^{2} \\
(u \pm c)^{2} + v^{2} \amp =\amp (2a + \sqrt{(u \mp c)^{2} + y^{2}})^{2} \\
u^{2} \pm 2uc +c^{2} + v^{2} \amp =\amp 4a^{2} + 4a \sqrt{(u \mp c)^{2} + v^{2}} + (u \mp c)^{2} + v^{2} \\
u^{2} \pm 2uc +c^{2} + v^{2} \amp =\amp 4a^{2} + 4a \sqrt{(u \mp c)^{2} + v^{2}} + u^{2} \mp 2uc+c^{2} + v^{2} \\
\pm 4uc -4a^{2} \amp =\amp 4a \sqrt{(u \mp c)^{2} + v^{2}} \ \ \ \ \ / \frac{1}{4} \\
\pm uc - a^{2} \amp =\amp a \sqrt{(u \mp c)^{2} + v^{2}} \ \ \ \ \ /()^{2}
\end{array}
\end{equation*}
Antes veremos la restricción
\begin{equation*}
\begin{array}{rcl}
\pm uc - a^{2} \geq 0 \\
uc - a^{2} \geq 0 \amp \vee \amp -uc - a^{2} \geq 0 \\
u \geq \frac{a^{2}}{c} \amp \vee \amp u \leq -\frac{a^{2}}{c}
\end{array}
\end{equation*}
luego es un semiplano en cada caso. Además como \(2a \lt 2c\)
\begin{equation*}
\begin{array}{rcl}
u^{2}c^{2} \mp 2a^{2}uc + a^{4} \amp =\amp a^{2} ((u \mp c)^{2} + v^{2}) \\
u^{2}c^{2} \mp 2a^{2}uc + a^{4} \amp =\amp a^{2} (u^{2} \mp 2uc +c^{2} + v^{2}) \\
u^{2}c^{2} \mp 2a^{2}uc + a^{4} \amp =\amp a^{2} u^{2} \mp 2a^{2}uc +a^{2}c^{2} + a^{2}v^{2} \\
u^{2}(c^{2} - a^{2}) - a^{2}v^{2} \amp =\amp a^{2} (c^{2} - a^{2})
\end{array}
\end{equation*}
Como \(2a \lt 2c\) entonces \(a^{2} \lt c^{2}\text{,}\) es decir, \(c^{2} - a^{2} \gt 0\text{.}\)
Por lo tanto, sea \(b^{2} \) tal que
\begin{equation*}
b^{2} = c^{2} - a^{2} \gt 0
\end{equation*}
Reemplazando en la ecuación, obtenemos
\begin{equation*}
\begin{array}{rcl}
u^{2}(c^{2} - a^{2}) - a^{2}v^{2} \amp =\amp a^{2} (c^{2} - a^{2}) \\
u^{2}b^{2} - a^{2}v^{2} \amp =\amp a^{2} b^{2} \hspace{0.5cm} /\frac{1}{a^{2}b^{2}} \\
\frac{u^{2}}{a^{2}} - \frac{v^{2}}{b^{2}} \amp =\amp 1
\end{array}
\end{equation*}
volviendo a las variables originales obtenemos
\begin{equation*}
\frac{(x-h)^{2}}{a^{2}} - \frac{ (y-k)^{2}}{b^{2}} = 1
\end{equation*}
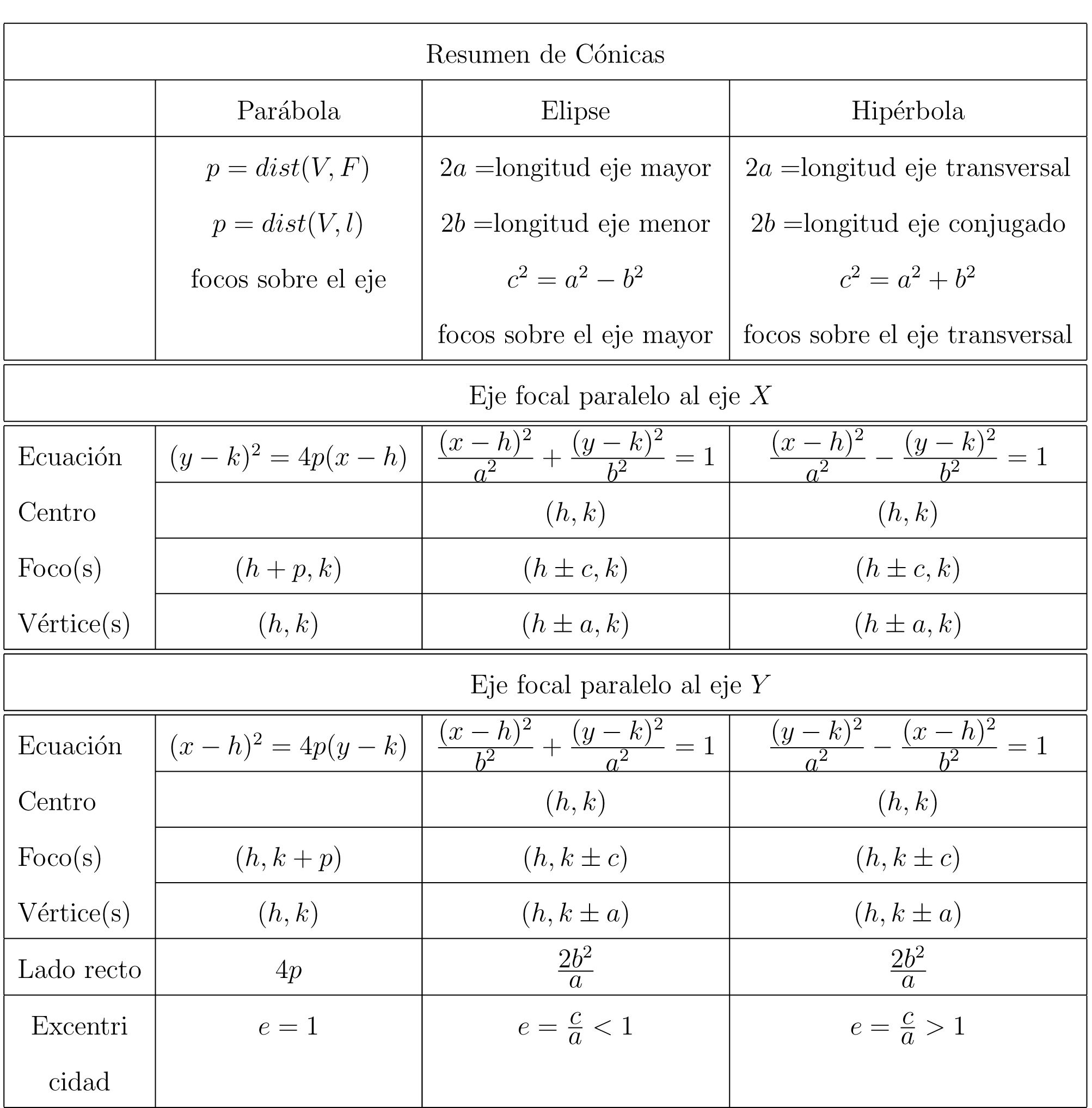
Proposición 2.7.2
Sea \(V_{1},V_{2},C,F_{1},F_{2} \in \mathbb{R}^{2}\) y \(P \in
\mathcal{H}_{F_{1}, F_{2}} \text{,}\) con \(C = (h,k)\) el centro de la hipérbola, \(F_{1} = (h-c,k)\) y \(F_{2}= (h+c,k)\) los focos, los vértices son \(V_{1} = (h-a,k)\) y \(V_{2}= (h+a,k)\) y \(P = (x,y)\) pertenece a la hipérbola si sólo si satisface la ecuación
\begin{equation*}
\frac{(x-h)^{2}}{a^{2} } - \frac{ (y-k)^{2}}{b^{2}} = 1, \text{ donde } b^2=c^2-a^2
\end{equation*}
Ejemplo 2.7.3
Encuentre la ecuación de la hipérbola que tiene su centro en el origen, un foco \(F_{1}=(5,0)\text{,}\) el valor de \(a=2\) y el eje focal en el eje \(X\text{.}\)
Como el centro de la hipérbola es \(C=(0,0)\) y \(F_{1}=(5,0)\) tenemos \(dist(C,F_{1})=c\) entonces
\begin{equation*}
dist(C,F_{1})= \sqrt{(5-0)^{2}+(0-0)^{2}} = 5
\end{equation*}
Ya que \(c=5\text{,}\) luego el valor de \(b\) está dado por:
\begin{equation*}
\begin{array}{rcl}
c^{2} \amp =\amp b^{2} +a^{2} \\
5^{2} \amp =\amp b^{2}+2^{2}\\
b^{2} \amp =\amp 21
\end{array}
\end{equation*}
Por lo tanto la ecuación de la hipérbola es:
\begin{equation*}
\begin{array}{rcl}
\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} \amp =\amp 1 \\
\frac{x^{2}}{4} - \frac{y^{2}}{25} \amp =\amp 1.
\end{array}
\end{equation*}
Ejemplo 2.7.4
Encuentre la ecuación de la hipérbola que tiene su centro en el punto \(C=(4,3)\text{,}\) un foco \(F_{1}=(8,3)\text{,}\) el valor de \(a=2\) y el eje focal paralelo al eje \(X\text{.}\)
Como el centro de la hipérbola es \(C=(4,3)\) y \(F_{1}=(8,3)\) tenemos \(dist(C,F_{1})=c\) entonces
\begin{equation*}
\begin{array}{rcl}
dist(C,F_{1})\amp =\amp \sqrt{(8-4)^{2}+(3-3)^{2}}= \sqrt{(4)^{2}} = 4
\end{array}
\end{equation*}
Ya que \(c=4\text{,}\) luego el valor de \(b\) está dado por:
\begin{equation*}
\begin{array}{rcl}
c^{2} \amp =\amp b^{2} +a^{2} \\
b^{2} \amp =\amp 12
\end{array}
\end{equation*}
Por lo tanto la ecuación de la hipérbola es:
\begin{equation*}
\begin{array}{rcl}
\frac{(x-4)^{2}}{a^{2}} - \frac{(y-3)^{2}}{b^{2}} \amp =\amp 1 \\
\frac{(x-4)^{2}}{4} - \frac{(y-3)^{2}}{144} \amp =\amp 1.
\end{array}
\end{equation*}
Subsección 2.7.2 Ecuación de la hipérbola con eje focal paralelo al eje \(Y\)
¶Sea \(V_{1},V_{2},C,F_{1},F_{2} \in \mathbb{R}^{2}\text{,}\) con \(F_{1}\) y \(F_{2}\) los focos de la hipérbola, \(V_{1},V_{2}\) los vértices y \(P = (x,y)\) un punto cualquiera que pertenece a la hipérbola.
Sea \(C=(h,k)\) el centro de la hipérbola entonces los focos para nuestro caso son \(F_{1}=(h,k-c) \) y \(F_{2}=(h,k+c)\) luego,
\begin{equation*}
\begin{array}{rcl}
\mid dist(P,F_{1}) - dist(P,F_{2}) \mid \amp =\amp 2a \\
\mid \sqrt{(x-h)^{2} +(y-k+c)^{2}} - \sqrt{(x-h)^{2}+(y-k-c)^{2}}\mid \amp =\amp 2a
\end{array}
\end{equation*}
usando el cambio de variable
\begin{equation*}
v = x - h \ \ \ \text{ y }\ \ \ u = y - k
\end{equation*}
\begin{equation*}
\begin{array}{rcl}
\mid \sqrt{(x-h)^{2} +(y-k+c)^{2}} - \sqrt{(x-h)^{2}+(y-k-c)^{2}} \mid \amp =\amp 2a \\
\mid \sqrt{(v)^{2} +(u+c)^{2}} - \sqrt{(v)^{2}+(u-c)^{2}} \mid \amp =\amp 2a
\end{array}
\end{equation*}
Y es un expresión igual a la obtenida en el sección anterior, luego usando el mismo desarrollo tenemos
\begin{equation*}
\begin{array}{rcl}
\frac{u^{2}}{a^{2} } \amp -\amp \frac{ v^{2}}{b^{2}} = 1
\end{array}
\end{equation*}
volviendo a las variables originales obtenemos
\begin{equation*}
\begin{array}{rcl}
\frac{(y-k)^{2}}{a^{2} } \amp -\amp \frac{ (x-h)^{2}}{b^{2}} = 1
\end{array}
\end{equation*}
Proposición 2.7.5
Sea \(V_{1},V_{2},C,F_{1},F_{2} \in \mathbb{R}^{2}\) con \(C = (h,k)\) el centro de la hipérbola, \(F_{1} = (h,k-c)\) y \(F_{2}= (h,k+c)\) los focos, los vértices \(F_{1} = (h,k-a)\) y \(F_{2}= (h,k+a)\) \(P = (x,y)\) pertenece a la hipérbola si y sólo si satisface la ecuación
\begin{equation*}
\frac{(y-k)^{2}}{a^{2} } - \frac{ (x-h)^{2}}{b^{2}} = 1 \text{ donde } b^2=c^2-a^2
\end{equation*}
Ejemplo 2.7.6
Encuentre la ecuación de la hipérbola que tiene su centro en el origen, un foco \(F_{1}=(0,7)\text{,}\) el valor de \(a=3\) y el eje focal en el eje \(Y\text{.}\)
Como el centro de la hipérbola es \(C=(0,0)\) y \(F_{1}=(0,7)\) tenemos \(dist(C,F_{1})=c\) entonces
\begin{equation*}
\begin{array}{rcl}
dist(C,F_{1})\amp =\amp \sqrt{(0-0)^{2}+(7-0)^{2}} = \sqrt{(7)^{2}} = 7
\end{array}
\end{equation*}
Ya que \(c=7\text{,}\) luego el valor de \(b\) está dado por:
\begin{equation*}
\begin{array}{rcl}
c^{2} \amp =\amp b^{2} +a^{2} \\
7^{2} \amp =\amp b^{2}+3^{2}\\
b^{2} \amp =\amp 40
\end{array}
\end{equation*}
Por lo tanto la ecuación de la hipérbola es:
\begin{equation*}
\begin{array}{rcl}
\frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}} \amp =\amp 1 \\
\frac{y^{2}}{9} - \frac{x^{2}}{49} \amp =\amp 1.
\end{array}
\end{equation*}
Ejemplo 2.7.7
Encuentre la ecuación de la hipérbola que tiene su centro en el punto \(C=(5,9)\text{,}\) un foco \(F_{1}=(5,16)\text{,}\) el valor de \(a=3\) y el eje focal en el eje \(Y\text{.}\)
Como el centro de la hipérbola es \(C=(5,9)\) y \(F_{1}=(5,16)\) tenemos \(dist(C,F_{1})=c\) entonces
\begin{equation*}
\begin{array}{rcl}
dist(C,F_{1})\amp =\amp \sqrt{(5-5)^{2}+(16-9)^{2}} = \sqrt{(7)^{2}} = 7
\end{array}
\end{equation*}
Ya que \(c=7\text{,}\) luego el valor de \(b\) está dado por:
\begin{equation*}
\begin{array}{rcl}
c^{2} \amp =\amp b^{2} +a^{2} \\
7^{2} \amp =\amp b^{2}+3^{2}\\
b^{2} \amp =\amp 40
\end{array}
\end{equation*}
Por lo tanto la ecuación de la hipérbola es:
\begin{equation*}
\begin{array}{rcl}
\frac{(y-9)^{2}}{a^{2}} - \frac{(x-5)^{2}}{b^{2}} \amp =\amp 1 \\
\frac{(y-9)^{2}}{9} - \frac{(x-5)^{2}}{49} \amp =\amp 1.
\end{array}
\end{equation*}
Observación: Sea \(V_{1},V_{2},C,F_{1},F_{2} \in
\mathbb{R}^{2}\) y \(P \in \mathcal{H}_{F_{1}, F_{2}} \text{,}\) con \(C =
(h,k)\) el centro de la hipérbola , \(F_{1}\) y \(F_{2}\) los focos
Consideremos la ecuación de la hipérbola donde el eje focal es paralelo al eje \(X\)
\begin{equation*}
\frac{(x-h)^{2}}{a^{2} } - \frac{ (y-k)^{2}}{b^{2}} = 1
\end{equation*}
Desarrollemos la ecuación
\begin{equation*}
\begin{array}{rcl}
\frac{(x-h)^{2}}{a^{2} } - \frac{ (y-k)^{2}}{b^{2}} \amp =\amp 1 \ \ /(a^{2}b^{2}) \\
b^{2}[(x-h)^{2}] - a^{2} [(y-k)^{2}] \amp =\amp a^{2} b^{2} \\
b^{2}[x^{2} - 2xh + h^{2}] - a^{2}[y^{2} - 2yk + k^{2}] \amp =\amp a^{2}b^{2} \\
x^{2}b^{2} - 2xhb^{2} + h^{2}b^{2} - y^{2}a^{2} + 2yka^{2} - k^{2}a^{2} \amp =\amp a^{2}b^{2} \\
x^{2}b^{2} - 2xhb^{2} - y^{2}a^{2} + 2yka^{2} - k^{2}a^{2} +
h^{2}b^{2} - a^{2}b^{2} \amp =\amp 0
\end{array}
\end{equation*}
Se define las constantes \(A_{1},B_{1},C_{1},D_{1},E_{1} \in \mathbb{R}\) tales que
\begin{equation*}
\begin{array}{rcl}
A_{1} = b^{2}; \ \
B_{1} = -2hb^{2}; \ \
C_{1} = -a^{2}; \ \
D_{1} = 2ka^{2}; \ \
E_{1} = -k^{2}a^{2} + h^{2}b^{2} - a^{2}b^{2}.
\end{array}
\end{equation*}
\begin{equation*}
A_1x^{2} +B_1x +C_1y^{2} + D_1y +E_1=0
\end{equation*}
Análogamente para la otra ecuación
\begin{equation*}
\begin{array}{rcl} \frac{(y-k)^{2}}{a^{2} } -
\frac{ (x-h)^{2}}{b^{2}} = 1
\end{array}
\end{equation*}
podemos transformarla
\begin{equation*}
A_2y^{2} +B_2y +C_2x^{2} + D_2x +E_2=0
\end{equation*}
Con
\begin{equation*}
\begin{array}{rcl}
A_{2} = b^{2}; \ \
B_{2} = -2kb^{2}; \ \
C_{2} = -a^{2}; \ \
D_{2} = -2kb^{2}; \ \
E_{2} = -k^{2}b^{2} + h^{2}a^{2} - a^{2}b^{2}.
\end{array}
\end{equation*}
Proposición 2.7.8
Sean \(A,C \in \mathbb{R}^{\ast}, B,D,E \in \mathbb{R}\) la ecuación
\begin{equation*}
\begin{array}{rcl}
Ax^{2} + Bx + Cy^{2} + Dy + E \amp =\amp 0
\end{array}
\end{equation*}
define una hipérbola si y sólo si
\begin{equation*}
\begin{array}{rcl}
AC \lt 0 \land CB^{2}+AD^{2}-4ACE \amp \neq \amp 0
\end{array}
\end{equation*}
Subsección 2.7.3 Asíntotas de la hipérbola
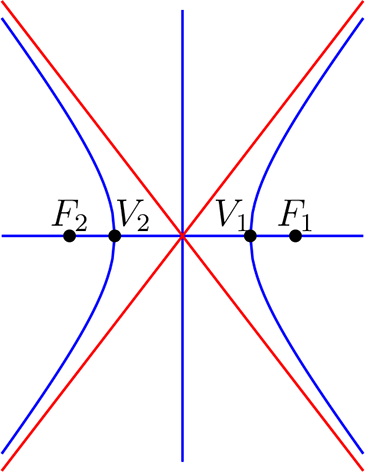
¶Las asíntotas de una hipérbola son rectas que se encuentran tangentes a la hipérbola; es decir, para valores muy grandes la recta y una rama de la hipérbola están muy juntas y que gráficamente se representa de la siguiente forma
Observación: Consideremos la ecuación de la hipérbola donde su eje focal se encuentra en el eje \(X\)
\begin{equation*}
\begin{array}{rcl}
\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} \amp =\amp 1 \ \ \ \ /(a^{2}b^{2})\\
b^{2} x^{2} - a^{2}y^{2} \amp =\amp a^{2} b^{2}
\end{array}
\end{equation*}
Despejemos \(y\)
\begin{equation*}
\begin{array}{rcl}
b^{2} x^{2} - a^{2}y^{2} \amp =\amp a^{2} b^{2} \\
a^{2}y^{2} \amp =\amp b^{2} x^{2} - a^{2}b^{2} \\
y^{2} \amp =\amp \frac{b^{2}x^{2} - a^{2} b^{2}}{a^{2}} \ \ \ \ / \sqrt{} \\
y \amp =\amp \pm \sqrt{\frac{b^{2}x^{2} - a^{2} b^{2}}{a^{2}}} \\
y \amp =\amp \pm \frac{b}{a} \sqrt{(x^{2} - a^{2})} \\
y \amp =\amp \pm \frac{b}{a} \sqrt{x^{2}(1 - \frac{a^{2}}{x^{2}})} \\
y \amp =\amp \pm \frac{b}{a} x \sqrt{(1 - \frac{a^{2}}{x^{2}})}
\end{array}
\end{equation*}
Para valores muy grandes de \(x\) el valor de \(\frac{a^{2}}{x^{2}}\) se va acercando a cero.
Luego
\begin{equation*}
\frac{b}{a} \ x \sqrt{1-\frac{a^{2}}{x^{2}}} \simeq \pm \frac{b}{a} \ x
\end{equation*}
para valores de \(x\) muy grandes
\begin{equation*}
y = \frac{b}{a} \ x, \quad y = - \frac{b}{a} \ x
\end{equation*}
Definición 2.7.9
Sean \(a,b \in \mathbb{R^+}\) y la hipérbola \(\mathcal{H}_{F_{1},F_{2}}\text{.}\)
Si el eje focal es paralelo a eje \(X\text{,}\) su ecuación esta dada por
\begin{equation*}
\frac{(x-h)^{2}}{a^{2}} - \frac{(y-k)^{2}}{b^{2}} = 1
\end{equation*}
entonces la ecuación de las asíntotas de la hipérbola están dadas por
\begin{equation*}
\begin{array}{rcl}
(y-k)=\pm \frac{b}{a} \ (x-h)
\end{array}
\end{equation*}
Si el eje focal es paralelo a eje \(Y\text{,}\) su ecuación esta dada por
\begin{equation*}
\frac{(y-k)^{2}}{a^{2}} - \frac{(x-h)^{2}}{b^{2}} = 1
\end{equation*}
entonces la ecuación de las asíntotas de la hipérbola están dadas por
\begin{equation*}
\begin{array}{rcl}
(y-k)=\pm \frac{a}{b} \ (x-h).
\end{array}
\end{equation*}
Ejemplo 2.7.10
Encuentre el lugar geométrico y toda la información posible de los puntos \(P=(x,y)\) cuya distancia al punto fijo \((1,4)\) sea igual a \(\frac{5}{4}\) de la distancia a la recta \(5x-1=0\text{.}\)
Calculemos la distancia del punto \(P=(x,y)\) al punto \(Q=(1,4)\)
\begin{equation*}
dist(P,Q) = \sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}} = \sqrt{(x-1)^{2}+(y-4)^{2}}
\end{equation*}
Calculemos la distancia del punto \(P\) a la recta \(l:5x-1=0\text{.}\)
\begin{equation*}
\begin{array}{rcl}
dist(l,P) \amp =\amp \frac{\mid Ax +By +C \mid}{\sqrt{A^{2}+B^{2}}} =
\frac{\mid 5x +0y +(-1) \mid}{\sqrt{(5)^{2}+(0)^{2}}} =\frac{\mid
5x -1 \mid}{5}
\end{array}
\end{equation*}
Donde \(dist(P,Q)\) es igual \(\frac{5}{4}\) a \(dist(l,P)\text{.}\)
\begin{equation*}
\begin{array}{rcl}
\sqrt{(x-1)^{2}+(y-4)^{2}} \amp =\amp \frac{5}{4} \frac{\mid 5x -1 \mid}{5} \\
\sqrt{x^{2}-2x+1+y^{2}-8y+16} \amp =\amp \frac{\mid 5x -1 \mid}{4} / \cdot ()^{2} \\
x^{2}-2x+y^{2}-8y+17 \amp =\amp \frac{(5x -1)^{2}}{16}/ \cdot 16 \\
16x^{2}-32x+16y^{2}-128y+272 \amp =\amp 25x^{2}-10x+1\\
9x^{2} +22x -16y^{2}+128y-271 \amp =\amp 0\\
(9x^{2}+22x)+(-16y^{2}+128y) \amp =\amp 271 \\
9\left(x^{2}+ \frac{22}{9}x\right)-16\left(y^{2}-\frac{128}{16}y\right) \amp =\amp 271
\end{array}
\end{equation*}
Ahora completaremos cuadrado
\begin{equation*}
\begin{array}{rcl}
9\left(x^{2}+ 2\frac{11}{9}x + \frac{121}{81}-\frac{121}{81}\right)-16(y^{2}- 2\cdot 4y+16-16) \amp =\amp 271 \\
9\left(x^{2}+2 \frac{11}{9}x + \frac{121}{81}\right)- 9 \cdot \frac{121}{81}-16(y^{2}- 2\cdot 4y+16)-16 \cdot (-16) \amp =\amp 271
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{rcl}
9\left(x+ \frac{11}{9}\right)^{2} -16(y - 4)^{2} \amp =\amp 271+\frac{121}{9}-256
\\
9\left(x+ \frac{11}{9}\right)^{2} - 16(y - 4)^{2} \amp =\amp \frac{256}{9} \\
\frac{(x+ \frac{11}{9})^{2}}{\frac{256}{9\cdot9}} - \frac{(y - 4)^{2}}{\frac{256}{9 \cdot 16}} \amp =\amp 1
\\
\frac{\left(x+ \frac{11}{9} \right)^{2}}{ \left(\frac{16}{9}\right)^{2} } - \frac{\left(y - 4\right)^{2}}{\left(\frac{4}{3}\right)^{2}} \amp =\amp 1
\end{array}
\end{equation*}
De donde podemos obtener que el centro de la hipérbola es \((h,k)=(-\frac{11}{9},4)\text{,}\) además \(a=\frac{16}{9}\) y \(b=\frac{4}{3}\text{,}\) con estos valores obtenemos el valor de \(c\)
\begin{equation*}
\begin{array}{rcl}
c^{2} \amp =\amp a^{2}+b^{2} = \frac{256}{81}+\frac{16}{9} =
\frac{400}{81} =\left(\frac{20}{9}\right)^2
\end{array}
\end{equation*}
entonces \(c=\frac{20}{9}\text{,}\) luego sus focos están dados por:
\begin{equation*}
\begin{array}{rcl}
F_{1}=\left(-\frac{11}{9}-\frac{20}{9},4\right) =\left(-\frac{31}{9},4\right)\amp
\text{y} \amp F_{2}=\left(-\frac{11}{9}+\frac{20}{9},4\right)=(1,4)
\end{array}
\end{equation*}
Los vértices son
\begin{equation*}
\begin{array}{rcl}
V_{1}=\left(-\frac{11}{9}-\frac{16}{9},4\right) =\left(-\frac{27}{9},4\right)\amp \text{y} \amp V_{2}=\left(-\frac{11}{9}+\frac{16}{9},4\right)=\left(\frac{5}{9},4\right)
\end{array}
\end{equation*}
Las asíntotas están dadas por
\begin{equation*}
\begin{array}{rcl}
(y-k) \amp =\amp \pm \frac{b}{a}(x-h) \\
(y-4) \amp =\amp \pm \frac{\frac{16}{12}}{\frac{16}{9}}(x+\frac{11}{9}) \\
(y-4)= \frac{3}{4} (x+\frac{11}{9}) \amp \text{y} \amp (y-4)= -\frac{3}{4}
(x+\frac{11}{9}).
\end{array}
\end{equation*}
Subsección 2.7.4 Ejercicios Propuestos
¶
-
Graficar y encontrar todos los elementos que componen a la cónica de ecuación
- \(9y^{2}=16x^{2}-36y-96x+684\)
- \(9x^{2}-25y^{2}-18x-50y=191\)
-
Considere la recta \(l_{m}\) de ecuación \(y=mx+1\text{.}\) Determine todos los valores de \(m \in \mathbb{R}\) tales que las recta \(l_{m}\) interseca a la hipérbola \(\frac{y^{2}}{4} - \frac{x^{2}}{2}=1\text{.}\)
[Resp. \(m \in \ \Big] - \sqrt{\frac{3}{2}}, \sqrt{\frac{3}{2}}
\Big[ \ y \ m \neq \pm \sqrt{2}\) ]
-
Hallar e identificar la ecuación del lugar geométrico de un punto que se mueve de tal manera que su distancia del punto \((6,0)\) es siempre igual al doble de su distancia de la recta \(2x-3=0\)
[Resp. \(3x^{2}-y^{2}=27\) ]
-
Hallar la ecuación de la hipérbola que pasa por el punto \((4,6)\text{,}\) tiene el eje focal paralelo al eje \(X\text{,}\) y sus asíntotas son las rectas \(2x+y-3=0\) y \(2x-y-1=0\text{.}\)
[Resp. \(4x^{2}-y^{2}-8x+2y-8=0\) ]
-
Hallar e identificar la ecuación del lugar geométrico de un punto que se mueve de tal manera que su distancia del punto \((3,2)\) es siempre igual al doble de su distancia de la recta \(y+1=0\text{.}\)
[Resp. \(x^{2}-8y^{2}-6x-22y+4=0\) ]
-
Hallar e identificar la ecuación del lugar geométrico de un punto que se mueve de tal manera que su distancia del punto \((2,-1)\) es siempre igual al doble de su distancia de la recta \(x+2=0\text{.}\)
[Resp. \(3x^{2}-y^{2}+20x-2y+11=0\) ]
-
Hallar los valores de \(m\) para los cuales las rectas de la familia \(y=mx-1\) son tangentes a la hipérbola \(4x^{2}-9y^{2}=36\)
[Resp. \(m = \pm \frac{\sqrt{5}}{3}\) ]
Demostrar que la elipse \(2x^{2}+y^{2}=10\) y la hipérbola \(4y^{2}-x^{2}=4\) se intersecan.