Sección 3.4 Tipos de Funciones
¶Sean \(A\) y \(B\) subconjuntos de \(\mathbb{R}\) y \(f :A\longrightarrow B\) una función real.
Una clasificación de las funciones reales es la siguiente:
Funciones LinealesSon funciones de la forma \(\begin{array}[t]{ccccl} f: \amp \mathbb{R} \amp \longrightarrow \amp \mathbb{R},\\ \amp x \amp \longmapsto \amp mx+b \end{array}\) con \(m,b\in\mathbb{R}\text{.}\)
La gráfica de las funciones lineales, corresponde a una recta de pendiente \(m.\)
Si \(m \gt 0\) y \(b\neq 0\) su gráfica tiene la siguiente forma:
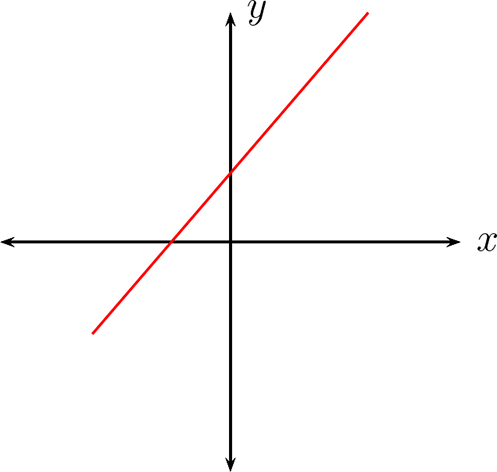
Si \(m \lt 0\) y \(b\neq 0\text{,}\) se gráfica es del siguiente tipo:
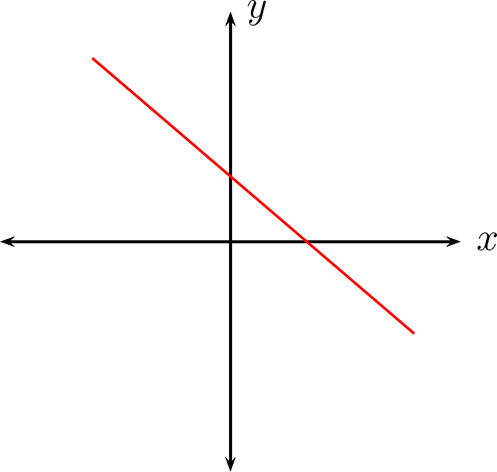
Si \(m=1\) y \(b=0\text{,}\) entonces llamaremos a esta función Identidad y se define como:
Su gráfica :
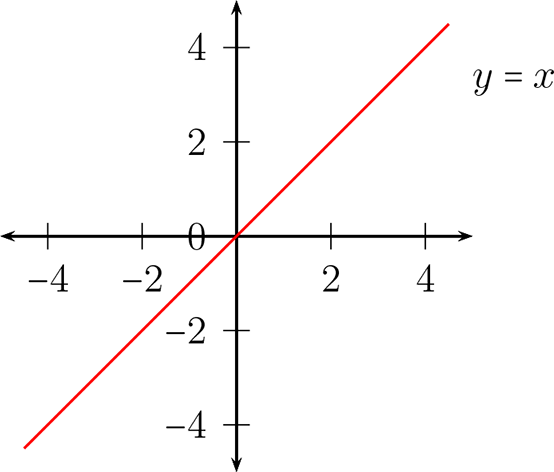
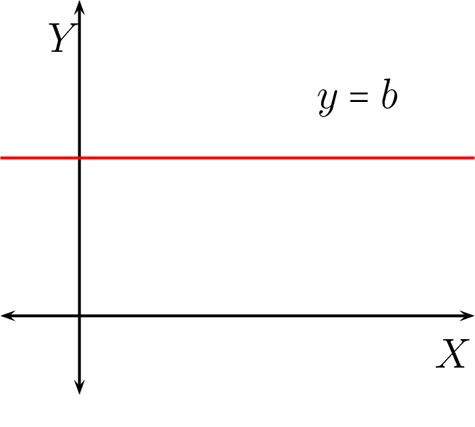
Si \(m=0\) y \(b\neq 0\text{,}\)entonces la función se llama función constante \(b\) y se denota por
Gráficamente de pendiente cero:
Son funciones del tipo \(\begin{array}[t]{cccl} f: \amp \mathbb{R} \amp \longrightarrow \amp \mathbb{R},\\ \amp x \amp \longmapsto \amp ax^2+bx+c \end{array}\) con \(a,b,c\in\mathbb{R}\) y \(a\not =0\text{.}\)
La gráfica de la función cuadrática \(y=ax^2+bx+c\text{,}\) corresponde a una parábola.
Para conocer la gráfica de una parábola es útil calcular su vértice
donde \(\triangle=b^2-4ac\text{,}\) es el discriminante de la ecuación, de segundo grado o polinomio de segundo grado y las intersecciones con el eje \(X\text{,}\) cuya existencia depende del valor del discriminante si es negativo o no es. El nombre de \(\Delta\) se debe a que discrimina si la función cuadrática tiene intercepto en eje \(X \) o no hay, de otro modo, si la ecuación tiene o no tiene solución en el conjunto de los números reales.
Cuando \(a \gt 0\) su gráfica corresponde a una parábola que se abre hacia arriba.
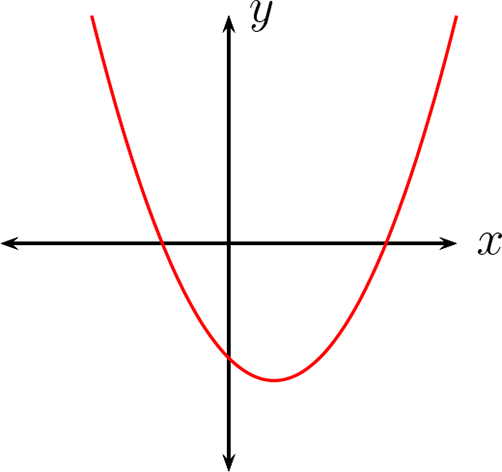
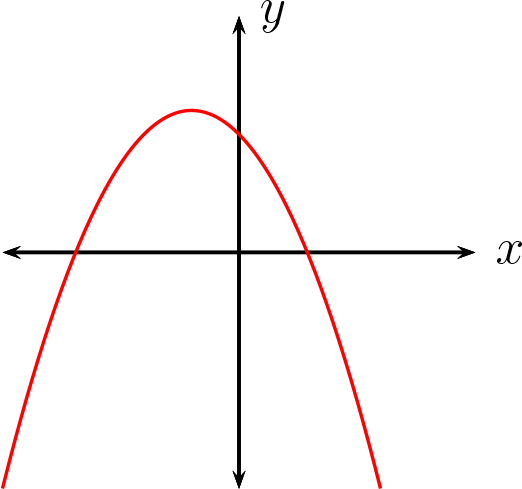
Cuando \(a \lt 0\) su gráfica corresponde a una parábola que se abre hacia abajo.
Esta esta dada por:
La gráfica de la función es la siguiente:
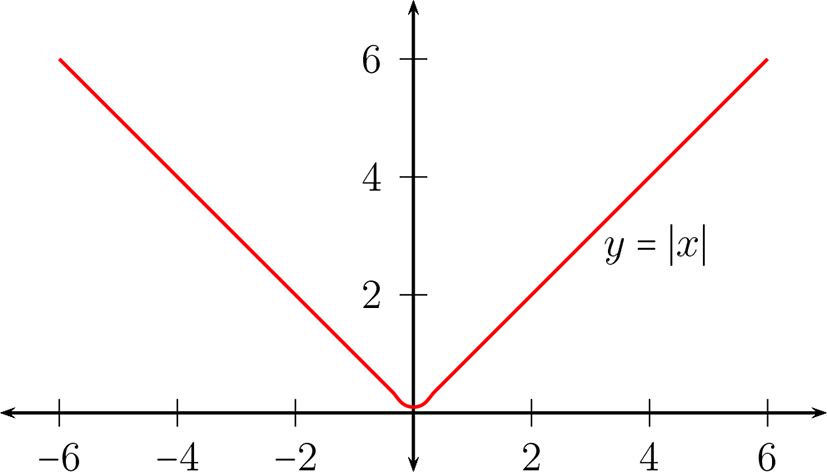
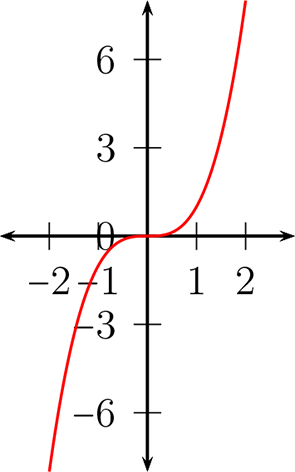
Esta función esta dada por:
La gráfica de la función es la siguiente:
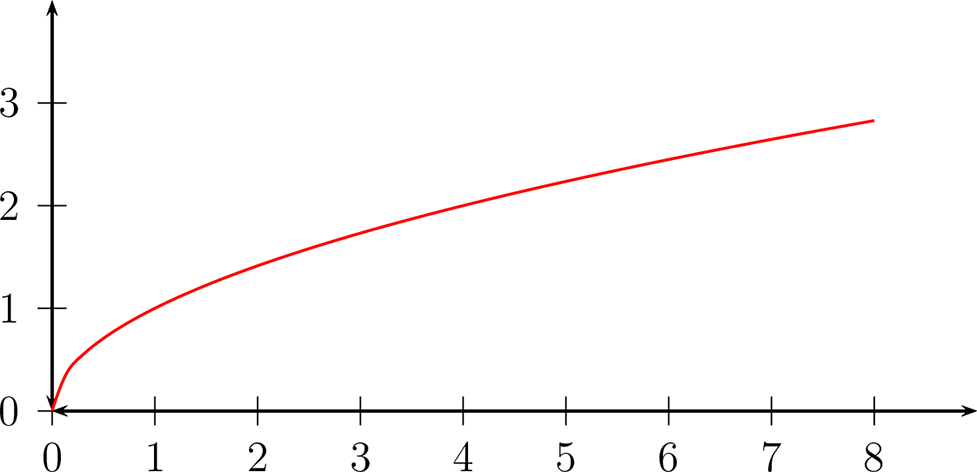
Esta función esta dada por:
Gráficamente:
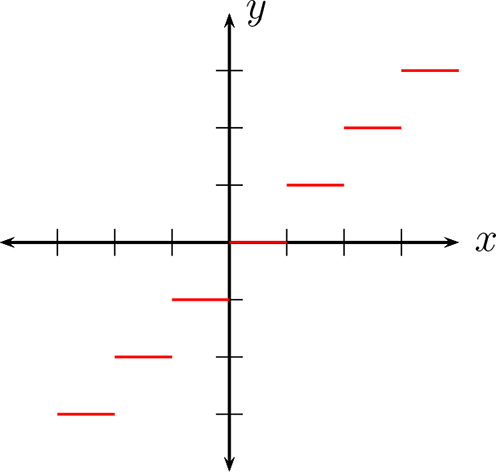
Dado un número real \(x\text{,}\) se puede descomponer en una suma separando su parte entera
luego la parte decimal se define
o bien
donde \([x]\) es un número entero y \(d(x)\) un número decimal, \(0\leq d(x) \lt 1.\)
Luego la función parte entera se define como:
Su gráfica:
Ejercicios Propuestos Sea \(f:A\subseteq \mathbb{R}\longrightarrow \mathbb{R}.\) Determine el conjunto \(A\) igual al dominio máximo de \(f\) y el recorrido para ese dominio.
- \(f(x)=\frac{x-2}{x-3} \)
- \(f(x)=\sqrt{1-x^2} \)
- \(f(x)=x^2+x-1\)
- \(f(x)=\frac{x+1}{x^2+x+1} \)
- \(f(x)=\sqrt{\frac{x}{|x|-1}}\)
- \(f(x)=\frac{\sqrt{1-|x|}}{{1+x^2}}\)
