Sección 2.3 Ecuación de la Recta
¶La geometría euclidiana nos enseña que dados dos puntos distintos, existe una única recta que contiene a los puntos.
De este modo se tiene que una recta es el conjunto todos los puntos colineales a dos puntos dados.
Sean \(P_{1},P_{2} \in \mathbb{R}^{2}\text{,}\) luego la recta que pasa por los \(P_{1}=(x_{1},y_{1}) , P_{2}=(x_{2}, y_{2})\) es
Llamaremos línea recta o simplemente recta a la figura geométrica que resulta al graficar los puntos de este conjunto en el plano cartesiano \(\mathbb{R}^{2}\text{.}\)
Observación: Para una mayor comodidad de escritura, al conjunto que forma una recta
lo denotaremos por su ecuación, es decir,
Hallar las ecuaciones de la recta \(l\) que pasan por los puntos \((5,-9) \ y \ (1,3)\text{.}\)
Sabemos que \((5,-9) \ y \ (1,6) \in l\text{,}\) donde \((5,-9) = (x_{1} , y_{1})\) y \((1,6) = (x_{2} , y_{2})\) tenemos
Subsección 2.3.1 Ecuaciones de la Rectas
¶Definición 2.3.2
Sean \(P_{1}=(x_{1},y_{1}) , P_{2}=(x_{2}, y_{2}) \in l\) puntos distintos, se define la pendiente de la recta \(l\) en los siguientes casos
-
Si \(x_{2}=x_{1}\text{,}\) diremos que la pendiente es infinita, y escribiremos \(m = \infty\) entonces la recta \(l\) es
\begin{equation*} l=\{ (x,y) \in \mathbb{R}^{2} \ : \ \ x = x_1 \} \ \ \ \text{o} \ \ \ l:x = x_1 \end{equation*} -
Si \(x_{2} \neq x_{1}\text{,}\) se define la pendiente
\begin{equation*} m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} \end{equation*}entonces la recta \(l\) es
\begin{equation*} l=\{ (x,y) \in \mathbb{R}^{2} \ : \ \ y =mx+b \} \ \ \ \text{o} \ \ \ l:y = mx+b \end{equation*}con
\begin{equation*} b= \frac{x_2y_1-x_1y_2}{x_{2}-x_{1}} \end{equation*}
Observación: Un caso particular es cuando la pendiente de \(l\) toma el valor \(0\text{,}\) es decir \(m = 0\) entonces la ecuación de la recta \(l\) es
Dependiendo del valor de la pendiente se puede se pueden distinguir dos tipos de inclinación al graficar una recta, es decir, cuando la pendiente es positiva tenemos que es creciente y cuando es negativa es decreciente
este comportamiento lo observaremos mediante dos ejemplos, la recta graficada de color rojo \(y=3x+5\) es creciente y la recta graficada de color azul \(y=-2x+4\) es decreciente
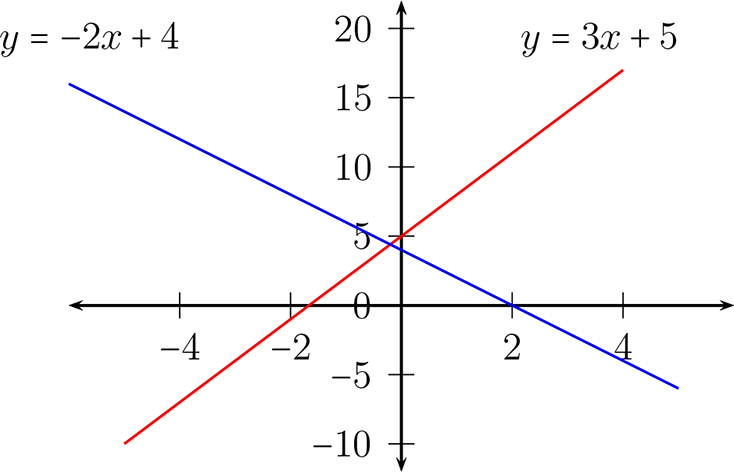
En los otros casos, la gráfica de las rectas cuando \(m = \infty \) son gráficas verticales del forma que tiene la de color rojo y cuando \(m = 0\) son gráficas horizontales corresponde a la forma de color azul, dada en la siguiente figura

Ejemplo 2.3.3
Sean \(A=(6,11)\) y \(B=(13,4) \in \mathbb{R}^{2}\) dos puntos que pertenece a la recta \(l\text{.}\) Calcule la pendiente de la recta \(l\text{.}\)
Sean \(A=(x_{1},y_{1})=(6,11)\) y \(B=(x_{2},y_{2})=(13,4)\text{,}\) reemplazando en la formula de la pendiente tenemos:
Por lo tanto, la pendiente de la recta \(l\) es \(-1\text{.}\)
Ejemplo 2.3.4
Calcule las pendientes de las rectas que pasan por el punto medio del segmento \(\overline{AB}\) con \(A=(5,7)\text{,}\) \(B = (12,3)\) y que pasan por un punto que es colineales a los puntos de \(C=(16,14)\) y \(D =(8,10)\text{.}\)
Sea \(A=(5,7)\) y \(B=(12,3)\text{,}\) luego el punto medio de \(\overline{AB}\) esta dado por:
Consideremos los puntos colineales a \(C=(16,14)\) y \(D=(8,10)\) que denotaremos como \(P=(a,b)\text{.}\) Reemplazando tenemos que
Reemplazando \(a=2b-12\) en el punto \(P=(a,b)\text{,}\) tenemos que \(P = (2b-12 , b)\)
Luego si \(Q = \left( \frac{17}{2} , 5 \right) = (x_{1} , y_{1}) \) y \(P = (2b-12 , b) = (x_{2} , y_{2}) \) su pendiente es
Por lo tanto todas las rectas que pasan por el punto medio del segmento \(\overline{AB}\) y por los posibles puntos colineales de \(C \ y \ D\) tienen como pendiente
El problema esta representado por la siguiente figura,
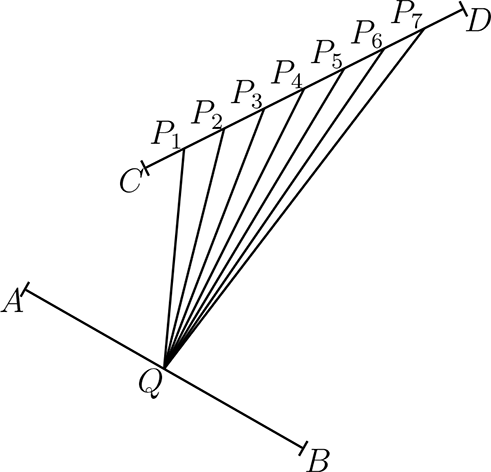
Donde \(Q = (\frac{17}{2},5)\) es el punto medio del segmento \(\overline{AB}\) y \(P_{1},P_{2},P_{3},P_{4},P_{5},P_{6}, P_{7},P_{8},P_{9} \) son algunos puntos colineales a \(C \text{ y } D\)
Finalmente sus ecuaciones están dadas por:
donde \(P_{b}=(2b-12,b)\) punto colineal de \(\overline{CD}\text{,}\) con \(b\in \mathbb{R}\text{.}\)
A continuación daremos algunas indicaciones para determinar la ecuación de la recta, dependiendo de los datos proporcionados por el problema.
Primer Caso: Se conoce un punto de la recta y su pendiente.
La ecuación de la recta \(l\) queda totalmente determinada con un punto \(P_1=(x_1,y_1)\) y su pendiente \(m\text{.}\)
a) Si la pendiente \(m=\infty \) entonces la recta es:
b) Si la pendiente \(m \in \mathbb{R}\text{,}\) luego sea \(P=(x,y) \in l\text{,}\) otro punto de la recta, así tenemos que
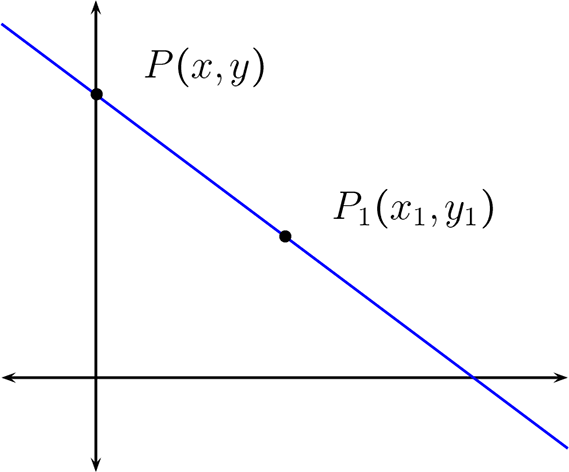
Proposición 2.3.5
Sean \(P_{1}=(x_{1},y_{1}) \in \mathbb{R}^{2}\) un punto de la recta y \(m \in \mathbb{R}\) donde \(m\) representa la pendiente de la recta \(l\) entonces la ecuación de la recta está dada por:
Ejemplo 2.3.6
Encuentre la ecuación de la recta que pasa por el punto \(A=(11,3)\) y su pendiente es \(m = 13\text{.}\)
Como la recta pasa por el punto \(A=(x_{1},y_{1}) =(11,3)\) y su pendiente es \(m=13\text{,}\) reemplazando en la ecuación de la propiedad anterior, se tiene
Por lo tanto la ecuación de la recta esta dada por
Segundo Caso: Se conocen dos puntos de la recta.
Sabemos que la ecuación de la recta \(l\) queda totalmente determinada por dos puntos.
Sean \(P_{1}=(x_{1},y_{1}),P_{2}=(x_{2},y_{2}) \in \mathbb{R}^{2}\text{,}\) puntos en la recta
a) Si \(x_{1} \neq x_{2}\text{,}\) reemplazando en la definición de pendiente obtenemos
para luego reemplazar en el caso anterior, y obtener
Si \(x_{1} = x_{2}\) entonces la ecuación es
Proposición 2.3.7
Sean \(P_{2}=(x_{2},y_{2}) , P_{1}=(x_{1},y_{1}) \in \mathbb{R}^{2}\) con \(x_{1} \neq x_{2}\text{,}\) entonces la ecuación de la recta que pasa por dos puntos dados es:
Ejemplo 2.3.8
Encuentre la ecuación de la recta que pasa por el punto \((1,9)\) y por el punto \((5,7)\text{.}\)
Ya que la recta pasa por los puntos \(A=(x_{1},y_{1})=(1,9)\) y \(B=(x_{2},y_{2})=(5,7)\text{.}\)
Reemplazando \(A\) y \(B\) en la definición de pendiente tenemos
Y la pendiente en ecuación obtenida anteriormente tenemos lo siguiente
Observación: Tenga presente que, la ecuación de la recta no varía, al considerar en diferente orden los puntos.
Ejemplo 2.3.9
La recta \(l\) interseca al eje \(Y\) en el punto \((0,6)\) y pasa por el punto \((5,8)\text{.}\) Encuentre la ecuación de la recta \(l\text{.}\)
Consideremos los puntos \(A=(x_{1},y_{1})=(0,6)\) y el punto \(B=(x_{2},y_{2})=(5,8)\text{,}\) luego calculemos su pendiente.
Luego reemplazando en la ecuación tenemos
Despejando \(y\) obtenemos la ecuación pedida.
Observación: La ecuación de la recta se puede escribir de varias maneras y de acuerdo a esta escritura es que recibe distintos nombres
Definición 2.3.10
Sean \(A,B,C,a,b,m \in \mathbb{R}\) y \(l\) una recta, entonces
-
Se dice que la recta
\begin{equation*} \label{a_8} l: Ax + By + C = 0. \end{equation*}esta definida por la ecuación general o que \(Ax + By + C = 0\) es la ecuación general de la recta.
-
Se dice que la recta
\begin{equation*} l: \frac{x}{a}+ \frac{y}{b} = 1. \end{equation*}esta definida por la ecuación simétrica o que \(\frac{x}{a}+ \frac{y}{b} = 1 \) es la ecuación simétrica de la recta.
-
Se dice que la recta esta definida por la ecuación pendiente-ordenada o reducida cuando la ecuación tiene la siguiente forma
\begin{equation*} l:y = mx + b. \end{equation*}
Ejemplo 2.3.11
Considere la ecuación de la recta
Encuentre la ecuación general, ecuación simétrica y la pendiente-ordenada.
Sea \(y-7 = \frac{10}{3}(x-4)\)
-
Consideremos la ecuación de la recta
\begin{equation*} \begin{array}{rcl} y-7 \amp =\amp \frac{10}{3} \ (x-4) \\ y-7 \amp =\amp \frac{10}{3} \ x - \frac{40}{3} \ \ / \cdot 3 \\ 3y - 21 \amp =\amp 10x - 40 \\ 10x -3y - 19 \amp =\amp 0 \end{array} \end{equation*}Por lo tanto la ecuación general de la recta es:
\begin{equation*} 10x -3y - 19 = 0 \end{equation*} -
Tomemos la ecuación general \(10x -3y - 19 = 0 \)
\begin{equation*} \begin{array}{rcl} 10x -3y - 19 \amp =\amp 0 \\ 10x -3y \amp =\amp 19 \ \ / \cdot \frac{1}{19} \\ \frac{10}{19}x - \frac{3}{19}y \amp =\amp 1 \\ \frac{x}{\frac{19}{10}}- \frac{y}{\frac{19}{3}} \amp =\amp 1 \end{array} \end{equation*}Por lo tanto la ecuación simétrica de la recta es:
\begin{equation*} \frac{x}{\frac{19}{10}} + \frac{y}{-\frac{19}{3}} = 1 \end{equation*} -
Consideremos la ecuación general \(10x -3y - 19 = 0\)
\begin{equation*} \begin{array}{rcl} 10x -3y - 19 \amp =\amp 0 \\ 3y \amp =\amp 10x -19 \ \ / \cdot \frac{1}{3} \\ y \amp =\amp \frac{10}{3} \ x - \frac{19}{3} \end{array} \end{equation*}Por lo tanto la ecuación pendiente-punto es:
\begin{equation*} y = \frac{10}{3} \ x - \frac{19}{3} \end{equation*}
Ejemplo 2.3.12
Si \(l_1\) es una recta que pasa por los puntos \((7,11) ,(3,4) \) y \(l_2\) es una recta de pendiente \(13\) y pasa por \((8,5)\text{.}\)
Hallar la intersección de las rectas \(l_{1}\) y \(l_{2}\text{.}\)
Sabemos que \((7,11), (3,4) \in l_{1}\) , luego tenemos que
Así tenemos la ecuación de la recta \(l_{1} : 4y - 7x + 5 = 0\text{.}\)
Para \(l_2\) tenemos que pasa por \((8,5) = (x_{1} , y_{1}) \in l_{2}\) y su pendiente es \(13\text{.}\) luego la ecuación es
Sea \(P\) es el punto de intersección de \(l_{1}\) y \(l_{2}\text{,}\) es decir, \(l_{1} \cap l_{2} = \{P\}\text{,}\) luego satisface las ecuaciones anteriores, por lo tanto tenemos que
despejando \(y\) de la segunda ecuación obtenemos
y reemplazando en la primera tenemos
Reemplazamos \(x=\frac{391}{45}\) en \(y = 13x - 99\) entonces
Luego el punto intersección es \(P=(\frac{391}{45},\frac{628}{45})\text{.}\)
Subsección 2.3.2 Rectas Paralelas o Perpendiculares
¶El esta sección se tratara el temas de rectas paralelas o perpendiculares y las condiciones que deben satisfacer los coeficiente que define las rectas para que ellas cumplas una de estas condiciones.
La noción de cuando dos rectas son paralelas cuando no tiene punto en común o son iguales, y la de recta son perpendiculares cuando el punto intercepto de ella forme cuatro regiones iguales
Gráficamente tenemos que si \(l_{1} , l_{2}\) son rectas de la forma
entonces representamos gráficamente el paralelismo y perpendicularidad de la siguiente forma

Subsección 2.3.3 Rectas Paralelas
¶Definición 2.3.13
Diremos que dos rectas \(l_{1},l_{2}\) son paralelas o \(l_{1} // l_{2}\) si estas no se intersecan en ningún punto o bien son iguales.
Proposición 2.3.14
Las rectas \(l_{1}\) y \(l_{2}\) son paralelas si y sólo si
es decir, \(l_{1} // l_{2}\) si y sólo si las pendientes son iguales.
Dadas dos rectas distintas, los sistemas de ecuaciones
no tiene solución si y solo si \(m_1 = m_2\) o bien \(A_{1}B_{2} = A_{2}B_{1}\)
Ejemplo 2.3.15
Sean las rectas \(l_{1}: 3y + 4x -15 = 0\) y \(l_{2}: 9y + 12x + 21 = 0\text{,}\) verifique si \(l_{1} // l_{2}\text{.}\)
Como \(l_{1}: 3y + 4x -15 = 0\) y \(l_{2}: 9y + 12x + 21 = 0\) tenemos
Luego
Por lo tanto, las rectas \(l_{1}\) y \(l_{2}\) son rectas paralelas, es decir, \(l_{1} // l_{2}\)
Subsección 2.3.4 Rectas Perpendiculares
¶Definición 2.3.16
Diremos que dos rectas son perpendiculares si y sólo si se intersecan en un punto formando un ángulo de \(90^{\circ}\text{.}\)
Proposición 2.3.17
Las rectas \(l_{1}\) y \(l_{2}\) son perpendiculares si y sólo si
es decir, \(l_{1} \perp l_{2}\) si y sólo si la multiplicación de sus pendientes es igual a \(-1\) o una es horizontal y la otra vertical.
Dadas las rectas \(l_1: y-a = m_1(x-b) \) y \(l_2: y-a = m_2(x-b) \) cuya intercepto es el punto \(R(a,b)\text{,}\) otros punto de cada recta son \(P(a+1,b+m_1)\in l_1\) y \(Q(a+1,b+m_2)\in l_2\text{,}\) luego deben formar un triángulo rectángulo, como en la figura.
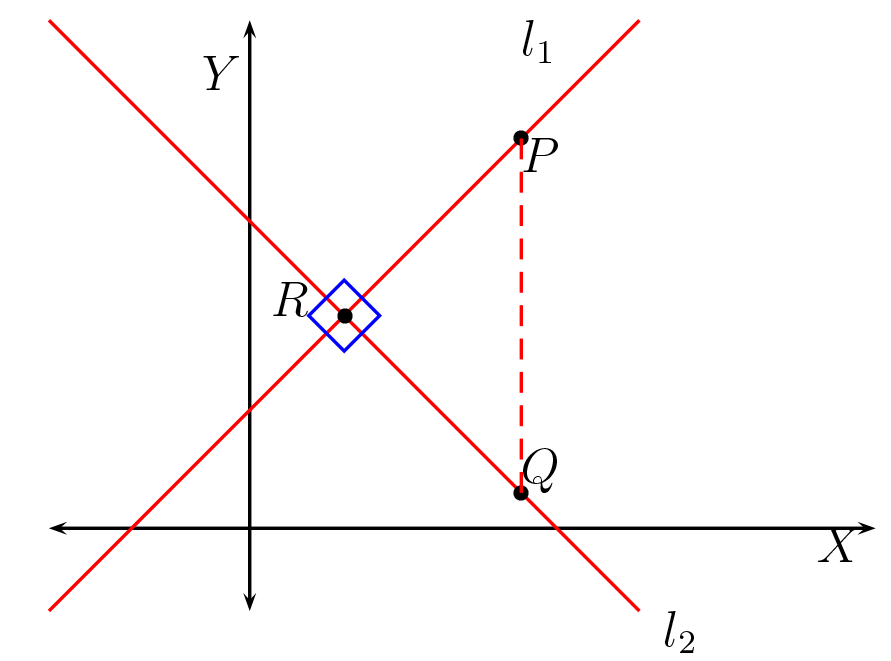
Usando pitágoras tenemos que \((dist(P,R))^2 + (dist(R,Q))^2=(dist(P,Q))^2 \text{,}\) reemplazando los puntos se tiene
Y ahora reemplazando en la igualdad pitagórica obtenemos
al simplificando, se obtiene que \(2=-2m_1m_2\text{,}\) es decir, \(m_1m_2=-1\)
Ejemplo 2.3.18
Sean las rectas \(l_{1}: 2y - 7x - 24 = 0\) y \(l_{2}: 28y + 8 x + 13 = 0\text{,}\) verifique si \(l_{1} \perp l_{2}\text{.}\)
Como \(l_{1}: 2y - 7x - 24 = 0\) y \(l_{2}: 28y + 8 x + 13 = 0\) tenemos
Por otro lado
Luego
donde
Por lo tanto, se tiene que las rectas \(l_{1}\) y \(l_{2}\) son rectas perpendiculares, es decir, \(l_{1} \perp l_{2}\text{.}\)
Definición 2.3.19
Diremos que dos rectas son coincidentes si y sólo si las rectas son iguales.
Proposición 2.3.20
Dadas \(l_1, l_2\) dos rectas entonces
-
Las rectas \(l_{1}: y= m_1x+b_1 \) y \(l_{2} : y=m_2x + b_2\) son coincidente si y sólo si
\begin{equation*} m_1=m_2 \quad \text{ y }\quad b_1 = b_2 \end{equation*} -
Las rectas \(l_{1}: A_{1}x + B_{1}y + C_{1}\) y \(l_{2} : A_{2}x + B_{2}y + C_{2}\) son coincidente si y sólo si
\begin{equation*} C_{1}B_{2} = C_{2}B_{1} \quad \text{ y }\quad A_{1}B_{2} = A_{2}B_{1} \quad \text{ y }\quad A_{1}C_{2} = A_{2}C_{1} \end{equation*}
Proposición 2.3.21
Dada la recta
y el punto \(P=(x_1,y_1)\) entonces tenemos
-
La ecuación de la recta \(l_1\) perpendicular a \(l\) que pasa por \(P\) es
\begin{equation*} l_1:\ \ B(x-x_1)-A(y-y_1)=0 \end{equation*} -
La ecuación de la recta \(l_2\) paralela a \(l\) que pasa por \(P\) es
\begin{equation*} l_2:\ \ A(x-x_1)+B(y-y_1)=0 \end{equation*}
Ejemplo 2.3.22
Sean \(A=(2,5),B=(7,3)\) y \(l_{1}, l_{2} \subseteq \mathbb{R}^{2}\) rectas tales que \(A,B \in l_{2}\) y
Encuentre el valor de \(k \in \mathbb{R}\) en cada caso de modo que:
- \(l_{1} \perp l_{2}\text{.}\)
- \(l_{1} // \ l_{2}\text{.}\)
Calculemos la pendiente de \(l_{2}\) con \(A=(x_{1},y_{1})=(2,5)\) y \(B=(x_{2},y_{2})=(7,3)\) entonces
Entonces tomando el punto \(A=(2,5)\) y la pendiente \(m_{2}= \frac{1}{2}\text{,}\) la ecuación de la recta \(l_{2}\) esta dada por:
Luego la pendiente de \(l_{1}\) la podemos obtener de la escritura de la recta:
Observación: El valor de \(k\) no puede ser igual a \(-3\) en cuyo caso la pendiente es infinito y no serían paralela ni perpendiculares.
Por lo tanto la pendiente de \(l_{1}\) es
-
Para que \(l_{1} \perp l_{2}\) necesitamos que \(m_{1} \cdot m_{2} = -1\) luego tenemos:
\begin{equation*} \begin{array}{rcl} \frac{1}{2} \cdot \frac{-k}{k+3} \amp =\amp -1 \\ -k \amp =\amp -2(k+3) \ \ / \cdot (-1) \\ k \amp =\amp 2k +6 \\ k \amp =\amp -6. \end{array} \end{equation*}Reemplazando \(k\) en la ecuación obtenemos
\begin{equation*} l_{1}: y=-\frac{6}{3}x+ \frac{5}{3} \ \ \text{y} \ \ l_{2}: y = \frac{1}{2}x+4 \end{equation*}son perpendiculares.
-
Para que \(l_{1} // \ l_{2}\) necesitamos que \(m_{1} = m_{2}\)
\begin{equation*} \begin{array}{rcl} \frac{-k}{k+3} \amp =\amp \frac{1}{2} \\ -2k \amp =\amp k+3 \\ -3k \amp =\amp 3 \\ k \amp =\amp -1 \end{array} \end{equation*}Reemplazando el valor de \(k\) en la ecuación de la recta \(l_{1}\) tenemos que:
\begin{equation*} l_{1}: y = \frac{1}{2}x-\frac{5}{2} \ \ \text{y} \ \ l_{2}: y = \frac{1}{2}x+4 \end{equation*}son paralelas.
Subsección 2.3.5 Distancia de un Punto a una Recta
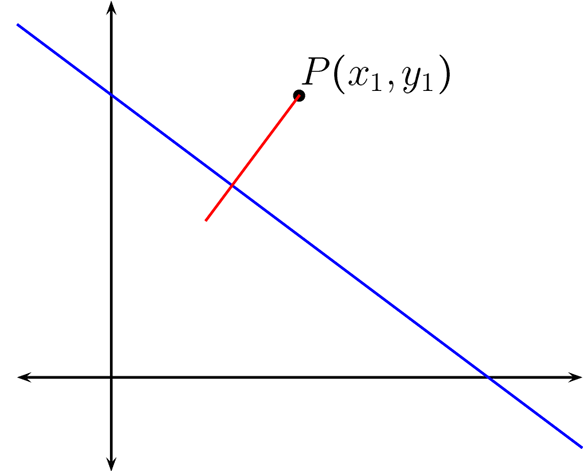
¶La distancia de un punto a una recta, es la distancia más corta del punto a cualquier de los puntos que pertenezcan a la recta. Note que este punto corresponde a un punto cuya recta es perpendicular a la recta original y pasa por el punto dado, ya que los otros puntos formarían los vértices de un triángulo rectángulo cuya hipotenusa tiene una longitud mayor que el lado correspondiente.
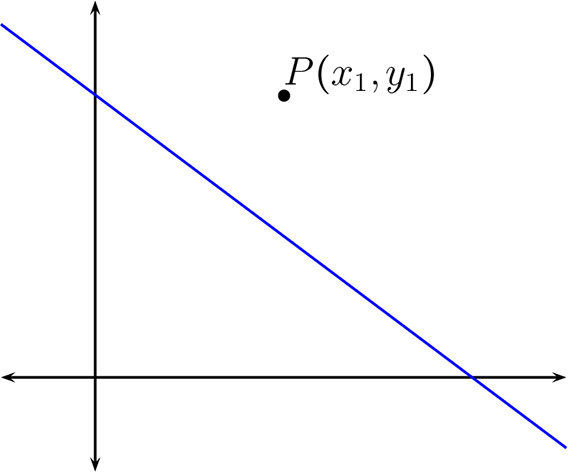
Proposición 2.3.23
Sea \(P = (x_{1}, y_{1})\in \mathbb{R}^{2}\) y la recta cuya ecuación es
entonces la distancia de un punto \(P\) a la recta \(l\) esta dada por:
o por
Demostración
Sea \(l\) una recta de ecuación \(Ax + By =C\) y \(P = (x_{1},y_{1}) \in \mathbb{R}^{2}\text{.}\)
Sean \(l_{1}\) perpendicular a \(l\) y \(P \in l_{1}\text{,}\) luego tenemos que
Calculemos \(Q=(x,y)\) el punto de intersección de \(l\) con \(l_{1}\)
Multiplicando la primera ecuación por \(A\text{,}\) la segunda por \(B\) y sumamos obtenemos
Análogamente obtenemos
Luego calculemos \(dist (P,Q)\) donde \(P = (x_{1} , y_{1})\) y \(Q = (x,y)\)
Calculemos primeros \((x-x_1)^2\)
Calculemos ahora \((y-y_1)^2\)
Reemplazando obtenemos
De lo cual
Ejemplo 2.3.24
Dada la recta \(2x+3y+4=0\) y el punto \(P=(1,3)\text{.}\)
Determine la distancia entre \(P\) y \(l\text{.}\)
Dada la recta \(-4x+3y+4=0\) y el punto \(P=(1,3)\)
Ejemplo 2.3.25
Dado los puntos \(A=(-1,4)\text{,}\) \(B=(1,2)\) y \(C=(3,-2)\text{.}\)
Determine el área del triángulo \(ABC\) (con vértices en los puntos \(A,B,C\)).
Ya que \(A(-1,4)\text{,}\) \(B(1,2)\) y \(C(3,-2)\text{.}\)
La recta que pasa por \(A, B\) es
es decir \(l_{AB}: y+x=3\text{.}\)
Luego el área del triángulo es
Luego el área del triángulo \(ABC\) es \(2\text{.}\)
Subsección 2.3.6 Ejercicios Propuestos
¶Demuestre que los puntos \(A=(-3,1)\) , \(B=(5,3)\text{,}\) \(C=(3,9)\) y \(D=(-5,7)\) son los vértices de un paralelogramo.
-
Dados los puntos \(A=(-4,1)\) y \(B=(1,-1)\text{,}\) determine todos los puntos \(C\) sobre la recta de ecuación \(y=x+4\) para los cuales el triángulo de vértices \(ABC\) tenga área igual a \(1\text{.}\)
\([ Resp.\ \ C=(3,7) \ o \ C=(-3,1) ]\)
-
Considere los puntos del plano \(A=(1,2)\) y \(B=(3,5)\) y sea \(\overline{AB}\) el segmento que los une. Determine la ecuación de la recta que pasa por el punto medio de \(\overline{AB}\) y es perpendicular a la recta que une \(A\) con \(B\text{.}\)
\([ Resp.\ \ 4x+6y-29 =0 ]\) -
Encuentre la ecuación de la altura del triángulo \(ABC\) donde \(\overline{AB}\) representa la base y \(A=(-1,4)\) , \(B=(1,2)\) y \(C=(3,-2)\text{.}\)
\([ Resp.\ \ y-x-3 = 0 ]\) -
Sea la ecuación de la recta \(L: (k+1)y - kx - 3 = 0\text{,}\) encuentre el valor de \(k \in \mathbb{R}\) para los siguientes casos:
\(L\) pasa por el punto \((-1,2)\text{.}\) \([ Resp.\ \ k= \frac{1}{3}]\)
\(L\) sea horizontal.\([ Resp.\ \ k = 0 ]\)
\(L\) sea paralela a la recta de ecuación \(3y+x-2 = 0\text{.}\) \([ Resp.\ \ k= \frac{-1}{4} ]\)
-
\(L\) sea perpendicular a la recta de ecuación \(2x-3y+1 = 0\text{.}\)
\([ Resp.\ \ k= \frac{-3}{5} ]\) -
\(L\) sea vertical.
\([ Resp.\ \ k= -1 ]\)
-
Sean \(l_{1}\) y \(l_{2}\) las rectas cuyas ecuaciones son \(x+2y=3\) y \(-2x+y=4\text{,}\) respectivamente. Determine la ecuación de la recta \(l\) que pasa por el punto de intersección entre \(l_{1}\) y \(l_{2}\) y que es perpendicular a la recta \(l_{3}: 3x-y-1 = 0\text{.}\)
\([ Resp.\ \ l:x+3y-5 = 0 ]\) -
Determinar el área del triángulo de vértices \((-2,-1),(1,4)\) y \((3,-3)\text{.}\)
\([ Resp.\ \ \frac{31}{2} ]\) -
Determinar la ecuación de la recta que pasa por \(P=(-2,3)\) y es perpendicular a la recta \(l:3x-2y+5=0\text{.}\)
\([ Resp.\ \ 2x+3y-5=0 ]\) -
Dadas las rectas \(l_{1}:2x-3y-2=0\text{,}\) \(l_{2}:3x-2y+1=0\) y \(l_{3}: x+4y-3=0\text{.}\) Determinar la distancia del punto de intersección de \(l_{1}\) con \(l_{2}\) a la recta \(l_{3}\text{.}\)
\([ Resp. \ \approx 2.6 ]\) -
Determine la recta \(l\) que esta a una distancia \(\sqrt{2}\) del punto \(P=(1,-2)\) e interseca perpendicularmente a la \(l_1:3x-y+1=0\text{.}\)
\([ Resp.\ \ x+3y+(5-2\sqrt{5})=0 \ o \ x+3y+(5+2 \sqrt{5})=0 ]\) -
Hallar la ecuación de la recta cuya pendiente es \(-4\) y que pasa por el punto de intersección de las rectas \(2x+y-8 = 0\) y \(3x-2y+9=0\text{.}\)
\([ Resp.\ \ 4x+y-10 = 0 ]\) -
Sean \(A=(-2,1)\text{,}\) \(B=(4,7)\) y \(C=(6,-3)\) los cuales forman el triángulo \(ABC\text{,}\) determine su ortocentro (ortocentro: punto de intersección de las alturas del triángulo \(ABC\)).
\([ Resp.\ \ (\frac{4}{3},\frac{5}{3}) ]\) -
Determine el valor de los coeficientes \(A\) y \(B\) de la ecuación \(Ax-By+4 = 0\) de una recta, si debe pasar por los puntos \((-3,1)\) y \((1,6)\text{.}\)
\([ Resp.\ \ A = \frac{20}{19} , B= \frac{16}{19} ]\) -
Encuentre los valores de \(k\) para que la reta \(4x+5y+k=0\text{,}\) forme un triángulo rectángulo con los ejes coordenados (eje \(X\) y eje \(Y\)), donde su área sea igual a \(\frac{5}{2}\text{.}\)
\([ Resp.\ \ k = 10 \ o \ k=-10 ]\) -
Determine los valores para \(a\) y \(b\) de tal manera que las rectas \(ax+(2-b)y -23 = 0\) y \((a-1)x+by+15=0\) pasen por el punto \((2,-3)\text{.}\)
\([ Resp.\ \ a=4 , b=7 ]\) -
Hallar la ecuación del lugar geométrico de un punto que se mueve de tal manera que su distancia de la recta \(4x-3y+12=0\) es siempre igual a la mitad de su distancia al eje \(Y\text{.}\)
\([ Resp.\ \ x-2y+8=0 \ o \ 13x-6y+24=0 ]\) -
Calcule la distancia entre las rectas
\begin{equation*} L_{1} : 2x+3y-6=0 \ \ y \ \ L_{2}: 2x+3y+ 13 = 0 \end{equation*}\([ Resp.\ \ \frac{19}{\sqrt{13}} ]\)
