[skip-to-content]

Sección 2.5 Parábola

Definición 2.5.1

Una parábola es el conjunto formado por todos los puntos que se encuentran a la misma distancia de un punto fijo llamado foco y de una recta llamada directriz.

Observación: En este texto solamente se abordaran los casos que la directriz sea paralela al eje \(X\) o al eje \(Y\text{.}\)

Descripción de los puntos que están o pertenecen a la Parábola: Sea \(F \in \mathbb{R}^{2}\) que representa el foco y \(l\) una recta del plano (en el dibujo paralela al eje \(Y\)). Consideremos la recta que pasa por el foco y es perpendicular a \(l\text{,}\) es decir, \(l_{1} \perp l\text{,}\) \(l_{1}\) es llamada eje focal.

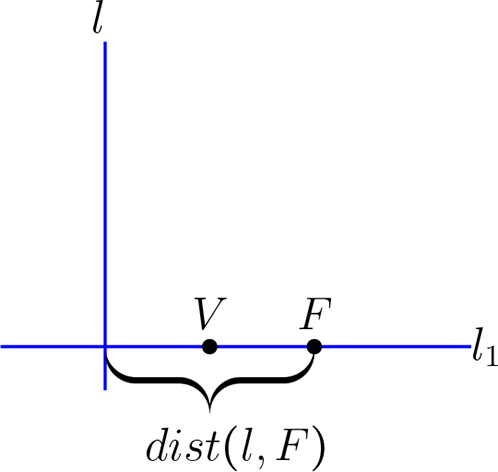
Sea \(r \in \mathbb{R}^{+}\) la distancia que hay entre el foco y la directriz

\begin{equation*} dist(l,F) = r=2p \end{equation*}

Si \(V \in \mathbb{R}^{2}\text{,}\) es el punto medio \(\overline{FP_0}\text{,}\) donde \(P_0\) es el punto de intersección de \(l\) y \(l_{1}\text{,}\) el punto \(V \) anteriormente nombrado lo llamaremos vértice de la parábola y cumple con

\begin{equation*} dist(l,V) = dist(F,V) = \frac{r}{2} = p \end{equation*}

Sea \(P \in \mathbb{R}^{2}\) un punto que pertenece a la parábola, luego

\begin{equation*} dist(l,P) = dist(F,P) \end{equation*}

Así tenemos que la parábola con foco \(F\) y directriz \(l\) es:

\begin{equation*} \mathcal{P}_{(l,F)} = \{ P \in \mathbb{R}^{2} \mid dist(l,P) = dist(F,P) \} \end{equation*}

El cual gráficamente corresponde a la siguiente figura

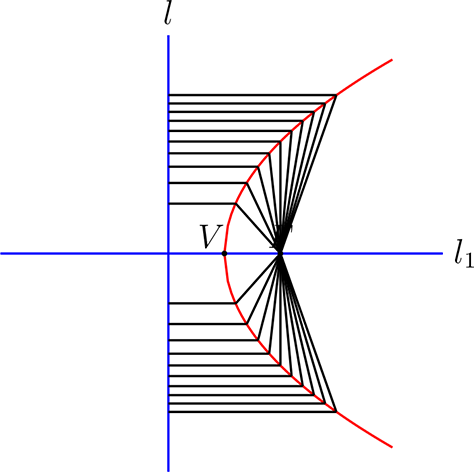
Luego al considerando solamente los puntos, sin marcar las distancias, tenemos la siguiente figura conocida como parábola.

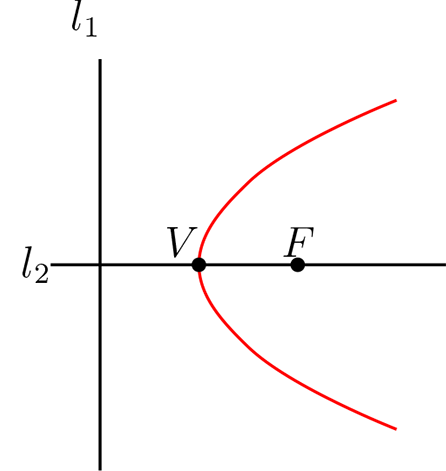
Observación: Note que hemos realizado el proceso en forma general y solamente hemos visualizado una de las cuatro posibilidades de abertura de la Parábola. A continuación detallaremos más cada caso.

Subsección 2.5.1 Ecuación de la parábola con eje focal paralelo al eje X

Sean \(F,V \in \mathbb{R}^{2}\text{,}\) con \(V = (h,k)\) el vértice de la parábola, \(F=(h+p,k)\) el foco y \(l_1: x= h-p\) la directriz.

En este caso, se tiene el eje focal paralelo al eje \(X\text{,}\) luego las gráficas que nos encontramos en este caso son las siguientes:

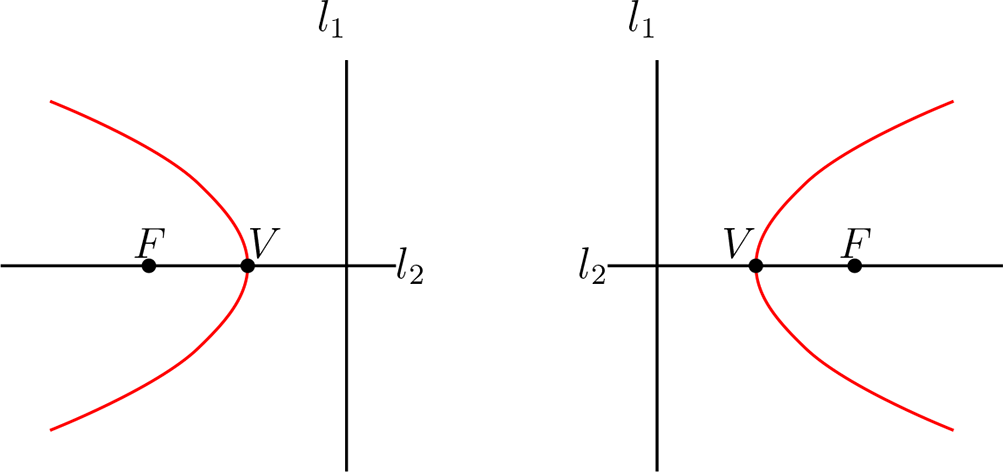
Sea \(P=(x,y)\) un punto de la parábola, luego la distancia es

\begin{equation*} \begin{array}{rcl} dist(l,P) = \frac{\mid 1 \cdot x + 0 \cdot y + p-h \mid}{\sqrt{1^{2} + 0^{2}}} = \mid x + p-h \mid \end{array} \end{equation*}

Además de la distancia entre puntos, obtenemos

\begin{equation*} \begin{array}{rcl} dist(F,P) = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} = \sqrt{(x - (h+p))^{2} + (y-k)^{2}} \end{array} \end{equation*}

Realicemos el cambio de variable \(u=x-h\) y \(v=y-k\text{,}\) en estas coordenadas obtenemos

\begin{equation*} \begin{array}{rcl} \mid u + p \mid \amp =\amp \sqrt{(u - p)^{2} + v^{2}}\\ (u + p)^2 \amp =\amp (u - p)^{2} + v^{2} \\ v^{2} \amp =\amp (u + p)^{2} -(u - p)^2=4pu \end{array} \end{equation*}

Así, tenemos que

\begin{equation*} \begin{array}{rcl} v^{2} \amp =\amp 4pu, \end{array} \end{equation*}

volviendo a las coordenadas originales

\begin{equation*} \begin{array}{rcl} (y-k)^{2} \amp =\amp 4p (x-h) \end{array} \end{equation*}

Encuentre la ecuación de la parábola, la directriz, el foco si esta tiene como vértice \((0,0)\text{,}\) pasa por el punto \((4,-3)\) y el eje focal está en el eje \(X\text{.}\)

Solución 1

Como la parábola tiene su vértice en el origen \((h,k)=(0,0)\text{,}\) tenemos que su ecuación esta dada por:

\begin{equation*} \begin{array}{rcl} y^{2} = 4px \end{array} \end{equation*}

Pero además, pasa por el punto \((4,-3)\text{,}\) el cual debe satisfacer la ecuación \(y^{2} = 4px \text{,}\) reemplazando se obtiene

\begin{equation*} \begin{array}{rcl} (-3)^{2} \amp =\amp 4p \cdot 4 \\ p \amp =\amp \frac{9}{16} \end{array} \end{equation*}

Luego, el foco esta dado por el punto \((p,0)\) lo que corresponde a \((\frac{9}{16},0)\text{.}\) Finalmente la directriz tiene ecuación \(l:x=-p\text{,}\) es decir,

\begin{equation*} l: x =- \frac{9}{16} \end{equation*}

Y de este modo la ecuación es

\begin{equation*} y^{2} = \frac{9}{4}x \end{equation*}

Encuentre la ecuación de la parábola, la directriz y su foco si el vértice es \((6,2)\text{,}\) pasa por el punto \((-3,5)\) y el eje focal es paralelo al eje \(X\text{.}\)

Solución 2

Como la parábola tiene su vértice en el punto \((6,2)\) tenemos que su ecuación esta dada por:

\begin{equation*} \begin{array}{rcl} (y - k)^{2} \amp =\amp 4p(x-h) \\ (y-2)^{2} \amp =\amp 4p(x-6) \end{array} \end{equation*}

Además, pasa por el punto \((-3,5)\) el cual debe satisfacer la ecuación

\begin{equation*} \begin{array}{rcl} (y - 2)^{2} \amp =\amp 4p(x-6) \\ (5-2)^{2} \amp =\amp 4p \cdot (-3-6) \\ 9 \amp =\amp -36p \\ p \amp =\amp \frac{-1}{4} \end{array} \end{equation*}

Luego el foco esta dado por el punto

\begin{equation*} \begin{array}{rcl} (h+p,k)=\left(6+\frac{-1}{4},2\right) = \left(\frac{23}{4},2\right) \end{array} \end{equation*}

Finalmente la ecuación de la directriz \(l: x = h-p\) es

\begin{equation*} l: x = 6 - \frac{-1}{4} = \frac{25}{4} \end{equation*}

Y de este modo la ecuación de la parábola es

\begin{equation*} (y-2)^{2} = -(x-6) \end{equation*}

Subsección 2.5.2 Ecuación de la parábola con eje focal paralelo al eje Y

Sea \(F,V \in \mathbb{R}^{2}\text{,}\) con \(V = (h,k)\) el vértice de la parábola, \(F =(h,k+p)\) el foco y \(l_1: y=k-p\) la directriz.

En este caso, se tiene el eje focal paralelo al eje \(Y\text{,}\) luego las gráficas que nos encontramos en este caso son las siguientes:

Sea \(P=(x,y)\) un punto de la parábola, luego las distancia son:

\begin{equation*} \begin{array}{rcl} dist(l,P) = dist(F,P) \end{array} \end{equation*}

Usando la formula de distancia punto a recta tenemos

\begin{equation*} \begin{array}{rcl} dist(l,P) = \frac{\mid 0 \cdot x + 1 \cdot y + p-k \mid}{\sqrt{0^{2} + 1^{2}}} = \mid y + p-k \mid \end{array} \end{equation*}

Ahora la de distancia entre puntos tenemos

\begin{equation*} \begin{array}{rcl} dist(F,P) = \sqrt{(x - h)^{2} + (y - (k+p))^{2}} = \sqrt{(x-h)^{2} + (y-k-p)^{2}} \end{array} \end{equation*}

Por lo tanto como

\begin{equation*} \begin{array}{rcl} dist(l,P) \amp = \amp dist(F,P) \\ \mid y + p-k \mid \amp = \amp \sqrt{(x-h)^{2} + (y-k-p)^{2}} \end{array} \end{equation*}

Volvemos a hacer cambio de variable \(u=x-h\) y \(v=y-k\text{,}\) luego tenemos que

\begin{equation*} \begin{array}{rcl} \mid v+ p \mid \amp =\amp \sqrt{u^{2} + (v-p)^{2}} \hspace{2cm} /()^{2}\\ ( v+ p)^2 \amp =\amp u^{2} + (v-p)^{2} \\ u^{2} \amp =\amp (v-p)^{2}-(v+ p)^2=4pv \end{array} \end{equation*}

Así entonces tenemos

\begin{equation*} u^{2}= 4pv \end{equation*}

volviendo a las coordenadas originales obtenemos

\begin{equation*} (x - h)^{2} = 4p(y-k) \end{equation*}

Encuentre la ecuación de la parábola, la directriz, su foco si esta tiene como vértice \((0,0)\text{,}\) pasa por el punto \((4,-3)\) y el eje focal es el eje \(Y\text{.}\)

Solución 1

Como la parábola tiene su vértice en el origen \((h,k)=(0,0)\text{,}\) se tiene que su ecuación esta dada por:

\begin{equation*} \begin{array}{rcl} x^{2} = 4py \end{array} \end{equation*}

Pero además pasa por el punto \((4,-3)\) el cual satisface la ecuación, reemplazando se tiene

\begin{equation*} \begin{array}{rcl} (4)^{2} \amp =\amp 4p \cdot -3 \\ p \amp =\amp \frac{-3}{4} \end{array} \end{equation*}

Luego el foco esta dado por el punto \((0,p)\) lo que corresponde a \((0,\frac{-3}{4})\text{.}\) Finalmente la directriz tiene ecuación \(l:y=-p\)

\begin{equation*} \begin{array}{rcl} l:y \amp =\amp \frac{3}{4} \end{array} \end{equation*}

Y de este modo la ecuación de la parábola es

\begin{equation*} x^{2} =-3 y \end{equation*}

Encuentre la ecuación de la parábola, la directriz y su foco si el vértice es \((6,2)\text{,}\) pasa por el punto \((-3,5)\) y si su eje focal es paralelo al eje \(Y\text{.}\)

Solución 2

Como la parábola tiene su vértice es \((h,k)=(6,2)\) y el eje focal es paralelo al eje \(X\text{,}\) se tiene que la ecuación esta dada por:

\begin{equation*} \begin{array}{rcl} (x-h)^{2} \amp =\amp 4p(y-k) \\ (x-6)^{2} \amp =\amp 4p \cdot (y-2) \\ \end{array} \end{equation*}

Pero además pasa por el punto \((-3,5)\text{,}\) es decir, satisface la ecuación

\begin{equation*} \begin{array}{rcl} (-3-6)^{2} \amp =\amp 4p \cdot (5-2) \\ (-9)^{2} \amp =\amp 4p \cdot 3 \\ p \amp =\amp \frac{27}{4} \\ \end{array} \end{equation*}

Luego el foco esta dado por el punto \((h,k+p)\) lo que corresponde a \((6,2+\frac{27}{4})=(6,\frac{35}{4})\text{.}\) Finalmente la directriz tiene ecuación \(l: y = k-p\)

\begin{equation*} \begin{array}{rcl} l:y \amp =\amp 2- \frac{27}{4} = \frac{19}{4} \end{array} \end{equation*}

Y de este modo la ecuación de la parábola es

\begin{equation*} (x-6)^{2} = 27(y-2) \end{equation*}

Observación: El concepto de recta tangente a una parábola en un punto perteneciente a ella, es una recta que pasa por el punto y todos los otros puntos de la parabola perteneces al mismo semiplano que se obtiene con esta recta. Recuerde que toda recta divide al plano en dos semiplano.

Se define el lado recto de una parábola, como el segmento de recta que une los puntos que intercepta la recta paralela a la directriz y que pasa por el foco, como en la figura

Resumen: Dada una parábola, sean \(V,F,A_{1},A_{2} \in \mathbb{R}^{2}\text{,}\) donde \(F=(a,b),\) \(V = (h,k),\) \(A_{1}=(a_{1},b_{1}),\) \(A_{2}=(a_{2},b_{2})\) y \(l,l_{1}\) rectas del plano cartesiano. Los distintos elementos de una parábola distribuidos de la siguiente forma en la figura

  1. Parábola con eje focal paralelo al eje \(X\text{.}\)

    1. El Vértice de la parábola está dado por \(V =(h,k) \)

    2. El Foco de la parábola está dado por \(F =(h+p,k) \)

    3. La Directriz de la parábola está dado por \(l: x= h-p \)

    4. El Eje Focal de la parábola está dado por \(l_{1}: y=k\)

    5. El Lado Recto de la parábola \(\overline{A_{1}A_{2}}\) mide \(4|p| \)

    6. La ecuación de la parábola está dado por \((y-k)^{2} = 4p(x-h) \)

    7. La ecuación de la recta tangente a la parábola en el punto \((a,b)\text{,}\) está dado por \(y-b = \frac{2p}{b-k}(x-a) \text{,}\) con \(b\neq k\)

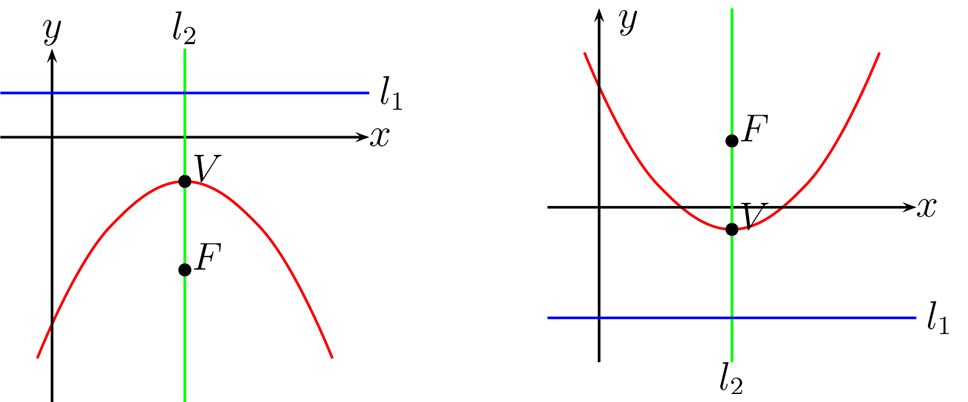
  2. Parábola con eje focal paralelo al eje \(Y\text{.}\)

    1. El Vértice de la parábola está dado por \(V =(h,k) \)

    2. El Foco de la parábola está dado por \(F =(h,k+p) \)

    3. La Directriz de la parábola está dado por \(l: y= h-p \)

    4. El Eje Focal de la parábola está dado por \(l_{1}: x=h\)

    5. El Lado Recto de la parábola \(\overline{A_{1}A_{2}}\) mide \(4|p| \)

    6. La ecuación de la parábola está dado por \((x-h)^{2} = 4p(y-k) \)

    7. La ecuación de la recta tangente a la parábola en el punto \((a,b)\) está dado por \(y-b = \frac{a-h}{2p}(x-a) \text{.}\)

Encuentre la ecuación de la parábola de vértice \(V=(2,3)\text{,}\) foco en la recta \(7x+3y-4=0\) y eje focal horizontal.

Solución 3

Como la parábola tiene su vértice \(V=(2,3)=(h,k)\) y eje focal horizontal su ecuación esta dada por:

\begin{equation*} \begin{array}{rcl} (y-k)^{2} \amp =\amp 4p(x-h) \\ (y-3)^{2} \amp =\amp 4p(x-2) \end{array} \end{equation*}

Ya que el foco esta dado por \(F=(h+p,k)\) entonces

\begin{equation*} F=(2+p,3) \end{equation*}

además el foco \(F\) está en la recta, luego satisface la ecuación \(7x+3y=4\text{,}\) reemplazando obtenemos

\begin{equation*} \begin{array}{rcl} 7(2+p)+3 \cdot 3\amp =\amp 4 \\ 14+7p+9 \amp =\amp 4 \\ 7p\amp =\amp -19 \\ p \amp =\amp \frac{-19}{7} \end{array} \end{equation*}

Por lo tanto el foco de la parábola es

\begin{equation*} F=(2+ \frac{-19}{7},3)=(\frac{-5}{7},3) \end{equation*}

y su ecuación es

\begin{equation*} \begin{array}{rcl} (y-3)^{2}\amp =\amp 4p(x-2) \\ (y-3)^{2}\amp =\amp 4 \left(\frac{-19}{7}\right)(x-2) \end{array} \end{equation*}

Observación: La ecuación general de la parábola esta dada por

  1. Consideremos la ecuación de la parábola con eje focal paralelo al eje \(X\text{.}\)

    \begin{equation*} \begin{array}{rcl} (y - k)^{2} \amp =\amp -4p(x-h) \\ y^{2} - 2ky + k^{2} \amp =\amp -4px + 4ph \\ y^{2} - 2ky +4px + k^{2} - 4 ph \amp =\amp 0 \end{array} \end{equation*}

    Definamos las constantes

    \begin{equation*} \begin{array}{rcl} A_{1} = -2k, \quad B_{1} = 4p, \quad C_{1} = k^{2} - 4ph. \end{array} \end{equation*}

    Reemplazando obtenemos la ecuación

    \begin{equation*} y^{2} + A_{1}y + B_{1}x + C_{1} = 0 \end{equation*}

  2. Ahora consideremos la ecuación de la parábola con eje focal paralelo al eje \(Y\)

    \begin{equation*} \begin{array}{rcl} (x-h)^{2} \amp =\amp 4p(y-k) \\ x^{2} - 2xh + h^{2} \amp =\amp 4py - 4pk \\ x^{2} - 2hx - 4py +h^{2} +4pk \amp =\amp 0 \end{array} \end{equation*}

    Definimos las constantes

    \begin{equation*} \begin{array}{rcl} A_{2} = -2h, \quad B_{2} = -4p, \quad C_{2} = h^{2} + 4pk. \end{array} \end{equation*}

    Reemplazando obtenemos

    \begin{equation*} x^{2} + A_{2}x + B_{2}y + C_{2} = 0 \end{equation*}

Considere la ecuación de la parábola \(2x^{2}+5x+y-13=0\text{.}\) Encuentre toda los elementos distinguidos de la parábola.

Solución 4

Para determinar los elementos, completaremos cuadrado, para ello tenemos que la ecuación de la parábola

\begin{equation*} \begin{array}{rcl} 2x^{2}+5x+y-13\amp =\amp 0 \\ 2x^{2}+5x \amp =\amp -y+13 \ \ / \cdot \frac{1}{2} \\ \left(x^{2}+ \frac{5}{2}x\right) \amp =\amp \frac{-y}{2} + \frac{13}{2} \ / +\frac{25}{16} \\ \left(x^{2}+ \frac{5}{2}x+\frac{25}{16}\right) \amp =\amp \frac{-y}{2} + \frac{13}{2}+\frac{25}{16} \\ \left(x + \frac{5}{4}\right)^{2} \amp =\amp \frac{-y}{2} + \frac{129}{16} \\ \left(x + \frac{5}{4}\right)^{2} \amp =\amp \frac{-1}{2}\left(y- \frac{129}{8}\right) \end{array} \end{equation*}

Luego \(4p=-\frac{1}{2}\) entonces \(p=-\frac{1}{8}\text{.}\)

Por lo tanto el vértice de la parábola esta dado por

\begin{equation*} V=(h,k)=\left(\frac{-5}{4},\frac{129}{8}\right) \end{equation*}

El foco dado por

\begin{equation*} F=(h,k+p)=\left(\frac{-5}{4},\frac{129}{8}-\frac{1}{8}\right)=\left(\frac{-5}{4}, \frac{128}{8}\right)=\left(\frac{-5}{4},16\right) \end{equation*}

La directriz de la parábola tiene como ecuación

\begin{equation*} \begin{array}{rcl} l\amp :\amp y= k-p = \frac{129}{8}-\frac{-1}{8} = \frac{130}{8} = \frac{65}{4} \end{array} \end{equation*}

El eje focal es

\begin{equation*} \begin{array}{rcl} x\amp =\amp \frac{-5}{4} \end{array} \end{equation*}

Y el lado recto mide

\begin{equation*} \begin{array}{rcl} 4p\amp =\amp \frac{1}{2} \end{array} \end{equation*}

Subsección 2.5.3 Ejercicios Propuestos

  1. Grafique y encuentre vértice, foco y directriz en las siguientes ecuaciones.

    1. \(y^{2}-8x-4y+4=0\)
    2. \(y^{2}+8x-4y-28=0\)
    3. \(y^{2}+1=x\)
    4. \(y^{2}-x-6y+11=0\)
    5. \(y^{2}-6x+6y+27+27=0\)
    6. \(x^{2}=-4x-3y-7\)
    7. \(4 y^{2}-48x-20y=71\)

  2. Encuentre el o los puntos de intersección de las siguientes parábolas \(y^{2}-8x-4y+4=0\) e \(y^{2}+8x-4y-28=0\text{.}\)

    [Resp. \((2,-2)\) y \((2,6)\)]

  3. Indique que representa la ecuación \(x^{2}+4x-8y+36=0\text{,}\) grafiquela y encuentre todas sus componentes.

  4. Determinar la ecuación de la parábola cuya directriz pasa por \((-3,0)\) con vértice en el origen.

    [Resp. \(y^{2}=12x\)]

  5. Encuentre la ecuación de la directriz de la parábola \(y=2x^{2}\text{.}\)

    [Resp. \(y= \frac{-1}{8}\)]

  6. Hallar la ecuación de la parábola cuyo eje paralelo al eje \(X\) y que pasa por los tres puntos \((0,0)\) , \((8,-4)\) y \((3,1)\text{.}\)

    [Resp. \(y^{2}-x+2y=0\) ]

  7. Hallar la ecuación de la parábola de vértice el punto \((4,-1)\text{,}\) eje la recta \(y+1=0\) y que pasa por el punto \((3,-3)\text{.}\)

    [Resp. \(y^{2}+4x+2y-15=0\) ]

  8. Hallar e identificar la ecuación del lugar geométrico de un punto que se mueve de tal manera que su distancia de la recta \(x+3=0\) es siempre 2 unidades mayor que su distancia del punto \((1,1)\text{.}\)

    [Resp. \(y^{2}-4x-2y+1=0\) ]

  9. Hallar e identificar la ecuación del lugar geométrico de centro de una circunferencia que es siempre tangente a la recta \(y-1=0\) y a la circunferencia \(x^{2}+y^{2}=9\text{.}\)

    [Resp. \(x^{2}-4y-4=0\) o bien \(x^{2}+8y-16=0\) ]

  10. Hallar la ecuación de la tangente a la parábola \(x^{2}+4x+12y-8=0\) que es paralela a la recta \(3x+9y-11=0\text{.}\)

    [Resp. \(x+3y-2=0\) ]

  11. Hallar las ecuaciones de las tangentes trazadas del punto \((1,4)\) a la parábola \(y^{2}-3x-8y+10=0\text{.}\)

    [Resp. \(x+2y-9 = 0\) o \(3x-2y+5=0\) ]

  12. Determine la ecuación de la recta que es tangente a la parábola \(x^{2}=-5y\) en el punto \((5,-5)\text{.}\)

    [Resp. \(L:y=-2x+5\)]

  13. Hallar la ecuación de las tangentes a la parábola \(y^{2}+3x-6y+9=0\) y que pasa por el punto \((1,4)\)

    [Resp. \(L_{1}:2y=-x+9\text{,}\) \(\quad L_{2}: 2y=3x+5\)]