Sección 3.2 Relaciones de Orden
¶
Definición 3.2.1
Sea \(\mathcal{R}\) una relación en \(A\text{.}\)
Se dice que \(\mathcal{R}\) es una relación de orden en \(A\) o \(\mathcal{R}\) es un orden en \(A\) si y sólo si \(\mathcal{R}\) es una relación refleja, antisimétrica y transitiva en \(A\text{.}\)
Se llama conjunto ordenado al par \((A, \mathcal{R})\text{,}\) donde \(\mathcal{R}\) es una relación de orden en \(A\text{.}\)
Dados dos conjuntos ordenados \((A,\mathcal{R})\) y \((A^{\prime}
,\mathcal{R}^{\prime})\) son iguales si y sólo si se cumple que \(A=A^{\prime}\) y que \(\mathcal{R}=\mathcal{R}^{\prime}\text{.}\)
-
Se dice que \(\mathcal{R}\) es una relación de orden total en \(A\) o que \((A,\mathcal{R})\) es un conjunto totalmente ordenado si y sólo si cumple
\(\mathcal{R}\) es una relación de orden en \(A\)
-
\(\mathcal{R}\) es una relación total en \(A\text{,}\) es decir,
\begin{equation*}
(\forall a,b\in A)(a\mathcal{R}b\vee b\mathcal{R}a)
\end{equation*}
Ejemplo 3.2.2
El conjunto \((\mathbb{R},\ \leq)\) es un orden total pues:
Es Refleja: \((\forall x\in\mathbb{R})(x\leq x)\text{.}\)
Es Antisimétrica: \((\forall x,y\in\mathbb{R})[(x\leq y\wedge
y\leq x)\Rightarrow x=y]\text{.}\)
Es Transitiva: \((\forall x,y,z\in\mathbb{R})[(x\leq y\wedge
y\leq x)\Rightarrow x\leq z]\text{.}\)
Es Total: \((\forall x,y\in\mathbb{R})(x\leq y\vee y\leq x)\text{,}\) es decir en \(\mathbb{R}\) siempre se pueden comparar dos elementos.
Ejemplo 3.2.3
Sean \(E\) una conjunto no vacío y \(\mathcal{P}(E)\) el conjunto potencia, luego \((\mathcal{P}(E),\subseteq)\text{,}\) es un conjunto ordenado pero en general el orden no es total.
-
Refleja:
\begin{equation*}
(\forall A\in\mathcal{P}(E))\left( A\subseteq A\right)
\end{equation*}
-
Antisimétrica:
\begin{equation*}
(\forall A,B\in\mathcal{P}(E))\left[ \left( A\subseteq B\wedge
B\subseteq A\right) \Longrightarrow A=B\right]
\end{equation*}
-
Transitiva:
\begin{equation*}
(\forall A,B,C\in\mathcal{P}(E))\left[ \left( A\subseteq B\wedge
B\subseteq C\right) \Longrightarrow A\subseteq C\right]
\end{equation*}
por lo tanto, \(\subseteq \) es una relación de orden.
Ejemplo 3.2.4
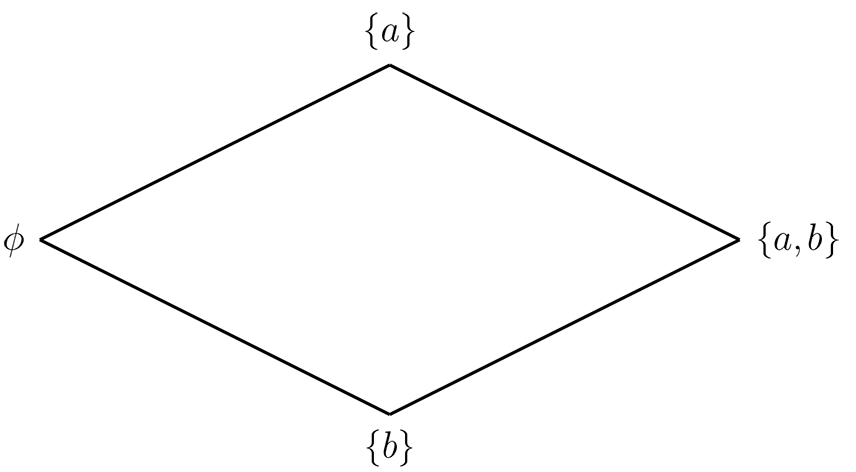
Un caso particular del caso anterior, lo tenemos con \(E=\{a,b\}\text{,}\) y sea \(\mathcal{P}(E)=\{\phi,\{a\},\{b\},\{a,b\}\}\text{,}\) considere el conjunto \((\mathcal{P}(E),\subseteq)\text{,}\) luego tenemos el siguiente diagrama
Tenemos que \(\subseteq\) es refleja antisimétrica y transitiva pero no total, pues
\begin{equation*}
\{a\}\nsubseteq\{b\}\vee\{b\}\nsubseteq\{a\}
\end{equation*}
por lo cual la proposición
\begin{equation*}
(\forall A,B\in\mathcal{P}(E))\left[ A\subseteq B\vee B\subseteq A\right]
\end{equation*}
es falsas.
Subsección Ejercicios
Sea \(\mathcal{R}=\{(x,y)\in\mathbb{N}\times\mathbb{N}\mid
x^{2}+x\leq y^{2}+y\}\text{.}\)
Demostrar que \(\mathcal{R}\) es una relación de orden en \(\mathbb{N}\text{.}\)
Definición 3.2.5
Sean \(\mathcal{R}\) una relación de orden en \(A\text{,}\) n \(a \in A\) y \(X\subseteq A\text{,}\) entonces
-
Elemento maximal.
Se dice que \(a\) es el elemento maximal de \((A,\ \mathcal{R})\) si y sólo si
\begin{equation*}
(\forall x\in A)(a\mathcal{R}x\Rightarrow a=x).
\end{equation*}
-
Elemento minimal.
Se dice que \(a\) es el elemento minimal de \((A,\ \mathcal{R})\) si y sólo si
\begin{equation*}
(\forall x\in A)(x\mathcal{R}a\Rightarrow x=a).
\end{equation*}
-
Primer elemento.
Se dice \(a\) es el primer elemento de \((A, \ \mathcal{R})\) si y sólo si
\begin{equation*}
(\forall x\in A)(a\mathcal{R}x).
\end{equation*}
-
Último elemento.
Se dice \(a\) es el último elemento de \((A, \ \mathcal{R})\) si y sólo si
\begin{equation*}
(\forall x\in A)(x\mathcal{R}a).
\end{equation*}
-
Cota superior.
Se dice que \(a\) es cota superior de \(X\) si y sólo si
\begin{equation*}
(\forall x\in X)(x\mathcal{R}a).
\end{equation*}
-
Cota inferior.
Se dice que \(a\) es cota inferior de \(X\) si y sólo si
\begin{equation*}
(\forall x\in X)(a\mathcal{R}x).
\end{equation*}
Ejemplo 3.2.6
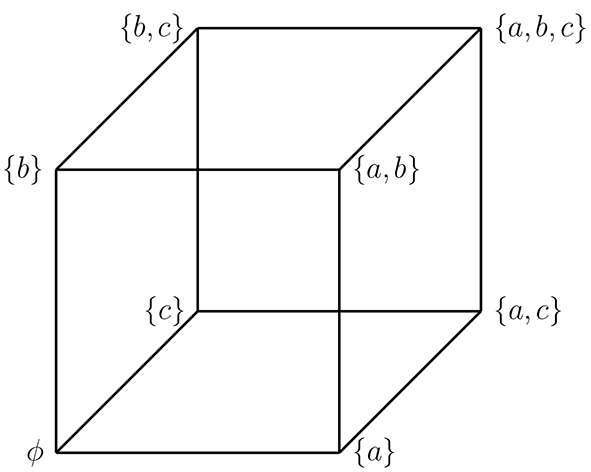
Sea \(E=\{a,b,c\}\text{,}\) y consideraremos a \((\mathcal{P}(E),\subseteq)\text{.}\)
Tenemos que
\begin{equation*}
\mathcal{P}(E)=\{\phi,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}\},
\end{equation*}
mediante el siguiente diagrama podemos ilustrar las contenciones que encontraremos en \(\mathcal{P}(E)\text{.}\)
Luego el elemento maximal es \(E\text{,}\) pues
\begin{equation*}
\begin{array}
[c]{c}
(\forall B\in\mathcal{P}(E))(E\subseteq B\Rightarrow E=B)\\
E\subseteq B\wedge B\in\mathcal{P}(E)\\
E\subseteq B\wedge B\subseteq E\\
E=B.
\end{array}
\end{equation*}
Por otra parte el elemento minimal es \(\phi\text{,}\) ya que
\begin{equation*}
(\forall B\in\mathcal{P}(E))(B\subseteq\phi\Rightarrow B=\phi).
\end{equation*}
Subsección Ejercicios
Sea \(A=\{(1,2),(1,4),(2,3),(2,1)\}\text{,}\) luego definimos la siguiente relación
\begin{equation*}
(x,y)\mathcal{R}(x^{\prime},y^{\prime})\Leftrightarrow\lbrack x\lt x^{\prime}
\vee(x=x^{\prime}\wedge y^{\prime}\leq y)],
\end{equation*}
donde \((A,\mathcal{R})\) es un conjunto ordenado.
Determinar primer elemento, último elemento, elemento maximal, elemento minimal.
Observación: Recuerde que si un conjunto \(A\) posee una propiedad universal \(P\) y \(B\subseteq A\text{,}\) entonces la propiedad \(P\) se cumple en el subconjunto \(B\text{.}\)
Definición 3.2.7
Se dice que un conjunto ordenado \((A,\ \mathcal{R})\) esta bien ordenado si y sólo si todo subconjunto ordenado de \((A,\mathcal{R})\text{,}\) no vacío tiene primer elemento. En este caso, también se dice que \(\mathcal{R}\) es un buen orden en \(A\text{.}\)
Ejemplo 3.2.8
Sea \((\mathbb{N},\leq)\) es un conjunto bien ordenado.
Ejemplo 3.2.9
\((\mathbb{Z},\leq)\) no es un conjunto bien ordenado.
Ejemplo 3.2.10
Sea \(E=\{a,b,c\}\text{,}\) donde \((\mathcal{P}(E),\subseteq)\text{,}\) consideraremos el conjunto
\begin{equation*}
A=\{\{a\},\{b\},\{a,c\}\}\subseteq\mathcal{P}(E),
\end{equation*}
luego \((A,\subseteq)\) no tiene primer elemento, por tanto \((\mathcal{P}
(E),\ \subseteq)\) no es un conjunto bien ordenado.
Proposición 3.2.11
Sea \({\cal R}\) una relación de orden en \(A\text{.}\)
Si \({\cal R}\) es un buen orden en \(A\) entonces \({\cal R}\) es orden total en \(A\)
Demostración
Sean \(a,b \in A\text{,}\) luego \(\{a,b \}
\subseteq A\text{,}\) por lo tanto \(\{a,b \}\) tiene primer elementos.
Si \(a\) es el primer elemento de \(\{a,b \}\) luego
\begin{equation*}
a{\cal R} b
\end{equation*}
Si \(b\) es el primer elemento de \(\{a,b \}\text{,}\) luego
\begin{equation*}
b {\cal R} a
\end{equation*}
Por lo tanto
\begin{equation*}
a{\cal R} b \ \ \ \vee \ \ \ b {\cal R} a
\end{equation*}
Observación: No todos los ordenes totales son buen orden, para ello tenemos.
\(\leq \) no es un buen orden en \(\mathbb{Z}\)
\(\leq \) no es un buen orden en \(]0,\infty[\)
\(\leq \) no es un buen orden en \([0,\infty[\)
Axioma de Elección
Todo producto cartesiano de una familia no vacía de conjunto no vacío es no vacía.
Observación: El anterior axioma nos dice que dado \(\{A_i\}_{i\in I}\) una familia no vacía \(I\not =\phi \) de conjunto y los conjuntos son no vacíos \((\forall i\in
I)(A_{i}\not =\phi)\text{,}\) entonces
\begin{equation*}
\underset{i\in I}{\times} A_i \not =\phi.
\end{equation*}
Teorema 3.2.12 [Zermelo]
Si \(A\) es un conjunto no vacío, entonces existe una relación sobre \(A\) que es un buen orden.
Teorema 3.2.13 [Lema Zorn]
Sea \((A,\mathcal{R})\) un conjunto ordenado inductivo (es decir, si \(C\subseteq A\) no vacío, totalmente ordenado entonces \(C\) tiene cota superior). Entonces \(A\) tiene un elemento maximal.