Sección 4.3 Forma Polar de un Complejo
¶Ahora veremos un interpretación del módulo, para ellos sea \(z=a+bi\text{,}\)
>Todo numero complejos \(z\) es el par ordenado \((a,b)\text{,}\) luego el módulo de \(z\) es la distancia desde el origen al punto \((a,b)\text{.}\)
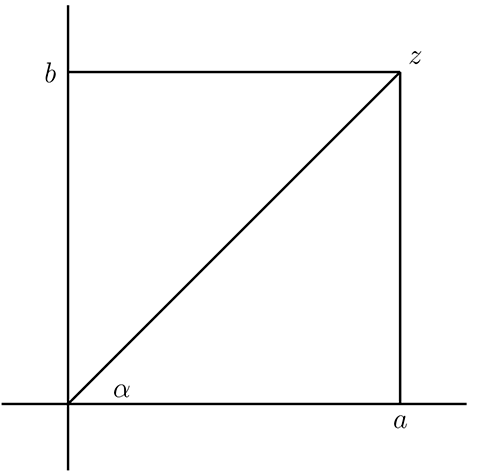
Sea \(z=a+bi\text{,}\) luego tenemos el siguiente gráfico
Recordando que
\(\operatorname{cos}(\alpha)=\frac{{\text{cat ady}}}{\text{hip}}\text{.}\)
Lo que es equivalente a decir:
\begin{equation*}
\operatorname{cos}(\alpha)=\frac{\operatorname{Re}(z)}{|z|}.
\end{equation*}
\(\operatorname{sen}(\alpha)=\frac{{\text{cat op}}}{\text{hip}}\text{.}\)
Lo que es equivalente a:
\begin{equation*}
\operatorname{sen}(\alpha)=\frac{\operatorname{Im}(z)}{|z|}.
\end{equation*}
La forma polar de un complejo \(z=a+bi\) esta dada por:
\begin{equation*}
z=|z|\operatorname{cos}(\alpha)+(|z|\operatorname{sen}(\alpha))i=|z|[\operatorname{cos}\alpha+i\operatorname{sen}\alpha].
\end{equation*}
Notación:
\begin{equation*}
\operatorname{cos}(\alpha)+i \operatorname{sen}(\alpha)= cis(\alpha)
\end{equation*}
Ejemplo 4.3.1
Transformar a su forma polar
\(z=i=|i|cis(\pi/2)=cis(\pi/2)\text{.}\)
\(z=3cis(\pi/4)=3\operatorname{cos}(\pi/4)+3i\operatorname{sen}(\pi/4)=\frac{3\sqrt{2}}{2}+\frac{3\sqrt
{2}}{2}i\text{.}\)
Ejemplo 4.3.2
Calcular en forma polar
- \(|cis\alpha|=|\operatorname{cos}\alpha+i\operatorname{sen}\alpha
|=\sqrt{\operatorname{cos}^{2}\alpha+\operatorname{sen}^{2}\alpha}=1.\)
- \((cis\alpha)^{-1}=cis(-\alpha).\)
Propiedades:
Consideremos \(z= |z| cis(\alpha), w= |w|cis(\beta)\in\mathbb{C}\text{,}\) entonces se cumple
\(z\cdot w=|z\cdot w|cis(\alpha+\beta)\text{.}\)
\(z:w=\left| \frac{z}{w}\right| cis(\alpha-\beta)\text{,}\) con \(w\not =0\text{.}\)
\(z^{n}=|z|^{n}cis(n\alpha)\text{,}\) \(n\in\mathbb{N}\text{.}\)
Observación:Recordemos alguna identidades trigonometrías básicas
\(\operatorname{cos}(\alpha\pm\beta)=\operatorname{cos}\alpha\operatorname{cos}\beta\mp\operatorname{sen}
\alpha\operatorname{sen}\beta\text{.}\)
\(\operatorname{sen}(\alpha\pm\beta)=\operatorname{sen}\alpha\cos\beta
\pm\operatorname{sen}\beta\cos\alpha\text{.}\)
\(\cos(\alpha)=\cos(-\alpha)\text{.}\)
\(\operatorname{sen}(-\alpha)=-\operatorname{sen}(\alpha)\text{.}\)
-
\(\cos(\alpha+2k\pi)=\cos(\alpha)\text{.}\)
\(\operatorname{sen}(\alpha+2k\pi)=\operatorname{sen}(\alpha)\text{,}\) \(k\in\mathbb{Z}\)
Demostración
La multiplicación compleja en forma binomial
\begin{equation*}
\begin{array}{rl}
(cis\alpha)\cdot(cis\beta) \amp =(\cos\alpha+i\operatorname{sen}\alpha
)(\cos\beta+i\operatorname{sen}\beta)\\
\amp =\cos\alpha\cos\beta-\cos\alpha\operatorname{sen}\beta+i\operatorname{sen}
\alpha\cos\beta-i\operatorname{sen}\beta\operatorname{sen}\alpha\\
\amp =\left[ \cos\alpha\cos\beta-\operatorname{sen}\alpha\operatorname{sen}
\beta\right] +i[\cos\alpha\operatorname{sen}\beta+\operatorname{sen}
\alpha\cos\beta]\\
\amp =\cos(\alpha+\beta)+i\operatorname{sen}(\alpha+\beta)\\
\amp =cis(\alpha+\beta).
\end{array}
\end{equation*}
Luego
\begin{equation*}
\begin{array}{rl}
z\cdot w \amp =|z|cis(\alpha)\cdot|w|cis(\beta)\\
\amp =|z||w|cis(\alpha)cis(\beta)\\
\amp =|zw|cis(\alpha+\beta)
\end{array}
\end{equation*}
Además notemos que
\begin{equation*}
\begin{array}{rl}
\overline{cis}(\alpha) \amp =\overline{\cos\alpha+i\operatorname{sen}\alpha}\\
\amp =\cos\alpha-i\operatorname{sen}\alpha\\
\amp =\cos(-\alpha)+i\operatorname{sen}(-\alpha)\\
\amp =cis(-\alpha)
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{rl}
z\div w \amp =|z|cis(\alpha)\div|w|cis(\beta)\\
\amp =|z|cis(\alpha)\cdot\frac{1}{|w|}\overline{cis(\beta)}\\
\amp =|z|\cdot\frac{1}{|w|}cis(\alpha)cis(-\beta)\\
\amp =\left| \frac{z}{w}\right| cis(\alpha-\beta)
\end{array}
\end{equation*}
Ejemplo 4.3.3
Calcular \((1-i)^{50}\text{.}\)
Reescribiendo en forma polar el número complejo tenemos
\begin{equation*}
1-i=\sqrt{2}cis(-\pi/4),
\end{equation*}
Aplicando la propiedad
\begin{equation*}
\begin{array}{rl}
(1-i)^{50} \amp =(\sqrt{2})^{50}cis\left( \frac{-50\pi}{4}\right) \\
\amp =(2)^{25}cis\left( \frac{-25\pi}{2}\right) \\
\amp =(2)^{25}cis\left( -(\pi/2+12\pi)\right) \\
\amp =(2)^{25}\overline{cis(\pi/2)}\\
\amp =(2)^{25}[\overline{0+i}]\\
\amp =-2^{25}i.
\end{array}
\end{equation*}
Ejemplo 4.3.4
Simplificar
\begin{equation*}
A=\frac{\left( 1+i\right) ^{20}\left( \sqrt{3}+i\right) ^{18}}{\left(
\sqrt{3}i+1\right) ^{24}}
\end{equation*}
Transformando a la forma polar tenemos que
\begin{equation*}
\begin{array}{rl}
A \amp =\frac{\left( 1+i\right) ^{20}\left( \sqrt{3}+i\right) ^{18}
}{\left( \sqrt{3}i+1\right) ^{24}}\\
A \amp =\frac{\left( \sqrt{2}cis\left( \frac{\pi}{4}\right) \right)
^{20}\left( 2cis\left( \frac{\pi}{6}\right) \right) ^{18}}{\left(
2cis\left( \frac{\pi}{3}\right) \right) ^{24}}\\
A \amp =\frac{2^{10}cis\left( \frac{20\pi}{4}\right) 2^{18}cis\left(
\frac{18\pi}{6}\right) }{2^{24}cis\left( \frac{24\pi}{3}\right) }\\
A \amp =2^{4}cis\left( \frac{20\pi}{4}+\frac{18\pi}{6}-\frac{24\pi}{3}\right)
\\
A \amp =2^{4}cis\left( 5\pi+3\pi-8\pi\right) =2^{4}cis\left( 0\right)
=2^{4}.
\end{array}
\end{equation*}
Propiedades de la raíz \(n\)-ésima:
Sea \(w\in\mathbb{C}\text{,}\) \(n\in\mathbb{N}^{\ast}\text{,}\) entonces:
\begin{equation*}
z^{n}=w=|w|cis(\alpha),
\end{equation*}
tiene \(n\) soluciones y son
\begin{equation*}
z_{k}= \sqrt[n]{|w|}\cdot cis\left( \frac{\alpha+2k\pi}{n}\right) ,
\quad k\in\mathbb{J}_{n-1}.
\end{equation*}
Ejemplo 4.3.5
Encontrar las soluciones de la ecuación
\begin{equation*}
z^{2}=i=cis(\pi/2),
\end{equation*}
Aplicando la propiedad tenemos
\begin{equation*}
z_{k}=\sqrt{1}cis\left( \frac{\frac{\pi}{2}+2k\pi}{2}\right) ,\quad
k\in\{0,1\},
\end{equation*}
de donde
\begin{equation*}
\begin{array}{rl}
\amp z_{0}\sqrt{1}cis\left( \frac{\pi/2+0}{2}\right) \\
\amp =cis(\pi/4)\\
\amp =\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}.
\end{array}
\end{equation*}
Y
\begin{equation*}
\begin{array}{rl}
z_{1} \amp =\sqrt{1}cis\left( \frac{\pi/2+2\pi}{2}\right) \\
\amp =cis(5\pi/4)\\
\amp =-\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2}.
\end{array}
\end{equation*}
De donde \(z_{0}=-z_{1}.\)
Subsección Ejercicios
Resolver
\begin{equation*}
z^{4}=\frac{\left( 1-i\right) ^{20}\left( \sqrt{3}-i\right) ^{15}}{\left(
1-\sqrt{3}i\right) ^{24}}
\end{equation*}